城市表层土壤重金属污染的分析与评价
成夏炎 张 云
(湖南第一师范学院,长沙 410205)
城市表层土壤重金属污染的分析与评价
成夏炎 张 云
(湖南第一师范学院,长沙 410205)
根据2011年全国大学生数学建模竞赛A题,讨论了城市表层土壤重金属的污染问题。对于问题(1),采用Muller地积累指数法来描述土壤重金属污染程度;对于问题(2),利用因子分析法确定各元素的相关系数阵,分析出城市表层土壤重金属的污染主要来源;在问题(3)中,结合重金属污染传播特征及运用高次曲面的拟合建立城市表层土壤重金属污染源的数学模型。
Muller地积累指数法;因子分析法;函数拟合
1 问题的提出
随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,已成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、…、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。为此,将所考察的城区划分为间距1km左右的网格子区域,按照每平方公里1个采样点对表层土(深度0~10 cm)进行取样、编号,并用GPS记录采样点的位置。应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。另一方面,按照2km的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值(数据详见2011年全国大学生数学建模竞赛A题)。
现要求通过数学建模来完成以下任务:
(1)给出8种主要重金属元素在该城区的空间分布,分析该城区内不同区域重金属的污染程度。
(2)通过数据分析,说明重金属污染的主要原因。
(3)分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
2 问题的分析
对于问题(1),可利用 Matlab7.0、Mathematic7.0等数学软件将城市的地形图及8种重金属元素按浓度的高低分布图绘制出来,并借助Muller地积累指数法、单因子指数法、环境风险指数法等讨论污染程度。
对于问题(2),可利用因子分析法确定哪几种元素污染属同一原因,再对比8种重金属元素浓度分布图,并查找相关资料确定重金属污染的主要原因。
对于问题(3),可结合问题(2)中的重金属污染的主要原因来确定本区域的传播特点,拟定污染的主要地区并选择一至两种典型区域作为讨论对象,由附件中的数据进行高次曲面的拟合建立相关数学模型,通过对模型极值的讨论确定该地区的污染源位置。
3 模型假设
为了方便建模,做如下假设:城区的人口流动量是稳定的;各元素在土壤中的迁移速率是恒定不变且迁移方向为浓度高的地方指向浓度低的地方;各元素的质量不会有损失;如果某地区是工业废渣、生活垃圾的掩埋地或是处理场,不会对周围的环境造成重金属的污染;两种或几种重金属共同污染的地区,重金属的化合物之间发生的化学、生物及物理的反应忽略不记;由于大气流动带来的该城区外的污染忽略不记;由两个及以上的污染源造成污染的地区的交叉处与单一污染源造成的情况同样处理。
4 模型建立与求解
根据问题的分析及提供的数据,建立相关模型,利用Matlab、Mathematic等软件作图并求解模型。
4.1 问题(1)的解决
先根据数据,利用Mathematic7.0将该城区的地形图绘出(如图1所示,其中设正上方为正北,下同)。由图1不难看出,该城市的地形为东、北高西、南低,东部及北部为海拔不高的山区,中部也有一个小山丘。各功能区的区域界线不明显,说明生活区与工业区在一起。

图1 城市各功能区的地形图
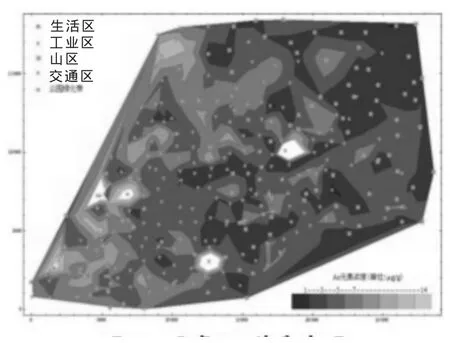
图2 元素As的分布图
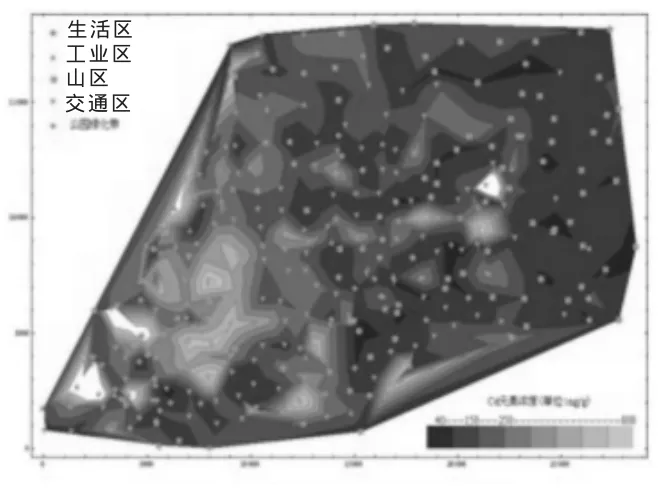
图3 元素Cd的分布图

图4 元素Cr的分布图
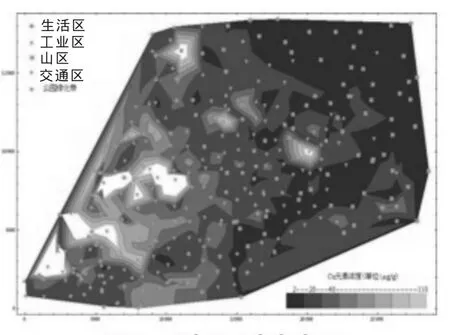
图5 元素Cu的分布图

图6 元素Hg的分布图

图7 元素Ni的分布图
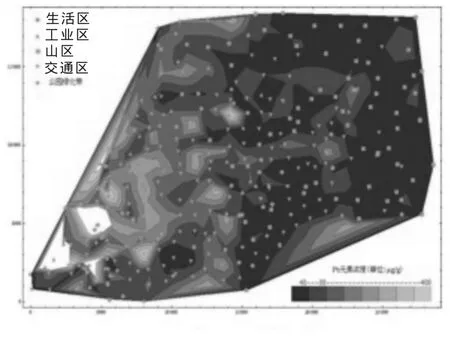
图8 元素Pb的分布图

图9 元素Zn的分布图
为了更快更准确地找出各种重金属元素的空间分布,根据数据利用Mathematic7.0绘制其空间分布图(如图2~图9)。
由图2可知元素As主要分布在中部及西南部,集中在工业区和交通区这两个区域;类似可知元素Cd主要分布在靠近东部的山区及西部城区边界地段,主要集中在生活区、工业区及交通区;元素Cr主要分布在西南地区,东部山区也存在一浓度较高的地方,主要集中在生活区、交通区及工业区的周边地区;元素Cu主要分布在西南大部及西北部地区,浓度较高的区域集中在工业区及其周边、交通区;元素Hg是工业区域污染最严重的重金属元素,从中部开始,往西的所有地区都受到了污染,特别是西南地区污染程度极其严重;元素Ni是这8种重金属元素中污染最轻的,只是集中在西南部方圆4km2的区域内;元素Pb也主要集中在西南地区的工业区周边;元素Zn的污染区域仅次于Hg,主要集中在中西部,西南部工业区及其周边、交通区尤为严重。
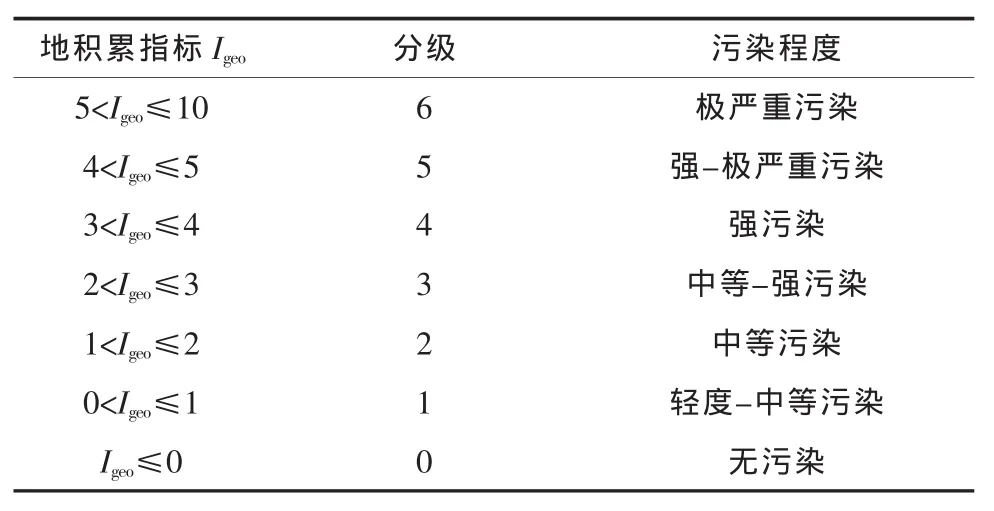
表1 Muller地积累指数分级
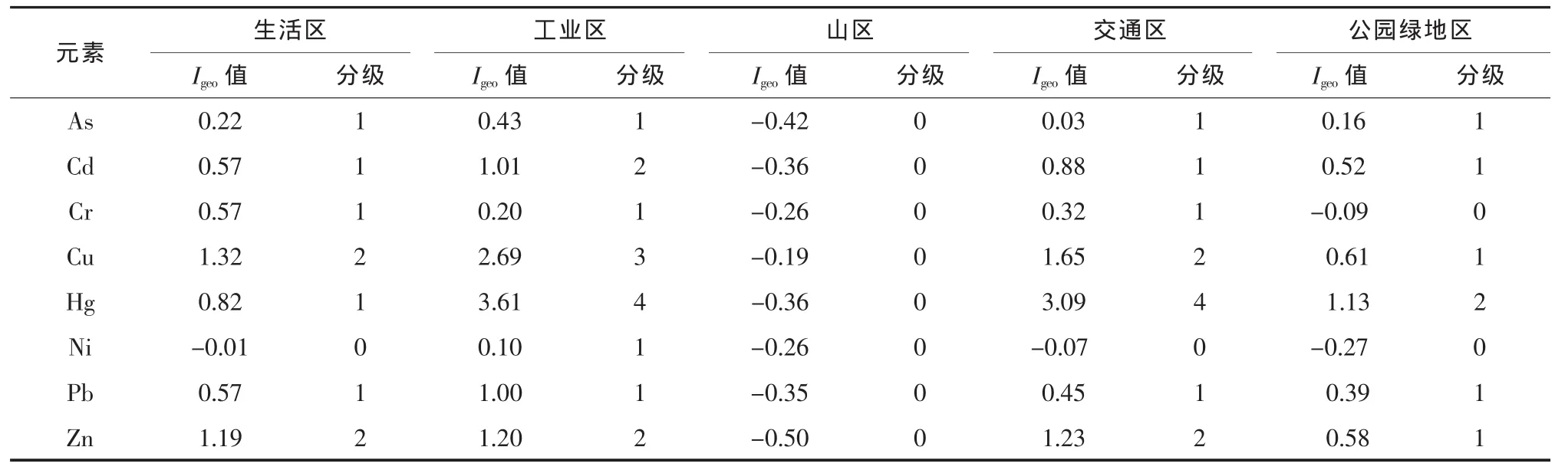
表2 8种重金属元属按背景值计算地积累指数和分级
Muller[2]曾提出用地积累指数定量评价沉积物中的重金属污染程度,并规定了相应的污染程度级别划分标准(表1),这种评价方法也可用来评价土壤中重金属的污染程度及其分级情况[3]。
根据数据,按公式 Igeo=log2[Ci/(1.5Bi)]计算,此城市各功能区土壤中8种重金属元素的Muller地积累指数及分级情况见表2。从表中可以得出:
从横向上来比较,工业区的总体污染程度最高,其次污染的程度从重到轻分别是交通区>生活区>公园绿化区>山区,这与经采样分析所得的数据是一致的。从纵向上来看,生活区中Ni元素没有造成污染,而 As、Cd、Cr、Hg、Pb 这五种元素都达到轻度-中等污染,而Cu和Zn达到了中等污染。工业区中,As、Cr、Ni、Pb 四种元素达到了轻度-中等污染,Cd、Zn达到了中等污染,Cu达到了中等-强污染,Hg元素造成了强污染。山区中,8种元素都没有造成污染。交通区中,Ni元素没有造成污染,As、Cd、Cr、Pb等四种元素造成了轻度-中等污染,Cu、Zn元素达到了中等污染,Hg元素造成了强污染。公园绿化区中,Cr、Ni元素没有造成污染,As、Cd、Cu、Pb、Zn 五种元素造成了轻度-中等污染,Hg元素造成了中等污染。
4.2 问题(2)的解决
此问题要求通过数据分析,说明重金属污染的主要原因。
现以生活区为例来具体说明重金属污染的主要原因,其他区域可类似讨论。
首先对附件2中的数据做一定的处理,分别求出各种元素的测定平均值、测定最大值、测定最小值、方差、标准差(见表3),然后与其在该地区的背景值进行比较;再由因子分析法将8种元素的浓度相关系数阵求出(见表4);最后根据这些数据特征进行分析。
从表3可以看出,8种元素的均值除Ni以外,其余都大于背景值,说明生活区的其他7种元素均造成了不同程度的污染,而且Cu和Zn两种元素的实测平均值是背景值的3倍多,说明这两种元素对生活区造成的污染最为严重。
如果某两种重金属的含量有显著的相关性(相关系数比较大),说明它们有相同来源的可能性较大,否则来源可能不止一个。从表4中可以得出Cd、Cu、Pb重金属两两相关,且相关性比较大,说明这几种元素来自同一种污染源的概率较大。其中Pb与Cd的相关系数最大,达到了0.801 82,表明这两磨损以及煤燃烧产生的粉尘、烟尘中均含有锌及化合物。山区的Cr、Ni元素的相关系数较大,说明这里有富含Cr和Ni的矿藏。观察交通区的分布图知道其与工业区、生活区紧密相连,可以猜想,运输工业废料及生活垃圾时产生的扬尘也是该区域遭到污染的主要原因之一。本城市的大部分公园绿化区与工业区和生活区相邻,由此可见该区受工业区的影响相当大,极有可能是工业废水(气)排放不当、生活垃圾的随意堆放造成的污染,当然公园绿化区的落叶、凋落花果的腐烂也有一定的影响。种元素所造成的污染及有可能是同一原因造成的,其次是Ni和Cr,它们的相关系数为0.527 05,说明也有一定的联系。
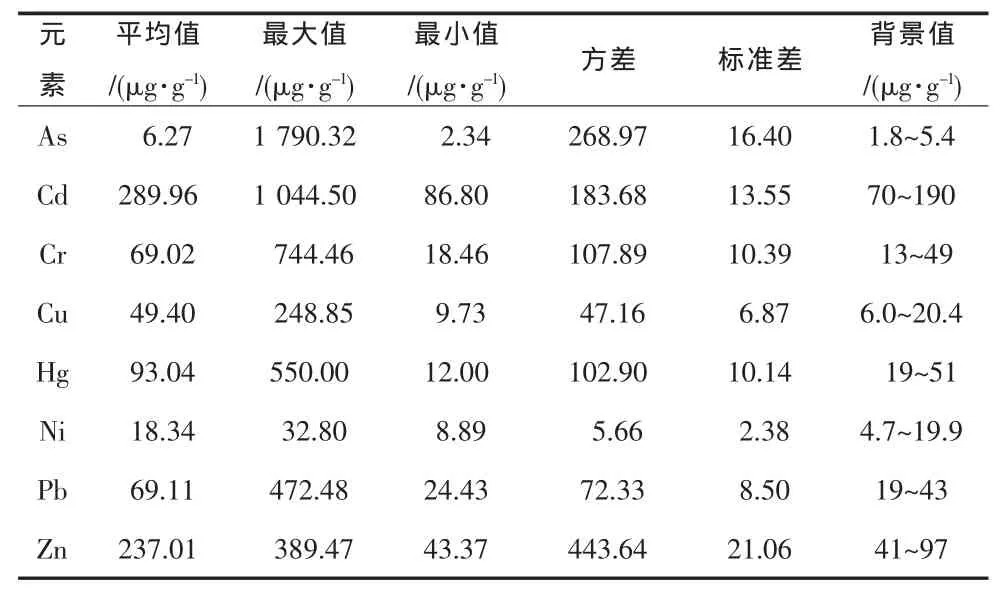
表3 生活区8种重金属测定结果
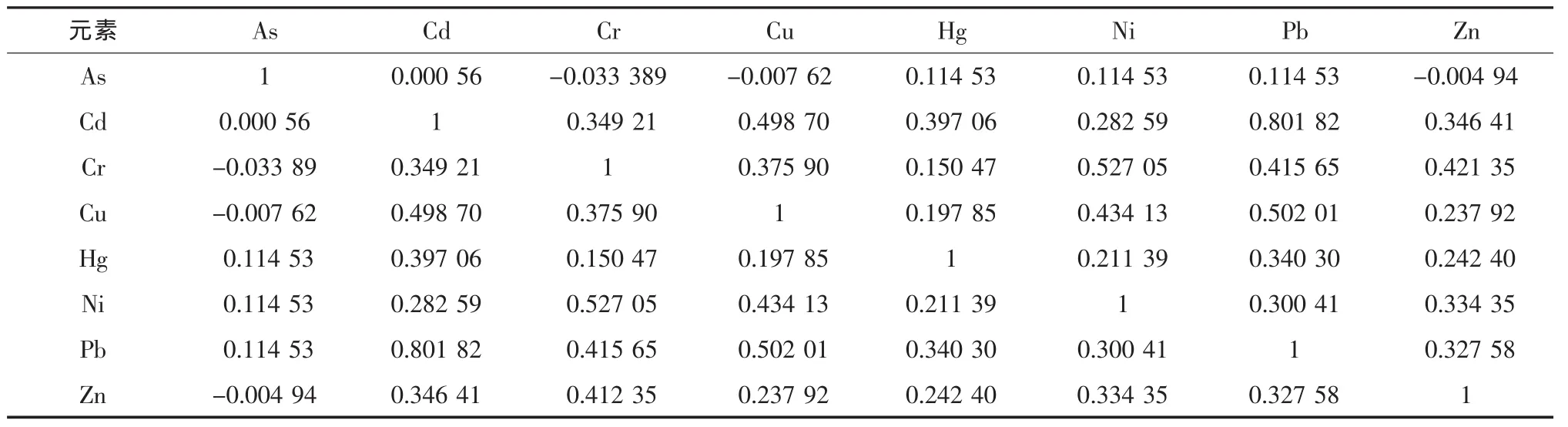
表4 生活区8种重金属元素的相关系数阵
生活区是人口密集区,我们认为,人类所带来的生活垃圾、煤燃烧产生的粉尘、烟尘、房屋的拆迁过程中许多毁损的家具设施以及建筑垃圾等对周边环境会造成一定的污染。另外,生活区的交通流量非常大,交通工具中尾气排放、行驶中所击起的尘埃及汽车轮胎磨损产生大量的有害气体,其中含有Pb,Zn,Cu 等多种重金属元素[3],这些重金属元素随扬尘进入周围的土壤,也造成了生活区土壤重金属污染。
结合化学知识,这几种元素的污染主要来自镍铬合金、电池、陶瓷原料、汽车轮胎磨损、汽车尾气的排放以及煤燃烧产生的粉尘、烟尘,也有可能是来自周边工厂的工业废水。
采用同样的方法分析其他四个区的污染原因。工业区的污染程度相当高,结合化学知识分析出工业区重金属污染的主要原因是铜锌矿的开采和冶炼,电镀、染料、电池和化学工业等排放的废水和废气,金属加工、机械制造、钢铁生产、塑料、电池、电子等工业排放的废水;汽车排出的含铅废气、汽车轮胎
综上所述,城市表层土壤重金属的污染主要来源于工业污染,其次是交通污染和生活垃圾污染。工业污染大多通过废渣、废水、废气排入环境,在人和动物、植物中富集,从而对环境和人的健康造成很大的危害;交通污染主要是汽车尾气的排放;生活污染主要是一些生活垃圾的污染,如废旧电池、破碎的照明灯、没有用完的化妆品、上彩釉的碗碟等。目前我国塑料生产企业的工艺、设备、技术研发较落后,是造成污染严重的主要原因,而管理不善、地方保护及人们环保意识淡薄,也加剧了污染。
4.3 问题(3)的解决
本节主要分析重金属污染物的传播特征,并由此建立模型,来确定污染源的位置。
表5中,x表示采样点的横坐标;y表示采样点的纵坐标;z表示采样点的海拔高度;Ci表示元素i的浓度,单位是μg/g或ng/g;Igeo表示地累积指数;Bi表示元素i的背景值,单位是μg/g或ng/g;其中i代表 As,Cd,Cr,Cu,Hg,Ni,Pb,Zn。
重金属是指密度在4.0g/cm3以上约60种元素或密度在5.0g/cm3以上的45种元素。砷、硒是非金属,但是它的毒性及某些性质与重金属相似,所以将砷、硒列入重金属污染物范围内。随着全球经济化的迅速发展,含重金属的污染物通过各种途径进入土壤,造成土壤严重污染。比如:大多数重金属通过自然沉降和雨淋沉降进入土壤圈,使用含有Pb、Cd、Hg、As等的农药和不合理地施用化肥都可以导致土壤中重金属的污染,废弃物堆中重金属含量一般比较高,污染的范围一般以废弃物堆为中心向四周扩散。重金属元素正是以上述主要途径进行传播,可以得出它的传播特征必以某处为中心,随着附着物向四周流散开来,但不会向很远的地域扩散,此外重金属元素含量会随着土壤深度的增加而呈现降低的趋势。
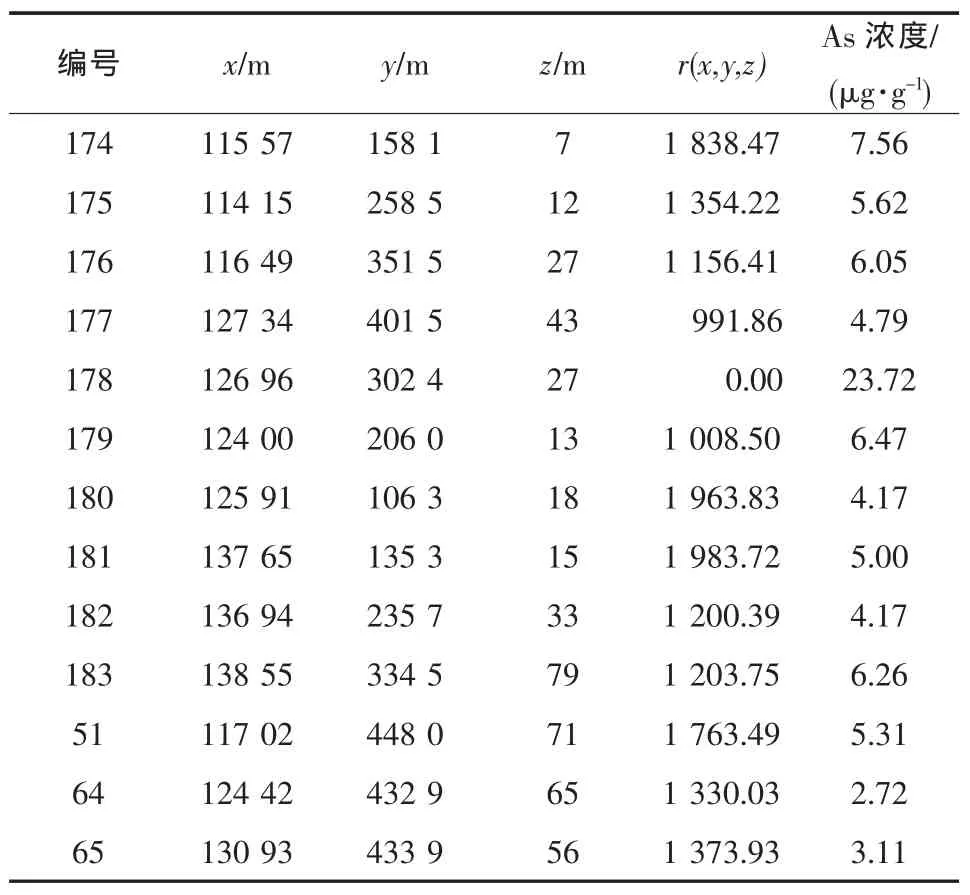
表5 178点附近检测点的数据
4.3.1 建立一维模型
首先由319个数据点通过Mathematica软件作图,得到1个近似的地形图和8个近似的重金属浓度分布图(图1~图9)。浓度分布图中颜色越浅的地方浓度越高,尤其是在白色区域内一般都有几个浓度非常高的检测点,而周围区域的检测点重金属浓度相对要低很多,如图10中的178、84所处的位置。据此我们以白色区域内的检测点为球心O,根据三维坐标计算出附近检测点到球心O的距离r,画出r与浓度C的函数关系图,用Excel拟合出多项式曲线,并计算相关系数。
从表5及图10可以看到178号点具有最高的As浓度,所以以178号点为球心,计算出附近各点所处的半径值,以半径为x轴,As浓度为y轴作图(如图11所示)。图11给出了该拟合曲线,相关系数 R 的平方值为0.950 2, 方程为:C=-10-11r4+5×10-8r3-6×10-5r2+4.7×10-3r+23.7,该函数有 3 个极值点,41.27,1 473.98,1 609.76,认为极大值对应污染源,除了r=41.27m处有一大型污染源外,r=1 609.76m处也应该存在一小型污染源。
其他元素的相关模型可类似讨论。
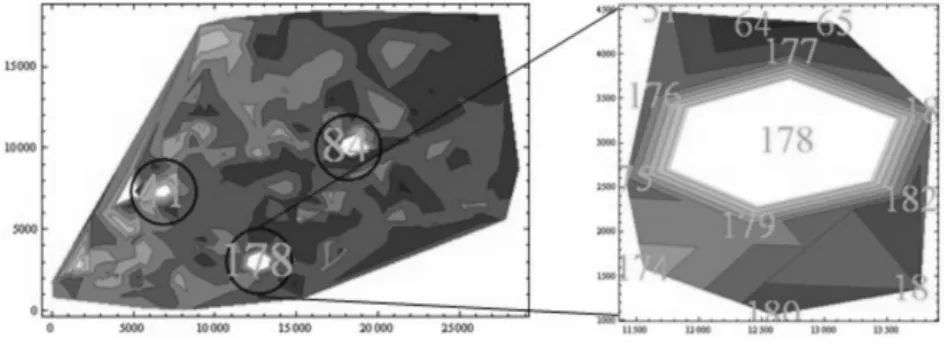
图10 元素As以178号点为圆心取点

图11 以178号点为球心拟合四次方曲线

图12 以178号点为球心拟合五次、六次方曲线
4.3.2 建立多维模型
根据重金属元素的传播特征,且由于不同的地方各种元素的浓度各有差异,不妨设各元素的浓度函数为:
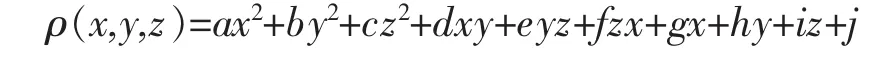
其中 x,y,z 为各点的坐标值,a,b,c,d,e,f,g,h,i,j为选定系数。
以元素As为例,选择浓度比较集中且较高的区域(3 000≤x≤8 000;4 500≤y≤9 000)的 10 个点代入上式,由Mathematic算得
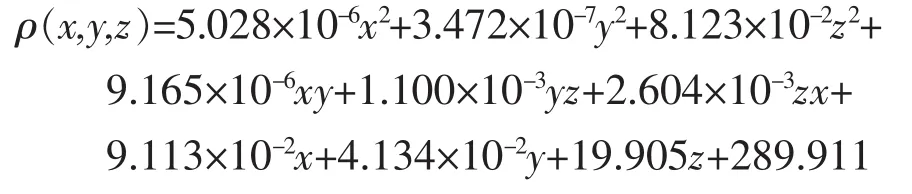
为所求浓度函数 ρ(x,y,z)的极值点,故令∂ρ/∂x=0,∂ρ/∂y=0,∂ρ/∂z=0。利用 Mathematic 解得(x,y,z)=(5 258.08,7 244.48,10.806),将所求得的 x、y、z的极值代回到方程中,算得浓度ρmax=2 033.56,说明此点并非污染源。
其余元素的其他区域也可进行类似求解。
4.4 模型的评价
(1)模型的优点
关于一维模型的优点,主要是容易操作,且可直接通过Excel计算并作图,且由于函数是关于半径r的四阶多项式,故图形直观简单;其次是该种拟合方式精度高,与实际情况接近,所求极值即为污染源;多维模型的优点之一是思路清晰明了,且由于采取的是局部分析法,精确度也比较高。
(2)模型的不足
一维模型与多维模型均是采取的局部分析的方法,即讨论的对象不是整个城区,而是通过搜索找出某浓度很高的区域,故点的选取对模型的好坏影响较大;再有求出的极值有可能是极小值点。
为了更准确的拟合浓度函数,可以用更高次的坐标函数来拟合,3维函数的2次项有10项,3次项有15项,m次项有项,点数越多,拟合出来的函数应该与实际函数越接近。
为了更好地研究城市地质环境的演变模式,还应收集该地区的每年生活、工业等重要污染源的垃圾排放量,以及每年的生物降解量,降雨量对重金属元素扩散的影响,空气污染也应该考虑进去,综合多方面的因素就可以确定传染源的位置。
[1]全国大学生数学建模组委会.2011全国大学生数学建模竞赛A题[E].http://www.shumo.com.
[2]Muller G.Index of Geoaccumulation in Sediments of the Rhine River[J].Geojournal,1969,2(3):108.
[3]张明亮,王海霞.煤矿区矸石山周边土壤重金属污染特征与规律[J].水土保持学报,2007,21(4):
[4]刘延良,高松武次郎,左濑裕之.日本城市土壤的重金属污染研究[J].环境科学研究,1996,9(2):47-51.
[5]菲尔汗·汉杰尔,潘丽英,陈勇,等.汽车废气中的铅对城市土壤污染状况调查[J].干旱环境检测,2002,46(3):154-161.
[6]王雄军,赖健清.基于因子分析法研究太原市土壤重金属污染的主要来源[J].生态环境,2008,17(2):671-676.
Analysis and Evaluation of Heavy Metal Pollution on Urban Topsoil
CHENG XiayanZHANG Yun
(Hunan First Normal University,Changsha 410205)
Combined with the programming A of CUMCM 2011,this paper analyzes and evaluates the heavy metal pollution on urban topsoil.For problem one,we describe the degree of soil heavy metal pollution by Muller Accumulation Index Method.For the second problem,Factor Analysis Method is used to determine the elements of the correlation coefficient matrix.We analyze which is the sources of pollution of urban topsoil heavy metal pollution.In the third problem,combined with the propagation characteristics of heavy metal pollution,we use the High-order Surface Fitting to establish the mathematical model of heavy metal pollution on urban topsoil.
Muller accumulation index method;factor analysis method;functions fitting
X825
A
1673-1980(2012)05-0112-06
2012-04-11
湖南省教育科学“十二五”规划课题(XJK011BGD031);湖南省高校青年基金项目(11B029);湖南第一师范学院院级项目(XYS11Z20)
成夏炎(1984-),男,湖南湘潭人,硕士,助教,研究方向为组合与优化。

