永磁同步电机磁场谐波抑制的补偿控制仿真

吴志红，李根生，朱 元

（1.同济大学 汽车学院，上海 201804；2.同济大学 中德学院，上海 200092）

永磁同步电机具有高效率、高能量密度、启动转矩大等特点，随着钕铁硼永磁材料的性能日益提高以及矢量控制理论、高性能处理器和大功率高开关速度功率电子元器件的发展，永磁同步电机的应用领域不断扩大［1］.

根据转子的结构，永磁同步电机可分为面贴式和内置式两种.对于面贴式结构，可以通过改变永磁体的形状和极弧宽度，或者采用其他有效措施，使永磁体励磁磁场尽量接近正弦分布.对于内置式结构，由于永磁体嵌入转子结构内，提高了机械性能，使电机更加坚固可靠，可在高速下运行；同时该结构决定了电动机的直轴同步电感小于交轴同步电感，由于交直轴电感的不等，提供了额外的磁阻转矩，扩大了弱磁范围.内置式永磁同步电机的这些特性，非常适合电动汽车的要求，成为电动汽车的首要选择.

但是对于内置式永磁同步电机，在转子永磁体励磁磁场中含有谐波分量，这将增加定子绕组内磁链的谐波分量，增大电机的损耗，使电机运行的温度升高［2－3］.特别是在高速运行时，因为弱磁控制会使得磁链基值减小，但谐波部分仍保持不变，因此谐波铁损所占比例将增大，且会变得更为明显，同时导致输出的电磁转矩具有周期性的波动，将增加电机的振动和噪音［4－7］，这时对谐波的抑制尤为重要.国内外一些学者从电机设计方面对永磁体磁场进行研究，利用有限元等方法来分析永磁体磁场，并提出了一些相关改进方法来削弱谐波分量［8－13］.但仅从电机设计方面很难使励磁磁场呈正弦分布，并且会增加制造成本，因此除了从电机设计方面，还应该从控制的角度采取措施消除或减少永磁体励磁磁场的谐波分量带来的影响［1］.

笔者对电机转子磁场谐波进行测量，根据测量结果建立含有谐波的电机模型，然后对该模型进行谐波补偿控制.对仿真结果进行频谱分析，结果表明在谐波补偿控制下，磁链谐波得到有效的抑制.

1 磁场谐波测量及电机模型

在实际的永磁同步电机中，特别是对内置式结构，永磁体励磁磁场很难做到正弦状，而含有（2n－1）次谐波［1，5］，因此永磁体励磁磁场B（θ）可以表示为一系列谐波分量的和，其中θ为转子位置电角度，谐波的幅值随着次数的增高而迅速衰减.

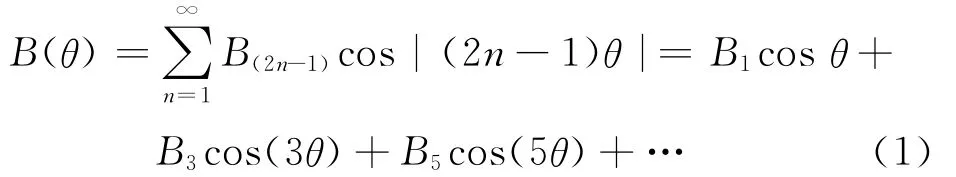
为了测定永磁体磁场在定子绕组中产生的磁链Ψf中的谐波分量，首先在试验台上进行空载试验，让电机三相开路，然后把电机拖转到某一恒定的转速，测量三相之间的线电压uAB和uAC，通过计算后可得到单相的相电压.实验选用电机参数如表1，实验结果如图1和图2所示，图1为ABC三相中A相的空载反电动势uA，图2为空载反电动势uA的快速傅里叶变换（fast Fourier transform，FFT）分析结果.

表1 电机参数Tab.1 Motor parameters

对实验结果分析可以得到各次谐波幅值在反电动势基波幅值中的系数，其中5次谐波占基波的2.3%，7次谐波占1.1%.当电机三相为Y连接，且没有中线时，反电动势中将不再含有3次和3次倍数次谐波，这时5次和7次谐波的影响是最主要的.

图2 A相空载反电动势谐波分量Fig.2 Harmonic components in no－load of phase A

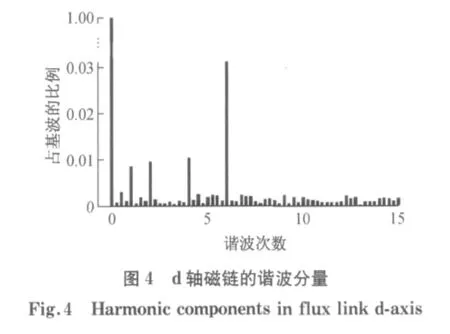
从ABC轴到旋转dq轴的转换关系由公式（2）给出，根据实验得到的三相相电压和转子位置，通过公式（2）转换到dq轴，式中ud，uq为dq轴电压，uA，uB，uC为 A，B，C轴电压.ABC轴电压中的5次和7次谐波将在旋转dq轴电压中产生6次和12次谐波，在只考虑6次谐波的影响下，有空载反电动势e0＝ωeΨf0，ωe为电角速度.根据测得的e0和转速信息可得到转子永磁体磁场在dq轴产生的磁链，该磁链中含有与定子绕组中产生的反电动势同样次数的谐波分量.一个机械周期转子永磁体磁场在dq轴产生磁链的变化如图3所示.其中横坐标为机械角度，因为每个电周期有6次波动，实验采用的电机为4对极，所以每个机械周期内有24次波动.通过对磁链的FFT分析，可以得到dq轴的6次谐波分量Ψd6和Ψq6.图4给出了d轴谐波分量的FFT分析.

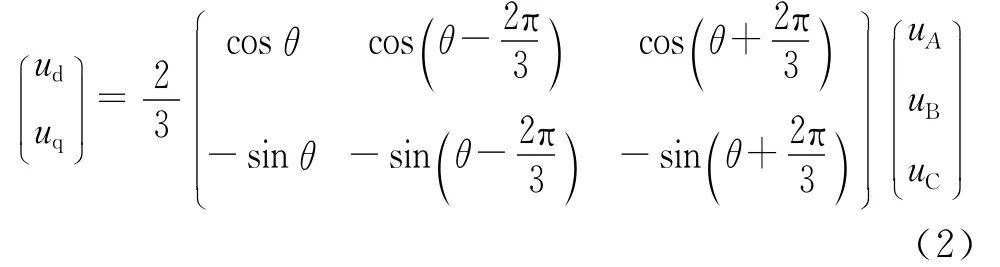
永磁同步电机在dq坐标系下的数学模型为

式中：id，iq为dq轴电流，p为微分符号.

永磁体磁场在dq轴的分量实际由基值和谐波组成，其中谐波是θ的函数，可得到dq轴磁链Ψd和Ψq为

由以上两式可以看出dq轴磁链只是在原来的磁链基础上多出了6次谐波项，因此对于电压方程来说也只需要在原来的电压基础上加上自感产生的电压和另外一个轴互感产生的电压，可得dq坐标系下的电机模型为

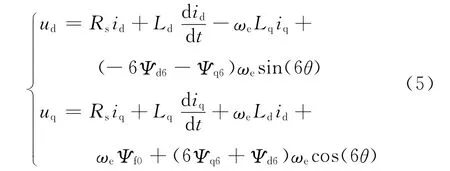
含有6次谐波的电机电磁转矩方程为

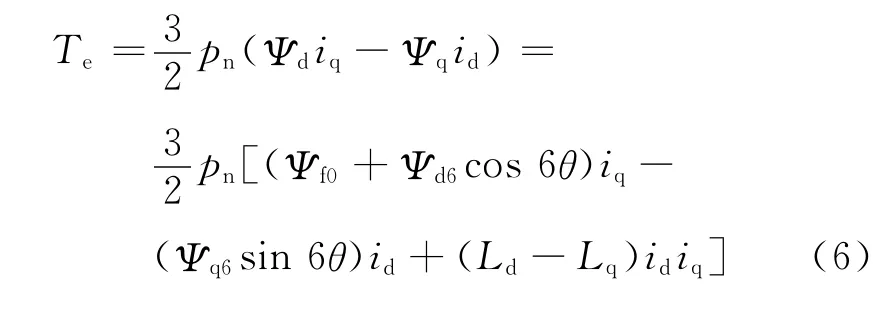
2 铁损分析

在永磁同步电机中，由于转子与定子磁场同步旋转，所以转子的涡流损耗一般很小，与定子涡流损耗相比可以忽略，定子铁损包括磁滞损耗和涡流损耗［3，14］.

2.1 磁滞损耗

在交流磁路的铁心被反复磁化和去磁时，磁通变化滞后于励磁电流变化，使磁通密度与磁场强度之间呈滞回线关系，每次循环，单位体积铁心中的磁滞损耗等于磁滞回线面积，这部分损耗可由经验公式得到：

基波磁滞损耗Ph1

n次谐波磁滞损耗Phn

总磁滞损耗Ph

式中：f为磁场变化频率；Bm为基波磁场强度；Kh和n是由材料确定的常数.

2.2 涡流损耗

在电机中，为了产生强磁场，都将定子绕组缠绕在铁心上，这样线圈内电流变化时，铁心就相当于处于变化的磁场中，内部产生的电压将在铁心内部产生涡流.涡流导致能量损失和温度升高，涡流损耗的经验计算公式如下：

基波磁滞损耗Pe1

n次谐波磁滞损耗Pen

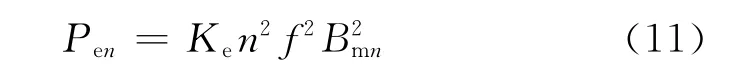
总磁滞损耗Pe

式中：Ke是由定子铁心材料和定子硅钢片厚度确定的常数.

总的铁损Pi

在电机运行中，定子铁损主要由主磁链和低次谐波引起，其中主磁链用来产生电机所需的电磁转矩，低次谐波将产生额外的损耗，并引起电磁转矩的波动，因此高效率的电机控制需要对谐波部分进行补偿，以减少铁损提高效率.

3 磁链和转矩补偿仿真结果

在永磁同步电机的矢量控制中，永磁体在交轴产生的磁链接近于零，定子中的涡流损耗和磁滞损耗主要由直轴磁链产生.磁链补偿控制器目标是通过控制dq轴电流使直轴磁链的谐波分量降低以达到减少涡流损耗和转矩波动.其中补偿量要根据磁链6次谐波幅值和当前的机械角度θm来计算，转子不同位置对应的磁链不一样，所以补偿需按照相位来进行.为了避免由PI控制器带来的相位滞后及频宽的限制等影响，本文的补偿方法是将补偿量直接加在dq轴的电压命令上.图5为提出的控制结构，图中和分别为dq轴的电流命令值.在进行补偿控制时，控制器根据当前的机械角度θm计算或查表得到补偿量Cd，然后对dq轴进行谐波补偿.

图5 磁链补偿控制结构Fig.5 Control structure of flux compensation

图5中Cd补偿d轴磁链，目的是减小谐波分量，由公式（14）可得补偿控制量，式中 Ψd6（θm）是根据机械角度得到d轴对应相位的磁链6次谐波幅值，KΨ的选取与d轴电流控制环的增益有关.

图5中Cq是对电磁转矩进行补偿，以减小电磁转矩波动，由公式（15）可得补偿控制量，其中Ψq6（θm）是根据机械角度得到q轴对应相位的磁链6次谐波幅值，KT的选取与q轴电流控制环的增益有关.

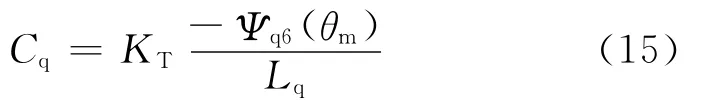
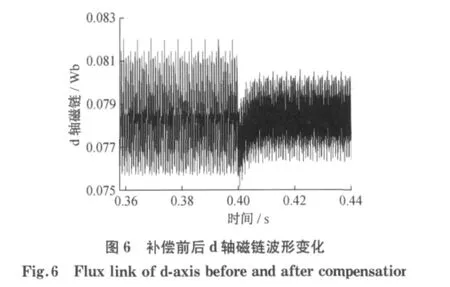
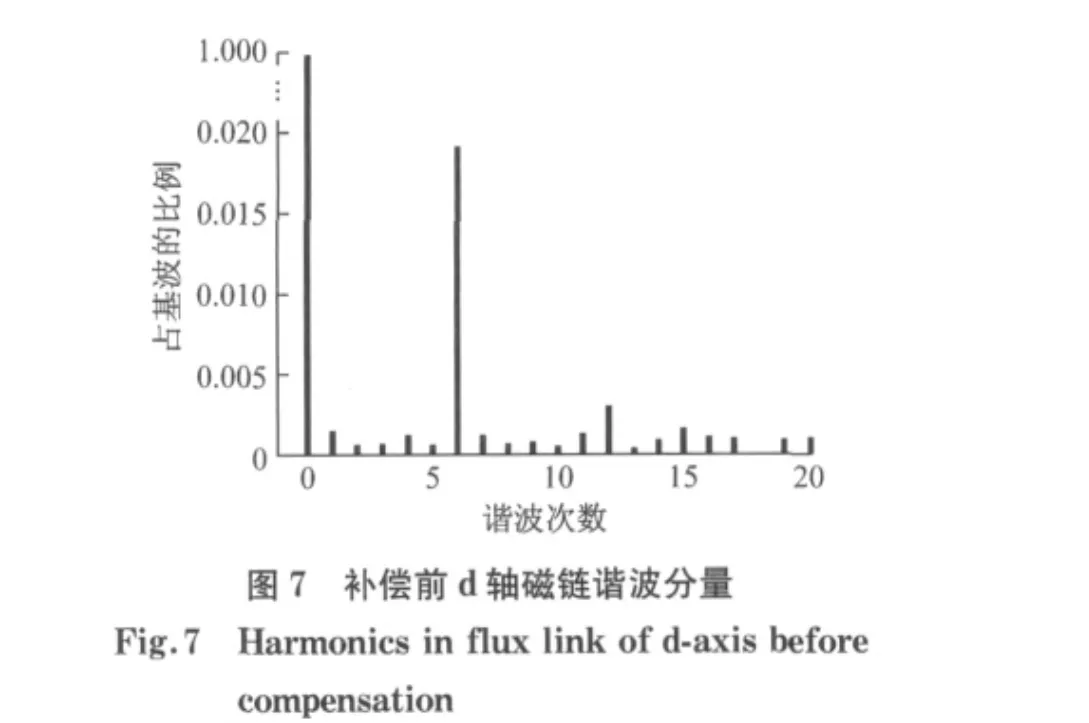
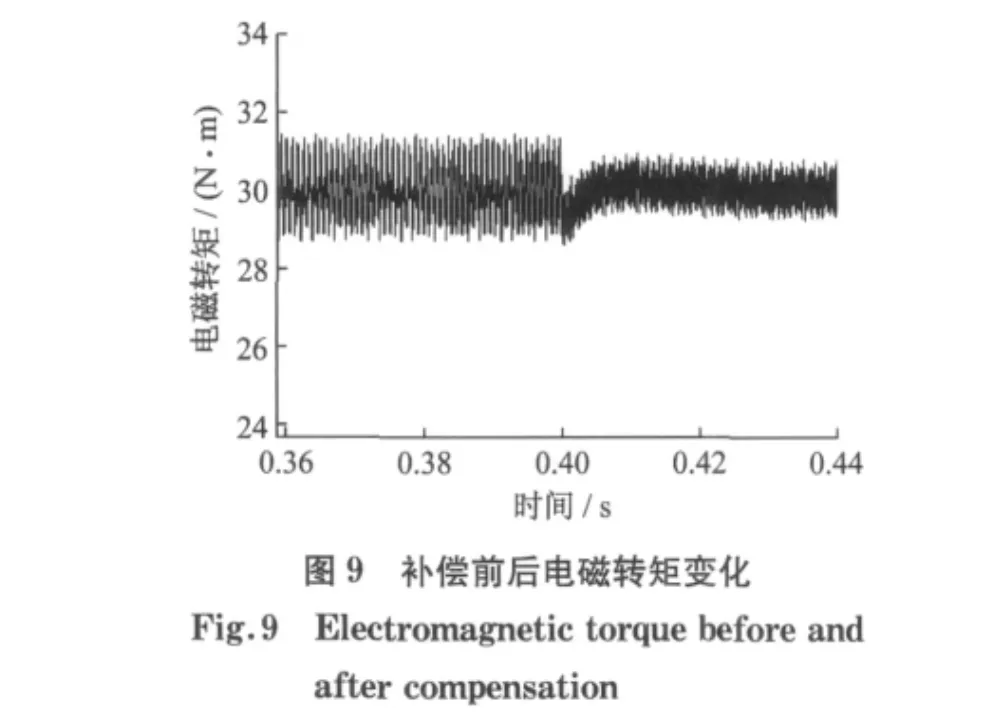
按照图5的控制结构在Matlab／Simulink中建立电机控制系统的仿真模型，仿真电机参数如表1所示，仿真结果是在电机机械角速度为600 rad·s－1，负载T＝30N·m的条件下进行.在到达稳态时保持命令值不变，在时间t＝0.4s时刻开始进行补偿，图6～8为d轴磁链及FFT分析结果，图9～11为电磁转矩及FFT分析结果.

图6为d轴磁链在补偿前后的变化，可以看出在t＝0.4s时刻开始补偿后，d轴磁链的波动明显减小.同时从FFT分析结果（见图7和图8）可以看出，6次谐波部分从补偿前的2%降到0.6%.转子磁链谐波分量的降低，会减少定子的铁损，提高电机运行效率.

图9为电磁转矩补偿前后的仿真结果，从t＝0.4s开始补偿后电磁转矩波动明显减小，对电磁转矩进行FFT分析结果如图10和图11所示，可以看出，6次谐波部分从补偿前的2.5%降到0.5%左右.电磁转矩波动减小，将会减少电机的振动，降低噪音.

4 结论

为了提高对永磁同步电机的控制性能，在转子同步旋转坐标系下对永磁同步电机的磁链进行了补偿.分析和仿真表明，补偿后减少了磁链中的谐波部分，降低了定子的铁损，同时通过对电磁转矩的补偿，减小了转矩波动.

［1］王成元，夏加宽，杨俊友，等.电机现代控制技术［M］.北京：机械工业出版社，2006.WANG Chengyuan，XIA Jiakuan，YANG Junyou，et al.Modern motor control technology ［M］. Beijing：China Machine Press，2006.

［2］徐永向，胡建辉，胡任之，等.永磁同步电机转子涡流损耗计算的实验验证方法［J］.电工技术学报，2007，22（7）：150.XU Yongxiang， HU Jianhui， HU Renzhi， et al. An experimental verification method of calculation for rotor eddy current losses in PMSMs ［J］. Transactions of China Electrotechnical Society，2007，22（7）：150.

［3］胡笳，罗应立，李志强，等.永磁电动机不同运行条件下的损耗研究［J］电机与控制学报，2009，13（1）：11.HU Jia，LUO Yingli，LI Zhiqiang，et al.Investigation of losses in permanent magnet synchronous motor under different operation conditions［J］.Electric Machines and Control，2009，13（1）：11.

［4］Wallmark O.Control of a permanent magnet synchronous motor with non－sinusoidal flux density distribution ［D］.Göteburg：Chalmers University of Technology，2001.

［5］李景灿，廖勇.考虑饱和及转子磁场谐波的永磁同步电机模型［J］.中国电机工程学报，2011，31（3）：60.LI Jingcan， LIAO Yong. Model of permanent magnet synchronous motor considering saturation and rotor flux harmonics［J］.Proceedings of the CSEE，2011，31（3）：60.

［6］Yamazaki K，Ishigami H.Rotor－shape optimization of interiorpermanent－magnet motors to reduce harmonic iron losses［J］.IEEE Transactions on Industrial Electronics，2010，57（1）：61.

［7］Životic－Kukolj V，Soong W L，Ertugrul N.Iron loss reduction in an interior PM automotive alternator［J］.IEEE Transactions on Industry Applications，2006，42（6）：1478.

［8］Tseng K J，Wee S B.Analysis of flux distribution and core losses in interior permanent magnet motor［J］.IEEE Transactions on Energy Conversion，1999，14（4）：969.

［9］Schifer R，Lipo T A.Core loss in buried magnet permanent magnet synchronous motors［J］.IEEE Transactions on Energy Conversion，1989，4（2）：279.

［10］Han S－H，Jahns T M，Zhu Z Q.Analysis of rotor core eddycurrent losses in interior permanent－magnet synchronous machines［J］.IEEE Transactions on Industry Applications，2010，46（1）：196.

［11］Xiao X，Chen C M.Reduction of torque ripple due to demagnetization in PMSM using current compensation ［J］.IEEE Transactions on Applied Superconductivity，2010，20（3）：1068.

［12］Lee G－H，Kim S－I，Hong J－P，et al.Torque ripple reduction of interior permanent magnet synchronous motor using harmonic injected current［J］.IEEE Transactions on Magnetics，2008，44（6）：1582.

［13］Thomas S－H，Jahns T M，Soong W L.Torque ripple reduction in interior permanent magnet synchronous machines using the principle of mutual harmonics exclusion［C］∥IEEE Industry Applications Conference，2007.42nd IAS Annual Meeting.New Orleans.IEEE，2007：558－565.

［14］Gupta B R，Singhal V.Energy conversion［M］.New Delhi：New Age International（P）Ltd，2007.