点扩散函数高斯拟合估计与遥感图像恢复
杨利红,赵变红,张星祥,任建岳*
(1.中国科学院 长春光学精密机械与物理研究所,吉林 长春130033;2.中国科学院 研究生院,北京100039)
1 引 言
图像恢复的目的是从被退化函数模糊和被噪声污染的图像中尽可能地恢复出真实的场景。经典的图像恢复方法有维纳滤波、约束最小二乘法滤波、Lucy-Richardson 算法等,这些方法均需要知道退化函数的类型和参数才能取得一定的恢复效果[1-3]。由于航天遥感相机运行的空间环境特殊,图像获取的大气条件多变,因此,往往无法获得准确的退化函数,只能利用成像系统的参数或获取的图像对系统退化函数进行辨识,然后,根据估计出的退化函数,选择合适的算法对图像进行恢复。
随着航天科技的发展,遥感图像恢复取得了很多成果,退化函数估计是其中的一个重要研究方向。航天遥感相机成像过程中的退化函数为点扩散函数( PSF) ,PSF 傅里叶变换的归一化模值为调制传递函数( MTF) 。顾行发等人提出了模拟理想靶标检测卫星在轨MTF,根据45°方向的MTF 数据建立插值二维MTF 矩阵来对图像进行恢复[4],此方法需要人工铺设模拟点光源的靶标,适用性不强;陈强等人利用实验室测定的相机系统MTF 值来近似遥感图像的MTF 值,利用指数调节MTF 曲线来进行图像恢复[5],忽略了卫星实际运行环境和成像条件对MTF 的影响;张朋等人利用系统模型法估计MTF,此种方法没有考虑大气的影响,适用于获取的图像没有特征地物的情况。上述方法通过估算MTF 在频域内对遥感图像进行恢复,需要将MTF 对应的成像系统的空间频率转换为傅里叶频率,目前还没有定论,使用受到一定的限制。
本文直接利用图像中的特征地物估计成像系统的PSF,通过高斯拟合对PSF 进行调整,使之更符合实际成像系统的情况。以拟合后的PSF 作为参数,使用自适应维纳滤波进行图像恢复。在图像恢复前,先进行去噪预处理,去除遥感图像上的周期条带噪声,增强图像恢复的效果。
2 图像退化与恢复
2.1 图像退化模型
图像的退化过程可以被模型化为一个退化函数和一个加性噪声项。原始地物的图像经过成像系统和大气发生了退化,在图像的获取和传输过程中又引入了大量噪声,从而使最终获得的图像是降质的图像,存在着不同程度的模糊。
若退化函数是线性空间不变的,则图像退化过程在空间域可表示为原图像f(x,y) 和退化函数h(x,y) 的卷积并叠加噪声n(x,y) ,形成退化图像g(x,y) ,具体形式为:

由卷积定理可知,空间域两个函数的卷积在频率域中表示为它们傅里叶变换的乘积,因此,退化过程可在频域表示为:

式中:F(u,v) ,H(u,v) ,N(u,v) ,G(u,v) 分别为f(x,y) ,h(x,y) ,n(x,y) ,g(x,y) 的二维傅里叶变换。
2.2 图像恢复理论
图像恢复用于减轻或消除图像获取过程中发生的退化。如果知道退化函数和噪声的相关知识,即可以采用与退化相反的过程恢复退化图像,包括去噪和去卷积两个过程。在频率域中可表示为:
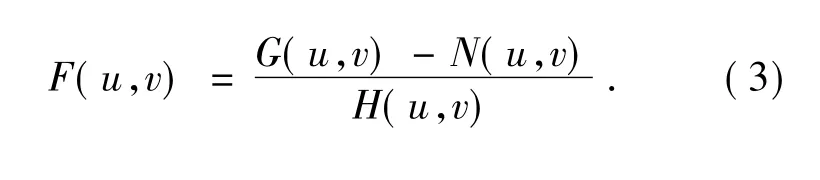
噪声是一个随机分量,很难确切估计,图像恢复会放大图像中的噪声,因此,图像恢复要去除噪声,消除噪声对它的副作用。去噪既可以在空间域也可以在频率域中进行。常用的方法是根据噪声的特点,选择合适的滤波器滤除噪声。卷积运算在频率域可转换为乘法运算,其逆运算在频域中为除法运算,因此,去卷积通常在频域中进行。最后,对得到的结果F(u,v) 进行傅里叶反变换即可得到恢复图像。
3 遥感图像恢复
3.1 去噪预处理
图像恢复主要是提升图像的高频部分,增强图像的边缘细节,而噪声在图像中也表现为高频成分,恢复图像的同时会使噪声增大。因此,在图像恢复之前进行去噪处理,可以避免噪声放大淹没图像细节。时间延迟积分( TDI) CCD 相机图像附加的噪声主要是条带噪声,表现为图像中灰度变化缓慢的明暗相间竖条纹分布。本文的图像恢复在频域中进行,因此,选择在频域进行图像去噪处理。对图像进行傅里叶变换时,条带噪声在频谱图上表现为频域横轴上按一定规律分布的亮点。采用频率域陷波滤波器来消除图像中的条带噪声[7-8],过滤掉傅里叶频谱中对应条带噪声的高频成分,然后,进行傅里叶反变换即可得到去噪后的图像。图1( a) 是截取的部分遥感图像,分布有明显的垂直条带噪声,其对应的频谱图为图2( a) ;图1( b) 是通过陷波滤波器进行去噪处理后的图像,其对应的频谱图为图2( b) 。通过两图对比可见,本文选取的去噪方法基本除去了图像的条带噪声,有效地改善了图像质量。

图1 图像条带噪声去除Fig.1 Removing strip noise of images

图2 图像频谱图Fig.2 Fourier spectrum of the images
3.2 PSF 估计与拟合
目前主要用3 种方法估计系统的PSF:
(1) 使用带有特征地物的图像( 例如飞机跑道、桥梁或人工靶标图像) 估计PSF;
(2) 高分辨率图像对比法,需要卫星上载有分辨率不同的多种成像仪;
(3) 根据系统设计标准和系统分析模型[9]推算PSF。
本文采用第一种方法,利用刀刃法估计成像系统的PSF。
由于获取遥感图像的条件复杂,直接估计得到的PSF 误差很大,本文采用高斯拟合对直接估计的PSF 进行校正,使其更符合实际的成像系统。
刀刃法是选取图像中具有一定灰度差异的相邻两块地物边界作为刀刃边缘图像,两块边界的灰度变化要均匀,并与轨道方向具有一定的倾角[10],原理如图3 所示。详细步骤如下:
(1) 从图像中抠取具有刀刃边缘特征的子图像,对子图像每一行提取边缘分界点;
(2) 采用最小均方误差线性拟合边缘分界点,得到边缘分界线,并以分界线与每一行的交点作为新的分界点;
(3) 计算子图像每一行上的其他像素相对于分界点的偏移量,并以0.05 的分辨率( 每两个数据中插入20 个数据) 对偏移量数据进行3 次样条插值;
(4) 插值后所有行的偏移量数据取平均,得到子图像的边缘扩散函数( ESF) ;
(5) 对边缘扩散函数微分得到线扩散函数( LSF) 。
对于推扫式TDI-CCD 相机,沿轨方向和跨轨方向的不对称性很小,成像系统PSF 可以分解为沿轨和跨轨方向的两个一维分量,分别对应于沿轨和跨轨方向的LSF,用沿轨方向的LSF 列向量乘以跨轨方向的LSF 行向量,得到二维PSF。
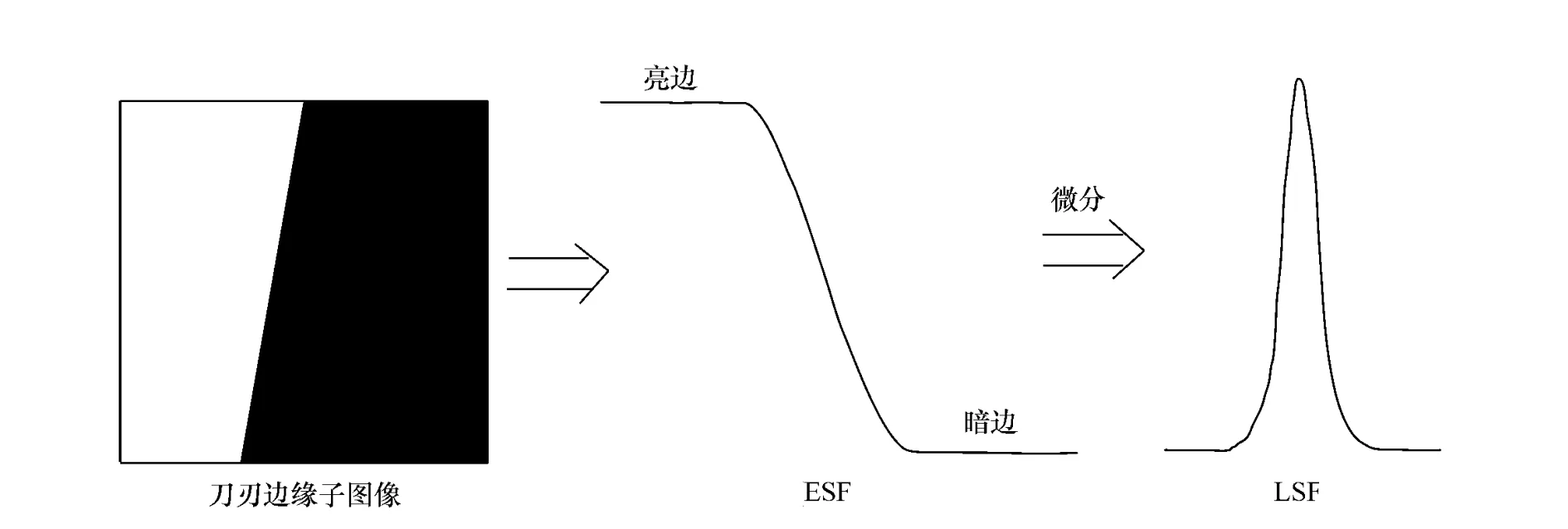
图3 刀刃法原理图Fig.3 Schematic diagram of knife-edge method
成像系统的PSF 趋向于高斯型,可以表示为:

式中,σx,σy为标准差。PSF 在沿轨和跨轨两个方向是可分的,即:

从图3 中LSF 的形状可见它近似为高斯型[11],但并不完全符合高斯表达式。为了减少PSF 估计的误差,对得到的LSF 曲线进行高斯拟合,使用拟合后的数据形成PSF 离散矩阵。
3.3 图像恢复
遥感图像具有数据量庞大的特点,对其进行恢复的时间代价相对较高。因此,估计出成像系统的PSF 后,选择维纳滤波进行图像恢复。维纳滤波性能好,没有迭代过程,比Lucy-Richardson算法和正则滤波运算量少,能够以很低的计算代价获得较好的复原效果,其频域表达式可简化为:
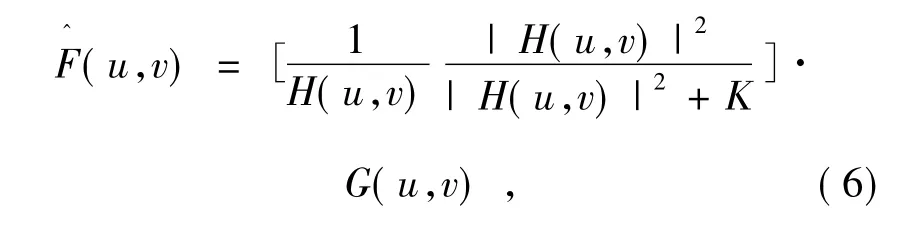
式中:H(u,v) 为高斯拟合后PSF 的二维傅里叶变换,K为恢复过程中的规整化值。
维纳滤波采用固定的规整化值对整个图像进行恢复。较小的规整化值能突出图像的边缘特征,但在图像的灰度连续区域中会产生寄生纹波,影响图像恢复的效果。因此,这里对维纳滤波进行了改进,采用自适应维纳滤波算法进行图像恢复。自适应维纳滤波算法采用Sobel 算子对图像进行边缘检测,把图像划分为边缘特征区域和灰度连续区域,在边缘特征区域使用较小的K值,突出图像细节的恢复; 在灰度连续区域用较大的K值,避免产生寄生纹波。
遥感图像中包含条带噪声,在图像恢复之前进行了有效的去噪处理。通过选取图像中具有刀刃边缘特征的地物估计拟合PSF,然后,分别采用维纳滤波和自适应维纳滤波对整幅图像进行了恢复处理。图4( a) 是截取了遥感图像中的一个铁塔顶部,其上分布有垂直的条带噪声。图4( b) 是应用维纳滤波对去噪处理后的图像进行恢复处理的结果,由于进行了去噪预处理,条带噪声的影响非常弱,频域恢复中没有受到增强噪声的影响。可见去噪处理消除了图像中的高频条带噪声,有效地增强了图像恢复的效果。由于维纳滤波固有的不足,图4( b) 相对于图4( a) 虽然有一定效果,但由于存在寄生纹波,整个图像的清晰度还不够。图4( c) 是采用自适应维纳滤波算法进行恢复的结果,由于对不同的图像区域采取不同的规整化值进行恢复,因此,恢复后图像的细节更加突出,图像清晰度得到增强。图5( a) 是具有复杂地形的遥感图像,图5( b) 是先去除条带噪声,然后采用自适应维纳滤波算法进行恢复的结果。原图中明显的条带噪声经过去噪后基本消除,没有影响最终恢复图像的效果。

图4 遥感图像去噪与恢复Fig.4 Denoising and restoration of remote sensing images

图5 复杂图像自适应维纳滤波恢复Fig.5 Adaptive Wiener filtering restoration for complex images
4 遥感图像恢复效果评价
4.1 图像质量评价标准
除了在主观上通过人眼观察评价上述遥感图像恢复效果外,还应引入客观评价标准,对图像的恢复效果进行定量分析。图像恢复消除了图像的模糊现象,与原图相比恢复图像细节丰富,表现为相邻像素的灰度变化较大,具有更大的梯度值,相关的图像梯度函数可作为评价图像恢复效果的标准,具体如下:
(1) 方差:图像的方差大,说明图像灰度层次较为丰富。M、N为图像的高度和宽度,f(i,j) 为图像某点的灰度值,u为图像的灰度均值,u =
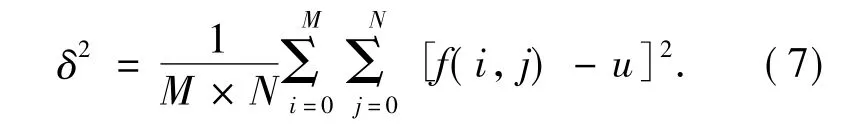
(2) 灰度平均梯度: 反映图像在水平和垂直方向的灰度变化。灰度平均梯度越大,表明图像越清晰。其中:
灰度平均梯度计算公式为:
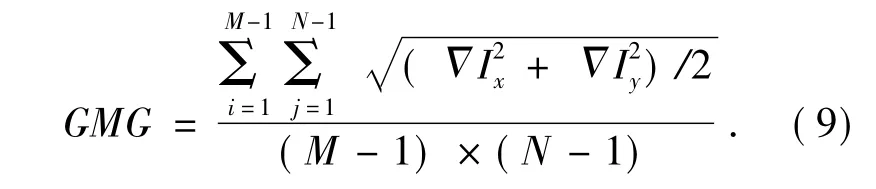
(3) Laplacian 梯度: 反映图像每一像素附近的灰度变化。Laplacian 梯度值越大表明图像轮廓越鲜明,相应地图像越清晰。其中:

4.2 图像恢复效果评价
由图4 可见,待处理的遥感图像细节不清,铁塔的支撑结构边缘非常模糊。表1 的数据也验证了这一点,未恢复之前的图像各项评价标准值均比恢复后的图像低很多。由于图像恢复处理增强了图像细节和边缘特征,由表1 可见,恢复后图像的方差和灰度平均梯度明显增大,表明恢复后图像包含的信息更多,图像更清晰。结合表1,对比图4( b) 与图4( c) 的恢复效果可见,自适应维纳滤波比直接维纳滤波的恢复图像清晰程度高,各项指标均有很大提高,采用维纳滤波恢复后方差比原图4( a) 方差增大1.866,灰度平均梯度增大1.289,Laplacian 梯度增大8.21;采用自适应维纳滤波恢复后,图4( c) 方差比原图4( a) 方差增大4.395,灰度平均梯度增大1.799,Laplacian梯度增大10.014,说明采用自适应维纳滤波算法可以获得更好的图像恢复效果。对图5 所示的复杂遥感图像,自适应维纳滤波同样取得了很好的恢复效果。由表2 可知,恢复后图像方差比原图方差增大20.753,灰度平均梯度增大1.766,Laplacian 梯度增大5.018。

表1 遥感图像恢复评价Tab.1 Evaluation of remote sensing image

表2 复杂遥感图像恢复评价Tab.2 Evaluation of complex remote sensing image
5 结 论
针对航天遥感相机成像过程中图像退化作用引起的图像模糊,提出了高斯拟合的PSF 估计方法,并采用自适应维纳滤波进行图像恢复。考虑图像恢复过程会放大噪声,因此,在恢复之前先对图像进行去噪预处理,采用频率域陷波滤波器消除了遥感图像中附加的条带噪声。去噪后,根据所处理遥感图像的特点,利用图像中的特征地物,采用刀刃法估计成像系统的点扩散函数PSF,为了保证PSF 估计的精度,对刀刃法得到的PSF 进行高斯拟合,将拟合后的PSF 应用到自适应维纳滤波中进行图像恢复。实验结果表明: 去噪处理有效地消除了图像中的条带噪声,自适应维纳滤波比直接维纳滤波取得了更好的图像恢复效果。细节图像经自适应维纳滤波恢复后方差比原图方差增大4.395,灰度平均梯度增大1.799,Laplacian 梯度增大10.014; 复杂图像经自适应维纳滤波恢复后,方差比原图方差增大20.753,灰度平均梯度增大1.766,Laplacian 梯度增大5.018。恢复后图像中的细节更清晰,特征更易识别,利于图像的判读和分析。
[1] 许元男,赵元,刘丽萍,等.含噪声模糊图像的点扩展函数参数辨识[J].光学 精密工程,2009,17(11) :2849-2856.XU Y N,ZHAO Y,LIU L P,et al.. Parameter identification of point spread function in noisy and blur images[J].Opt.Precision Eng.,2009,17(11) :2849-2856.( in Chinese)
[2] 郭永彩,王婀娜,高潮.空间自适应和正则化技术的盲图像复原[J].光学 精密工程,2008,16(11) :2263-2267.GUO Y C,WANG E N,GAO CH. Blind image restoration algorithm based on space-adaptive and regularization[J].Opt.Precision Eng.,2008,16(11) :2263-2267.( in Chinese)
[3] 江洁,邓琼,张广军.基于小波变换的正则化盲图像复原算法[J].光学 精密工程,2007,15(4) :582-586.JIANG J,DENG Q,ZHANG G J. Regularization algorithm for blind image restoration based on wavelet transform[J].Opt.Precision Eng.,2007,15(4) :582-586.( in Chinese)
[4] 顾行发,李小英,闵祥军,等.CBERS-02 卫星CCD 相机MTF 在轨测量及图像MTF 补偿[J].中国科学E 辑 信息科学,2005,35:26-40.GU H F,LI X Y,MIN X J,et al.. On-orbit MTF Estimation and MTF compensation of CCD camera in CBERS-02 satellite[J].Science in China,Series E Information Sciences,2005,35:26-40.( in Chinese)
[5] 陈强,戴奇燕,夏德深.基于MTF 理论的遥感图像复原[J].中国图像图形学报,2006,11(9) :1299-1305.CHEN Q,DAI Q Y,XIA D SH. Restoration of remote sensing images based on MTF theory[J].J. Image and Graphics,2006,11(9) :1299-1305.( in Chinese)
[6] 张朋,刘团结,王宏琦.线阵CCD 相机MTF 的系统模型估计法与图像复原[J].光学技术,2009,35(3) :394-398.ZHANG P,LIU T J,WANG H Q. MTF estimation based on system modal for linear CCD camera and image recovery[J].Opt. Technique,2009,35(3) :394-398.( in Chinese)
[7] GONZALEZ R C,WOODS R E. 数字图像处理[M].2 版.北京:电子工业出版社,2007.GONZALEZ R C,WOODS R E.Digital Image Processing[M]. 2nd ed. Beijing:Publishing House of Electronics Industry,2007.( in Chinese)
[8] GONZALEZ R C,WOODS R E,EDDINS S L. 数字图像处理:MATLAB 版[M].北京:电子工业出版社,2005.GONZALEZ R C,WOODS R E,EDDINS S L.Digital Image Processing Using MATLAB[M]. Beijing:Publishing House of Electronics Industry,2005.( in Chinese)
[9] BENSEBAA K,BANON G J F,FONSECA L M G. On-orbit spatial resolution estimation of CBERS-1 CCD system from bridge images[C]. Proceedings of the XXth International Society for Photogrammetry and Remote Sensing( ISPRS) ,Istanbul,Turkey,July 2004:36-41.
[10] CHOI T. IKONOS satellite on orbit Modulation Transfer Function( MTF) measurement using edge and pulse method[D]. Brookings:South Dakota State University,2002.
[11] 周松涛,宣家斌.基于景物灰度分布特征的影像恢复技术[J].武汉测绘科技大学学报,1999,24(3) :230-234,239.ZHOU S T,XUAN J B. Restoration technique based on image features[J].J. Wuhan Technical University of Surveying and Mapping,1999,24(3) :230-234,239.( in Chinese)

