蒙特-卡罗法计算黑体空腔有效发射率

方茜茜，方 伟 王 凯

(1.中国科学院 长春光学精密机械与物理研究所，吉林 长春130033;2.中国科学院 研究生院，北京100039)

1 引 言

黑体空腔的有效发射率在光度学、辐射度学等领域具有重要的应用。有效发射率与腔的几何尺寸、内表面的光学性质、腔壁温度分布以及观察条件密切相关。从20 世纪60 年代开始，科学家便通过实验测量的方式确定黑体空腔的有效发射率［1-5］，由于辐射收集不完全、腔体温度等重要参数测量不准确、应用不方便等因素，实验测量并不是得到黑体空腔有效发射率的有效手段，而同步发展起来的理论计算方法克服了上述困难［6-8］。20 世纪80 年代，随着计算机的广泛应用，蒙特-卡罗方法开始应用于辐射热传递等领域。该方法的优点是易于处理复杂的空腔形状和壁面辐射特性，物理解释清晰，便于计算机处理，且不存在收敛性问题，所以是计算黑体空腔发射率的有效方法。对于任意形状、内表面光学性质均一( 内表面可能是均匀漫反射、镜面反射或者均匀漫-镜反射) 的等温和不等温腔体，该方法均取得了较好的结果［9-13］。

1973 年，Heinisch［14］首次将蒙特-卡罗法应用于圆锥形腔的半球有效发射率的计算，其研究重点是腔内光线追迹算法、不等温腔修正项的计算以及如何提高计算速度等。目前，蒙特-卡罗法在计算黑体空腔发射率上已经拥有扎实的理论基础和相对固定的算法，并受到国内外相当多研究人员的关注，如清华大学、中国计量科学研究院等单位的研究人员［15-17］在20 世纪90 年代即采用蒙特-卡罗法对圆锥腔、圆柱腔、带锥底的圆柱腔等不同形状的黑体空腔进行了有效发射率计算，并通过优化随机数产生算法，添加环境辐射修正、不等温修正等得到了较好的计算结果，但在蒙特-卡罗法的物理思想和光线追迹算法上基本沿用国外的理论。目前，随着计算机硬件的发展，蒙特-卡罗法的计算速度与以前相比得到很大提高，算法本身也得到进一步的完善和优化，但基本的光线追迹思想仍保持不变。随着计算机软件技术的迅速发展和广泛使用，不仅能通过编程实现光线追迹算法，还可以使用optiCAD，Tracepro 等软件实现，使得蒙特-卡罗方法的实施过程变得更加便捷。本文具体阐述了运用蒙特-卡罗法计算黑体空腔有效发射率的物理基础和两种光线追迹算法，讨论了两种光线追迹思想的利与弊，对前人的工作进行了总结，为今后的研究提供参考。

2 黑体空腔的有效发射率

为了简化运算，近似认为腔体内表面的光学性质均一，与位置和波长无关。对均匀的漫-镜反射模型做了如下近似:

(1) 半球反射率是指由某一方向入射的光在半球空间内的反射率，它由镜面反射ρs和漫反射ρd两部分组成( ρ=ρs+ρd=1 -ε) ，近似认为半球反射率ρ 不依赖于入射角。

(2) 表面漫反射率定义为D=ρd/ρ，也不依赖于入射角。

对于任意形状的腔体，从腔口径出射的光谱辐亮度随方向变化而变化。温度为T0的等温腔的光谱定向有效发射率定义为:

式中:Lλ( λ，T0，ξ，ω) 为腔壁ξ 点沿ω 方向在波长λ 处的光谱辐亮度，Lλ，bb( λ，T0) 为理想黑体在相同温度和波长处的光谱辐亮度。对于等温灰体腔，εe( ξ，ω) 只与腔体的几何形状、光学性质以及出射条件有关，与波长无关。

对于轴对称黑体空腔，观察方向平行于腔体的轴线并与腔体口径相交于坐标(x，y) 时的定向有效发射率被称作垂直有效发射率εe，n(x，y) ，它是定向有效发射率的特例。

另一个重要的物理量是积分有效发射率。在距离腔体口径Hd处放置一个半径为Rd的共轴探测器，积分有效发射率是由温度为T0的腔体发出，入射到探测器上的光谱辐射通量Φλ( 或总辐射通量Φ) 与和腔口径面积相同、温度相同的理想黑体辐射到相同探测器上的光谱辐射通量Φλbb( 或总辐射通量Φbb) 的比值。

对于等温灰体腔:

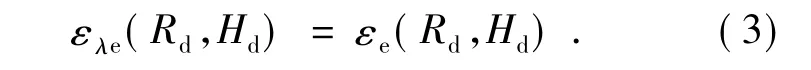
平均垂直有效发射率可以认为是当Hd→∞，Rd=Ra时的积分有效发射率。

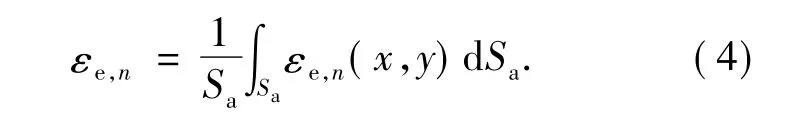
Hd=0，Rd=Ra时的积分有效发射率定义为腔的半球有效发射率。

3 热辐射物理基础

黑体空腔的各个有效发射率都直接或间接地与定向有效发射率相关，垂直有效发射率是入射光线平行于腔体轴线的定向有效发射率，对垂直有效发射率在整个腔体孔径上积分就可得到平均垂直有效发射率，从后面的讨论中还可以看到，对定向有效发射率积分还可以得到半球有效发射率。

在计算中求得定向有效发射率具有很重要的意义。A.Ono 曾在文献［10］中进行详细的理论推导。

图1 所示为面元dx1和dx3通过任意面元dx2进行辐射交换的情况。反射率r1，32表示从dx1方向入射，经面元dx2反射到dx3方向单位立体角的反射率，θ12 表示面元dx2的法线与dx1和dx2中心连线之间的夹角，θ32 表示面元dx2的法线与dx2和dx3中心连线之间的夹角，由相互性原理可得:

图1 面元x1和x3通过中间表面x2的辐射热交换Fig.1 Radiation heat exchange between surface element x1 and x3 through x2

定向半球反射率r1

2 定义为由面元dx1发出经过dx2反射到半球空间的反射率。

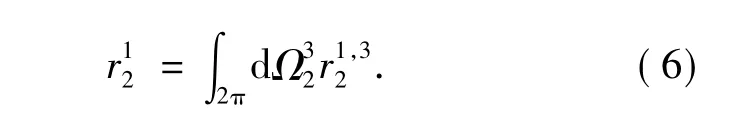
对于不透明体，由基尔霍夫辐射定律得到:

式中，e1

2 是由dx2向dx1方向的辐射通量与相同面积、相同温度的黑体在相同方向的辐射通量的比值，称为定向有效发射率。

任意形状，开口面积为A的等温腔如图2 所示，观察方向为D，则由x0处发出到达D方向的定向光辐射通量为:

图2 任意形状的等温腔体Fig.2 Isothermal cavity with arbitrary shape

式中，Lb是理想黑体的辐亮度。dΦD0 由面元dx0直接发射至D方向以及经x0反射到立体角两部分辐射通量组成。因此:

式中，W是x0可视的所有面积集合。

由式(8) 、(9) 可得定向有效发射率的简化积分方程:

根据相互性原理，上式简化为:

式中，ρD0表示由方向D入射到腔体x0处，并最终反射到半球空间的定向半球反射率。将式( 6) 、(7) 、(11) 带入式(12) 中，可得:

式(13) 的解可以表示为:

式中，fi表示从方向D入射到x0处，经过i次反射射出腔体的辐射量。

在过去的30 多年间，研究人员已经成功地对球体、圆锥、圆柱及组合形状等腔的定向有效发射率进行蒙特-卡罗计算，虽然在具体计算过程中采用的算法不同，但通过对每束光线每次反射出腔口径的辐射量进行求和，用于计算腔的半球反射率，然后由基尔霍夫辐射定律得到腔的定向有效发射率的物理思想是基本相同的。

4 光线追迹算法

光线追迹算法是计算腔体有效发射率的核心。在国际上曾经有正向追迹和逆向追迹两种方法，二者的区别是起始发出光线的位置不同。正向追迹是光线从腔内壁一点发出，然后对光线进行追迹，逆向追迹是光线由腔外观察点发出，当光线入射到腔内部后对光线追迹。由于逆向追迹的思想在计算定向有效发射率时很方便，所以到后期一般都采用逆向追迹的方法。

不等温腔的有效发射率只是在等温情况下做了一些修正，这部分讨论均是针对等温腔，不等温情况将在后面讨论。假设腔内表面是光学性质均匀的漫-镜反射体，反射率ρ=ρd+ρs( ρd为漫反射率，ρs为镜面发射率) 。

4.1 逆向光线追迹

逆向光线追迹是光线由腔外观察点发出，入射到腔内后对光线追迹。该方法可以方便地计算定向有效发射率，经过积分运算后可以得到平均垂直有效发射率和半球有效发射率。

逆向光线追迹的算法一般分为以下4 个步骤:

(1) 假设一束光线从D方向入射至腔的ξ0点，在ξ0处一部分光线被吸收，一部分光线被反射。由伪随机数产生器生成( 0，1) 之间的随机数η，如果η ＜D，则腔体表面发生漫反射，否则发生镜面反射。

如果光线第一次和腔壁相互作用发生镜面反射，则反射光线的方向可以通过下式来确定:

式中，ωi，ωr，n 分别表示入射光矢量、反射光矢量以及腔壁ξ0的法线方向。

漫反射情况稍微复杂一些，近似认为纯漫反射的光能量均匀分布在半球空间中，所以在半球空间随机均匀地产生一个方向代表该束光的漫射方向，如果反射光直接射出腔体，则结束该束光的追迹，否则继续对该束光线追迹。

在半球空间中同等概率地产生漫射方向可以归结为在半球上均匀地产生一点，该点的坐标就可以作为漫射的方向矢量。Marsaglia［13］曾全面系统地总结了关于在球面上均匀地产生一点的问题，他不仅对算法的合理性、可行性予以考虑，还从计算速度、收敛特性上进行了讨论。通常采用的算法也是最容易理解的算法，即是在( -1，1)之间随机产生3 个数时，球面上随机点的坐标为:

Marsaglia 提出了一种新的方法，基本思想是在球体z轴上任意选取一点，过该点作平行于xy面的平面，该平面与半径为1 的球的交线是半径为的圆周。在圆周上随机产生一点。具体算法是产生伪随机数V1、V2∈( -1，1) ，当S=时，球面随机点的坐标为( 2V1( 1 -由于该算法与以往相比减少了伪随机数的个数和平方根的运算次数，计算速度提高了约2 倍。

(2) 追迹第一次反射的光线与腔壁作用点的坐标。目前研究人员基本采用相同的算法追迹光线与腔壁作用点的坐标。

式中:Φ(x，y，z) =0 为腔表面方程，ξ0为发出光线的位置坐标，ξ 为作用点位置坐标，ω 为反射方向矢量，t为系数。

(3) 光线第二次和腔壁发生相互作用，重复(1) ～(2) 的分析过程，直到光线射出腔口径或者经多次反射腔内的光能量减小到可以忽略为止。( 假设入射光束总能量是1，多次反射能量衰减为10-5或10-6可结束追迹) 。

(4) 结束本条光束的追迹，进行下一束光的追迹。为了提高蒙特-卡罗法的计算精度，对同一条件入射的情况，一般需要追迹105～107条光束。

根据上述逆向光束追迹过程，可以推导出黑体空腔定向有效发射率的计算方程。Sapritsky［9］给出的方程如下:

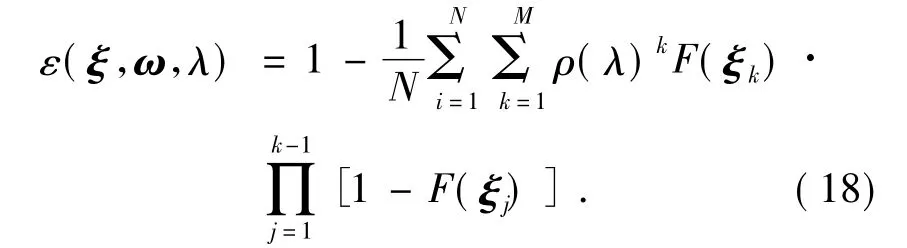
Sapritsky 总共对N条光束进行追迹，其中第i条光束经过M次反射后射出腔体。F是漫反射角因子，具体表达式如下:

式中:Ω 表示ξ 与腔口径所成的立体角; θξ是腔壁ξ 处的法线与立体角dΩ 轴线之间的夹角。F是漫反射光通过腔口径射出腔体的部分。

由此可以看出，Sapritsky 认为每一条光束只要经历一次漫反射，能量就减小1 -F( ξ) 倍。这对镜面反射也是成立的，如果光束经镜面反射刚好射出腔体，则F( ξ) =1，否则F( ξ) =0。

Prokhorov［11］采用更简单的算法:

上式各物理量的含义同式( 18) ，只是Prokhorov 将漫反射和镜面反射同等对待，只是在确定两者的反射方向上有所区别。

4.2 正向光线追迹

正向光线追迹可以方便地计算具有漫-镜反射表面腔的半球有效发射率。Heinisch［14］曾采用正向追迹方法较精确计算漫反射等温圆锥形腔的半球有效发射率。这里将计算推广到任意形状、具有漫-镜反射表面的等温腔:

(1) 腔壁发出光束的起始点坐标ξ 由伪随机数确定。理想情况下，在趋于无穷次的光束追迹过程中，起始发出光线点的位置应均匀地分布在整个腔壁上。

(2) 从ξ 发出的光能量分为两部分，一部分能量E·Fi直接从腔口射出，另一部分能量E(1 -Fi) 在腔内沿随机方向(Rθ、Rφ) 传播。传至下一点时，光束能量将被随机地吸收或反射，这取决于0 ～1 的随机数Rα，当Rα≤ε 时，能量被吸收，否则光束被反射。反射的能量E(1 -Fi) 再次分为两部分，分别为E(1 -Fi)Fi1和E(1 -Fi) ·(1 -Fi1) 。重复上面的过程直至能量在某一点处被吸收。

(3) 选另一发光点，重复上面的过程。

半球有效发射率的计算方程:

式中:Gi=(1 -Fi)Fi1+(1 -Fi) (1 -Fi1)Fi2+…+(1 -Fi) ( 1 -Fi1)Fi2…( 1 -Fim-1)Fim;m=1，2…表示能量在第m次反射之后被吸收;Fi为第i个发光点所在微元对腔口的角系数;Fim为第i个发光点发出的能量在第m次反射时所在微元对腔口的角系数。

5 有效发射率的计算

上面讲述了采用逆向追迹的方法计算黑体空腔定向有效发射率的具体算法。垂直有效发射率是光束垂直于孔径的特殊定向有效发射率，它的算法和定向有效发射率相同。

积分有效发射率εe(Rd，Hd) 是半径为Rd的圆形探测器共轴放置在与腔口径相距Hd的位置时，由探测器测量得到的腔体发射率。它是计算平均垂直有效发射率和半球有效发射率的基础。

图3 计算积分有效发射率简图Fig.3 Diagram of calculating integrated effective emissivity

Prokhorov［11］给出了积分有效发射率的计算公式，如图3 所示，由探测器接收到的总辐射通量表达式如下:

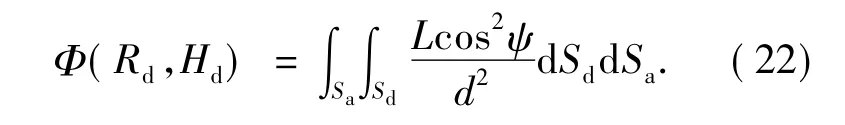
腔口径面元dSa出射的辐射沿ψ 向入射到探测器dSd，L是P点沿PQ方向的辐亮度。如果继续采用逆向光线追迹的方法，认为光线由均匀分布在探测器圆面上的Qi发出，经过均匀分布在腔口径上的Pi点入射到腔体内部，之后的光线追迹过程和上面介绍的定向有效发射率完全相同。那么上面的积分运算可以变为求和运算:

将黑体空腔换为面积为Sa的理想黑体，在相同条件下，探测器接收的辐射通量:

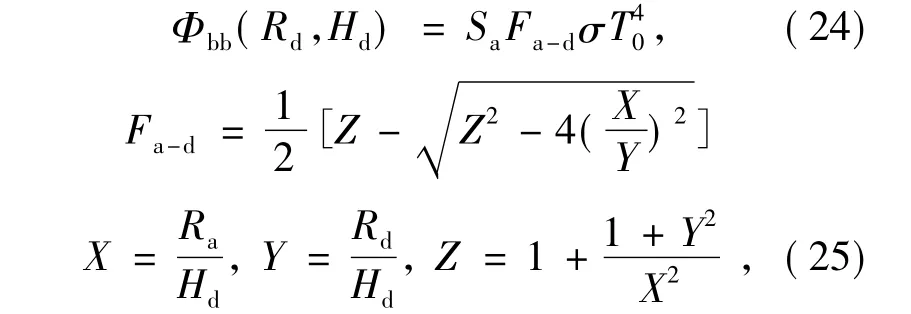
式中，Fa-d为理想黑体对探测器圆面Sd的角系数。

此时黑体空腔的积分有效发射率:

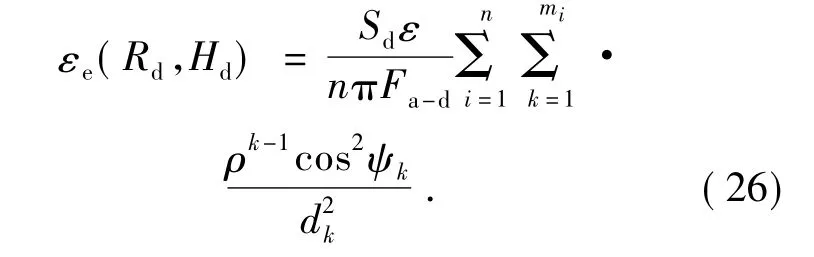
6 不等温腔的定向有效发射率

Sapritsky［9］提出了不等温腔的定向有效发射率，它是在等温情况下加上修正因子，如下所示:

式中:Tξ为腔壁ξ 点的实际温度，T0为参考恒定温度。在逆向光线追迹的过程中，不等温修正项如下:

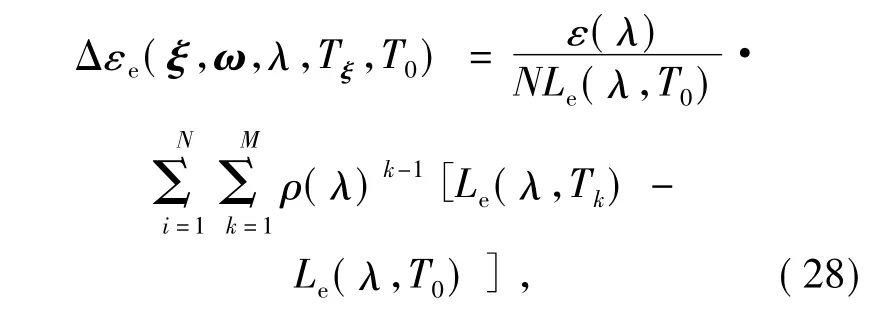
式中:Tk为光线第k次在腔壁上反射时腔壁作用点处的实际温度;Le( λ，Tk) 为温度为Tk，波长为λ 的光谱辐亮度。

7 结 论

本文综述了运用蒙特-卡罗方法计算黑体空腔有效发射率的理论基础和相应的光线追迹算法。不难看出，该方法能够方便、精确地计算黑体空腔的有效发射率。在计算具有漫反射表面的圆柱形腔的积分有效发射率时( 包括半球有效发射率和平均垂直有效发射率) ，得到的不确定度为0.000 1 ～0.000 2，与一些研究人员采用相关理论计算方法得到的不确定度大致相同［18-19］。大部分采用理论计算或者实验测试的方法得到的腔体发射率结果与蒙特-卡罗法得到的结果均符合得很好。目前，蒙特-卡罗方法基本上已经完全取代理论计算的方法，成为获得黑体空腔有效发射率的最主要途径。

［1］ KELLY F J，MOORE D G. A test of analytical expressions for the thermal emissivity of shallow cylindrical cavities［J］.Appl． Opt．，1965，4(1) ：31-40.

［2］ HEINISCH R P，SCHMIDT R N. Development and application of an instrument for the measurement of directional emittance of blackbody cavities［J］.Appl． Opt．，1970，9(8) ：1920-1925.

［3］ BAUER G，BISCHOFF K. Evaluation of the emissivity of a cavity source by reflection measurements［J］，Appl． Opt．，1971，10(12) ：2639-2643.

［4］ BALLICO M. Limitations of the Welch-Satterthwaite approximation for measurement uncertainty calculations［J］.Metrologia，2000，37(1) ：295-300.

［5］ GALAL Y S，SPERFELD P，METZDORF J. Measurement and calculation of the emissivity of a high-temperature black body［J］.Metrologia，2000，37(5) ：365-368.

［6］ BEDFORD R E .Temperature：Its Measurement and Control in Science and Industry［M］. New York：Reinhold Publishing Corp.，1962.

［7］ BARTELL F O，WOLFE W L. Cavity radiators：an ecumenical theory［J］.Appl． Opt．，1976，15(1) ：84-88.

［8］ GEIST J. Theoretical analysis of laboratory blackbodies 1：a generalized integral equation［J］.Appl． Opt．，1973，12(6) ：1325-1330.

［9］ SAPRITSKY V I，PROKHOROV A V. Calculation of the effective emissivities of specular-diffuse cavities by the Monte-Carlo method［J］.Metrologia，1992，29(1) ：9-14.

［10］ ONO A. Calculation of the directional emissivities of cavities by the Monte-Carlo method［J］.J． Opt． Soc． Am．，1980，70(5) ：547-554.

［11］ PROKHOROV A V，HANSSEN L M. Effective emissivity of a cylindrical cavity with an inclined bottom： I. Isothermal cavity［J］.Metrologia，2004，41(6) ：421-431.

［12］ PROKHOROV A V，HANSSEN L M. Effective emissivity of a cylindrical cavity with an inclined bottom：II.non-isothermal cavity［J］.Metrologia，2010，47(1) ：33-46.

［13］ MARSAGLIA G. Choosing a point from the surface of a sphere［J］.The Annals Mathematical Statistics，1972，43(2) ：645-646.

［14］ HEINISCH R P. Radiant emission from baffled conical cavities［J］.J． Opt． Soc． Am．，1973，63(2) ：152-158.

［15］ 张宏.黑体空腔发射率求解中的Monte-Carlo 法［J］.哈尔滨科学技术大学学报，1996，20(3) :72-76.ZHANG H. Monte-Carlo method in calculating the radiant emission of blackbody cavity［J］.J． Harbin University Sci．Technol．，1996，20(3) :72-76.( in Chinese)

［16］ 黄东涛，陆家钦，段宇宁.黑体空腔发射率计算的蒙特卡罗模型［J］.清华大学学报，1997，37(2) :28-31.HUANG D T，LU J Q，DUAN Y N. Monte-Carlo model for calculation of cavity effective emissivities［J］.J． Tsinghua University，1997，37(2) :28-31.( in Chinese)

［17］ 孙富韬.Monte-Carlo 方法在黑体空腔有效发射率计算中的应用［J］.宇航计测技术，2010，30(2) :26-29.SUN F T. Calculation of the effective emissivities of blackbody cavity by the Monte-Carlo method［J］.J． Astronautic Metrology and Measurement，2010，30(2) :26-29.( in Chinese)

［18］ CHEN S，CHU Z，CHEN H. Precise calculation of the integrated emissivity of baffled blackbody cavities［J］.Metrologia，1980，16(2) :69-72.

［19］ CHANDOS R J，CHANDOS R E. Radiometric properties of isothermal，diffuse wall cavity sources［J］.Appl． Opt．，1974，13(9) :2142-2152.