基于相位相关的匀速直线运动模糊图像位移参数估计

孙 辉 ，李志强

(中国科学院 长春光学精密机械与物理研究所，吉林 长春130033)

1 引 言

机载、车载、船载等动载体成像系统工作时，由于载体与目标景物之间的相对运动，相机拍摄的视频图像会产生运动模糊效果，这对图像观察、目标识别造成了困难，同时也为图像信息的处理与分析带来了不利影响。根据图像复原理论，图像运动模糊是一种由成像系统光学模糊造成的视频图像退化现象［1］，结果导致图像质量下降和信息丢失。如何快速准确地从退化图像中获取目标图像运动信息，是目标识别与跟踪的关键技术之一。

图像运动估计主要检测成像系统拍摄的视频图像之间的位移量，目的是从中获取感兴趣区域的目标运动信息，如试验靶场中的飞行目标、工业检测中的零部件、公共交通中的行驶车辆等，同时也为图像的进一步处理与分析( 如图像运动补偿、目标识别、目标跟踪、目标检测、图像变换、图像压缩等) 提供准确参数。目前比较常用的时域空间运动检测方法有图像灰度信息算法［2］、目标特征信息法［3］、图像梯度相关方法［4］等。在运动模糊图像中，由于图像信息的混迭现象，许多有用的特征信息无法从图像中直接获取，因此，上述基于目标特征信息的检测效果会受到严重影响，往往需要通过对图像进行复原处理，根据图像退化模型和光学系统的先验知识恢复原始图像，从恢复图像中获取需要的图像信息。

目前，针对由于运动造成的图像退化方面的研究主要集中在像移补偿［5］、图像恢复或重建［6-7］、点扩散函数估计［8-9］等方面，关于如何从退化图像中获取图像之间的位移参数少有报道。本文从实际需求出发，结合目前广泛采用的相位相关图像配准技术［10-13］和线性不变空间退化模型，通过理论分析和实验验证，讨论了退化图像对相位相关配准结果的影响，将相位相关配准方法应用于匀速直线运动模糊图像之间的运动参数估计，利用相位相关配准技术的高精度和鲁棒性，探索出一条适合检测匀速直线运动模糊图像运动的有效技术途径。

2 相位相关配准原理

相位相关算法最早由Kuglin 和Lines 在1975年提出［14］，它是一种非线性、基于傅里叶功率谱的频域相关技术，具有亚像素级配准精度。该方法只提取两幅图像互功率谱中的相位信息，减少了对图像内容的依赖，具有较强的抗干扰能力，是目前广泛使用的频域配准方法。

根据傅里叶变换平移理论，当图像之间发生平移变化时，傅里叶变换幅值不变，互功率谱的相位等于两个图像的相位差，通过求解归一化互功率谱的傅里叶逆变换，得到二维Dirachlet 冲激函数，其坐标位置给出了两个图像之间的位移量。

设图像尺寸M×N，f1(x，y) 为基准图像，f2(x，y) 为f1(x，y) 平移(x0，y0) 后的位移图像，满足如下关系:

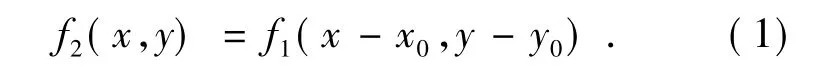
式(1) 傅里叶变换可表示为:

式中，F1(u，v) 和F2(u，v) 分别表示f1(x，y) 和f2(x，y) 的傅里叶变换。因此，两幅图像之间归一化的互功率谱表示为:

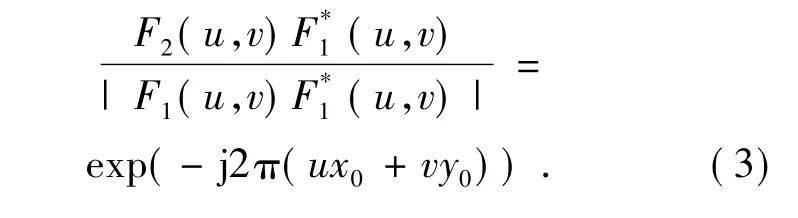
对式( 3) 两端进行傅里叶逆变换，可得相位相关函数表达式如下:

式中:δ(x-x0，y-y0) 即典型的Dirac 冲激函数，该函数在中心点(x0，y0) 处不为零，在其它位置都是零。

为求解位移量(x0，y0) ，文献［7］提出了一种用sinc 函数近似表示Dirac 函数的方法:

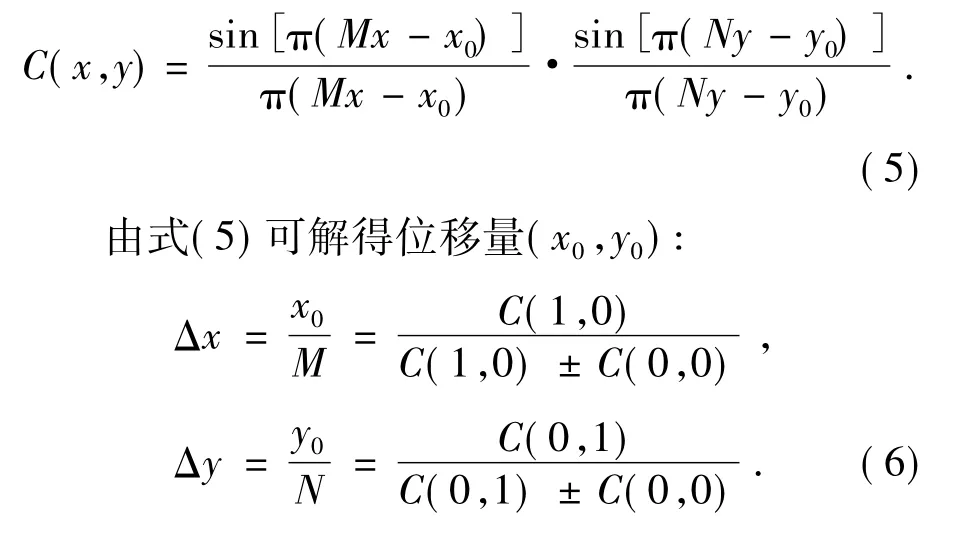
3 匀速直线运动模糊分析

3.1 线性不变空间模糊模型

在线性不变空间退化模型中，f(x，y) 表示物体的原始图像，g(x，y) 表示实际得到的退化图像，h(x，y) 表示点扩散函数( PSF) ，则退化模型可表示为［1］:

将式(7) 两端进行傅里叶变换，有:

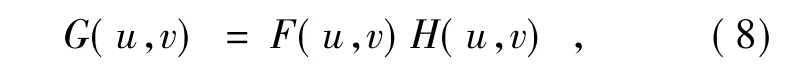
式中，F(u，v) ，G(u，v) ，H(u，v) 分别表示f(x，y) ，g(x，y) ，h(x，y) 的傅里叶变换，其中H(u，v) 在图像处理学中通常称之为转移函数或传递函数。

从式(8) 可以看出，在线性不变空间退化模型中，如果已知点扩散函数或转移函数，就可以通过图像恢复算法求解F(u，v) ，如采用经典的逆滤波、Wiener 滤波等方法，再进行傅里叶逆变换，得到原始图像f(x，y)［5-6］，然后根据实际需要对恢复图像做进一步处理。这种方法虽然有效，但由于在恢复过程中不可避免地会产生误差，对后续的图像处理工作造成一定影响。

本文从线性不变空间退化模型出发，结合相位相关配准算法，进一步研究退化图像对相位相关配准精度的影响，从中找出适合线性不变空间退化图像的运动检测方法。

设g1(x，y) 和g2(x，y) 分别表示式( 1) 中f1(x，y) 和f2(x，y) 的退化图像，则根据式(7) ，有:

将式(1) 代入式( 10) ，建立模糊图像与基准 图像的运动方程如下:

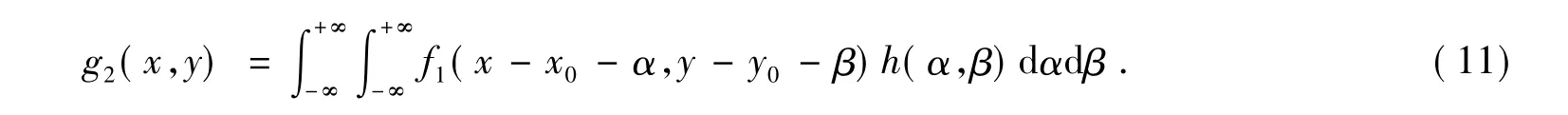
对式(11) 进行傅里叶变换并整理，有:

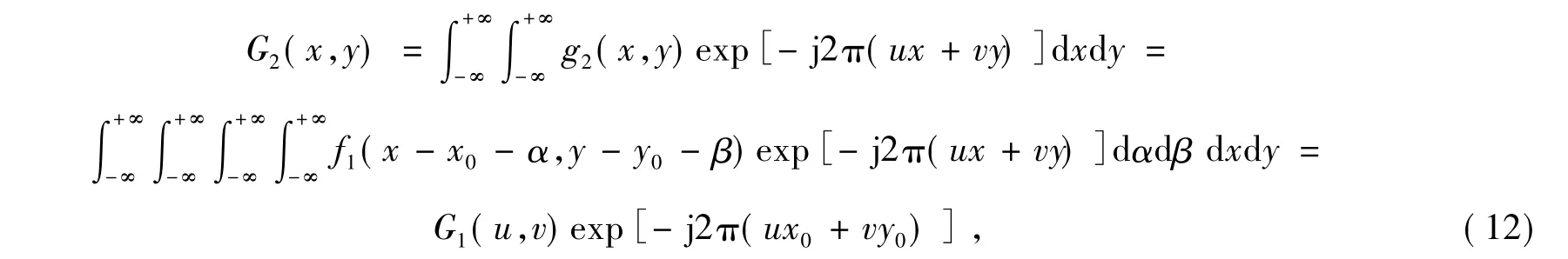
式中，G1(u，v) ，G2(u，v) 分别表示退化图像g1(x，y) ，g2(x，y) 的傅里叶变换。

为进一步研究图像退化对相位相关配准结果的影响，本文根据相位相关配准原理，计算退化图像g1(x，y) 和g2(x，y) 之间归一化的互功率谱。

根据式(12) ，归一化的互功率谱可表示为:

比较式(3) 和式(13) 可知，在线性不变空间退化模型中，退化图像之间归一化的互功率谱与原始图像完全一致，其结果只与图像之间的位移量有关，与图像退化程度无关。利用退化图像的这一特性，可直接从退化图像计算位移图像之间的归一化互功率谱中获取需要的信息。

3.2 匀速直线运动模糊

在动载体成像系统中，由于成像系统与景物之间的相对运动，在相机曝光时间内，目标影像在相机传感器靶面上会产生相应的像移。根据相对运动产生模糊的机理不同，可分为匀速直线运动模糊、斜视运动模糊及旋转运动模糊等［15-16］。其中，匀速直线运动模糊现象在成像系统中比较常见，因此本节进行了相关研究，介绍如何构建点扩散函数和转移函数，进而讨论由此造成的退化现象与线性不变空间退化的关系。

在匀速直线运动模糊中，图像模糊效果与像移的大小和方向有关。在一般情况下，由于曝光时间较短，可以认为在曝光瞬间，载体速度、高度不变，这样产生的图像模糊在连续两幅图像内的模糊程度相同。

设相机与景物之间的相对速度为v，距离( 高度) 为H，相机积分时间为t，相机焦距为f，则像移量δ 可表示为:

式(14) 表明，在成像系统焦距和积分时间一定的条件下，像移量与速-高比成正比。

进一步将δ 表示成像元形式:

式中，M和β 分别表示图像模糊量和传感器尺寸。

根据图像复原理论，图像复原的关键是正确估计成像系统的点扩散函数。在一般情况下，点扩散函数可根据先验知识和实验方法测量估计。本文根据匀速直线运动的特点，参照文献［8］提出的5 种典型的点扩散函数，介绍了一种匀速直线运动点扩散函数及其转移函数的数学描述。

设图像模糊量为M，运动方向与传感器靶面水平方向夹角为θ，则点扩散函数h(x，y) 可表示为:

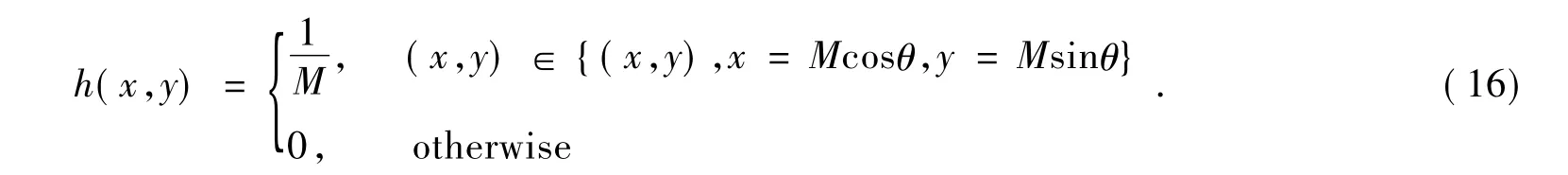
从h(x，y) 定义可以看出，匀速直线运动模糊的点扩散函数是一个二维脉冲响应函数。

根据傅里叶光学理论，成像系统光学传递函数( OTF) 可表示为:

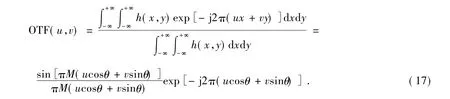
根据运动方向不同，匀速直线运动模糊可分为水平、垂直和斜向3 种，图1( a) ～( c) 分别显示了3 个方向运动模糊的光学传递函数OTF(u，v)曲线。

根据图像复原理论及匀速直线运动点扩散函数或转移函数分析，匀速直线运动模糊符合线性不变空间退化模型要求。因此本文将相位相关配准方法用于解决匀速直线运动模糊图像的运动估计问题具有合理性和可行性，同时可以实现较高的运动检测精度。

图1 光学传递函数OTF( u，v) 曲线Fig.1 Curves of optical transfer function

4 实验结果

4.1 静态仿真实验－归一化互功率谱一致性验证

选用标准样本图像boats 进行位移图像互功率谱一致性测试，原始图像尺寸为512 ×512 ×8 bit，见图2( a) 。首先对原始图像在水平和垂直方向分别平移-20 和10 pixel，生成位移图像，见图2( b) ，然后根据式( 3) 计算两幅图像之间归一化互功率谱，见图2( c) 。

图2 原始图像及位移图像Fig.2 Original image and displacement image

为验证位移图像之间归一化互功率谱经过匀速直线运动模糊前后的一致性，本文进行了对比实验，首先使用式( 9) 和式( 10) 分别对图3 显示的原始图像和位移图像进行匀速直线运动模糊处理，点扩散函数选择式( 16) 表示的方波函数，运动模糊量M=22 pixel，夹角θ=45°。模糊图像见图3( a) 、图3( b) 。然后根据式( 13) 计算两幅模糊图像之间归一化互功率谱，见图3( c) 。

图3 运动模糊图像及位移图像Fig.3 Motion-blurred image and displacement image

比较图2( c) 和图3( c) 可知，模糊图像与原图像的位移图像之间归一化互功率谱具有很好的一致性。

4.2 动态运动估计实验－模糊图像位移量检测

为验证本文方法，在实验室进行了匀速直线运动模糊图像的运动检测实验。实验装置包括光学成像系统、高速数字CMOS 相机，精密转台及计算机等。其中光学系统焦距为150 mm，数字相机传感 器 像 元 尺 寸 为7 μm × 7 μm，帧 频 为25 frame/s，图像分辨率为2 350 ×1 720 ×10 bit，精密转台编码器测角精度为1″。

图像运动量与编码器角度数据关系如下:

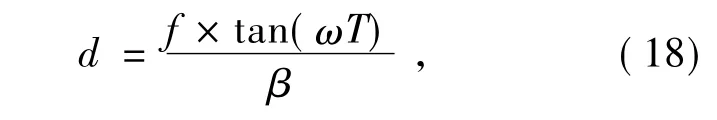
式中:d为位移量;f为光学系统焦距; β 为传感器像元尺寸; ω 为转台角速率;T为视频采样周期。

采用标准差( Standard Deviation，SD) 客观评价运动量计算误差，计算公式如下:

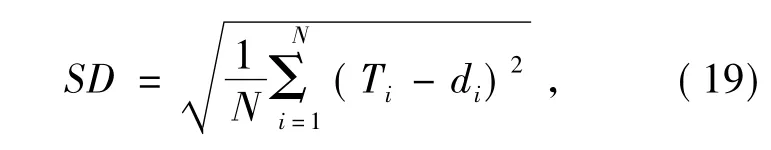
式中:Ti为测试位移，di为根据编码器角度解算的位移真值(i=1，2，…，N) 。

实验采用动态成像方式，通过计算机控制精密转台匀速转动，记录编码器角度数据，用于计算目标图像位移真值。连续采集图像并使用本文方法进行目标图像配准，估计两幅图像之间的位移量。共计采集25 帧图像，采集的序列图像见图4，图像运动量检测曲线见图5，检测误差曲线见图6。

图4 序列图像Fig.4 Sequence of image

从实验结果可以看出，采用本文方法，最大配准误差为0.489，标准差为0.16，配准精度优于1/5 pixel。

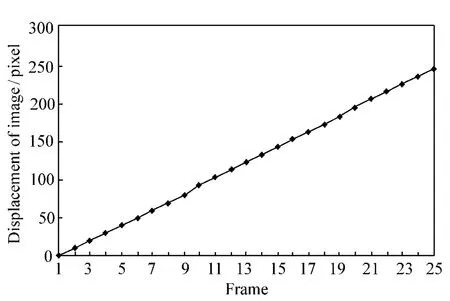
图5 图像运动量曲线Fig.5 Curve of image displacement

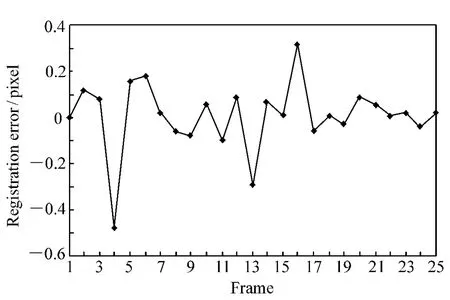
图6 配准误差曲线Fig.6 Curve of registration error

5 结 论

由于载体运动造成的图像退化严重影响目标识别、跟踪及其它信息提取，目前普遍采用的解决方法是图像复原，即通过退化模型和光学系统的先验知识对退化图像进行图像恢复或重建。为进一步提供有用的图像信息，本文通过分析动载体成像系统匀速直线运动模糊的特点，根据相位相关配准原理，结合线性不变空间退化模型，讨论了退化图像对图像配准结果的影响，证明了位移图像之间归一化互功率谱具有运动模糊不变性，为相位相关算法应用于运动模糊图像的运动参数估计提供了理论依据，同时也进一步拓展了相位相关配准技术的适用范围，为匀速直线运动模糊图像的运动参数估计提供了新思路和有效的技术途径。

理论分析和实验结果表明: 相位相关算法在处理运动模糊图像平移方面合理有效，利用图像的互功率谱信息，减少了对图像内容的依赖，具有较强的抗噪能力，同时该算法具有优于1/5 pixel级的配准精度，能有效地提高目标运动的检测精度。

［1］ CASTLEMAN K R.数字图像处理［M］.北京:电子工业出版社，2004.CASTLEMAN K R.Digital Image Processing［M］. Beijing:Publishing House of Electronics Industry，2004.

［2］ KO S J，LEE S H，JEON S W，et al.. Fast digital image stabilization based on gray-coded bit-plane matching［J］.IEEE T． Consum． Electr．，1999，45(3) :598-603.

［3］ 姚军，蒋晓瑜，杜登崇，等.使用粒子滤波器实现电子稳像［J］.光学 精密工程，2009，17(5) :1005-1110.YAO J，JIANG X Y，DU D CH，et al.. Digital image stabilization based on particle filter［J］.Opt． Precision Eng．，2009，17(5) :1005-1110.( in Chinese)

［4］ ARGYRIOU V，VLACHOS T. Sub-pixel motion estimation using gradient cross-correlation［C］//The 7th International Symposium on Signal Processing and its Applications( ISSPA) ，Paris，France，July 1-4，2003.

［5］ LIKHTERIV B，KOPEIKA N S. Motion-blurred image restoration using modified inverse all-pole filters［J］.J． Electronic Imaging，2004，3(2) :257-263.

［6］ 王晓红，赵蓉椿.任意方向运动模糊的消除［J］.中国图像图形学报，2000，5(6) :525-529.WANG X H，ZHAO R CH. Restoration of arbitrary dirction motion-blurred images［J］.J． Image and Graphics，2000，5(6) :525-529( in Chinese) .

［7］ STERN A，INNA KRUCHAKOV，EITAN YOAVI，et al.. Recognition of motion blurred image by use of the method of moments［J］.Appl． Opt．，2002，41(11) :2164-2171.

［8］ STERN A，KOPEIKA N S. Analytical method to calculate optical transfer function for image motion and vibration using moments and its implementation in image restoration［J］.SPIE，1996，2827:191-202.

［9］ TAN K C，LIM H，TAN B T G. Restoration of real-world motion-blurred images［J］.CVGIP，1991，53:291-299.

［10］ FOROOSH H，ZERUBIA J，BERTHOD M. Extension of phase correlation to sub-pixel registration［J］.IEEE T． Image Process．，2002，11(3) :188-200.

［11］ 黎俊，彭启民，范植华.亚像素级图像配准算法研究［J］.中国图象图形学报，2008，13(11) :2071-2075.LI J，PENG Q M，FAN ZH H. Asurvey of sub-pixel image registration methods［J］.J． Image and Graphics，2008，13(11) :2071-2075.( in Chinese)

［12］ 冯林，管慧娟，藤弘飞.基于互信息的医学图像配准技术研究进展［J］.生物医学工程学，2005，22(5) :1078-1081.FENG L，GUAN H J，TENG H F. Advances in medical image registration based on mutual information［J］.J． Biomedical Eng． Res．，2005，22(5) :1078-1081.( in Chinese)

［13］ 桂志国，韩焱.相位相关配准法及其在射线图像数字减影中的应用［J］.仪器仪表学报，2004，25(4) :520-522.GUI ZH G，HAN Y. Phase correlation technique for image registration and its application in DSA of radiographic image［J］.Chinese J． Sci． Instrum．，2004，25(4) :520-522.( in Chinese)

［14］ KULIN C D，HINES D C. The phase correlation image alignment method［C］//Proceedings of the IEEE International Conference on Cybernetics and Society，New York，USA，1975:163-165.

［15］ 李仕，张葆，孙辉.航空多重模糊图像的恢复［J］.光学 精密工程，2009，17(5) :1162-1169.LI SH，ZHANG B，SUN H. Restoration of aerial multiple blurred images［J］.Opt． Precision Eng．，2009，17(5) :1162-1169.( in Chinese)

［16］ WEN C Y，LEE C H. Point spread functions and their applications to forensic image restoration［J］.Forensic Sci． J．，2002，1:15-26.