ASG管脚焊缝超声检测缺陷定位
贺志清,贾志兴
(国核电站运行服务技术公司,上海 200233)
在ASG管脚焊缝超声检测中,受探头、工件结构、焊缝成形等因素影响,会存在缺陷的定位不准的困难,进而影响检测过程及结果。传统绘图法虽然可以解决大部分定位问题,但存在的问题颇多。如传统绘图法需要现场大量时间对焊缝进行取型及测量,增加了检测人员的工作量;传统绘图法对尺寸测量步骤依赖性大,任一环节的疏忽都需要检测人员重复去现场确认,而在核电厂存在辐射风险的特殊环境下,检测人员无法长时间在现场工作。笔者在对国内某电厂ASG管脚焊接件(图1)进行超声波检测时,缺陷在焊缝宽度方向的定位与射线底片存在明显差异。笔者利用改良的作图法找出了声束穿透焊缝的声程范围与声程、探头所处位置三者之间的关系,采用图表形式表示出来,准确确定了缺陷的位置。
1 检测背景及难点
1.1 检测背景
核岛内辅助给水系统(ASG)管道与主给水系统(ARE)管道连接的管嘴焊缝为安放式全焊透管座角焊缝,其现场结构型式见图1。主给水系统和辅助给水系统在核岛较为重要,其安全级别分别为核2级及核2,3级。
1.2 检测难点
受现场条件限制,无法使用射线及内表面超声检测方法对役前检测进行跟踪。笔者在对ASG管脚焊接件进行外表面超声检测时,探头对缺陷的定位在焊缝宽度方向与射线底片之间存在明显差异。究其原因可能是因焊缝表面余高及试件结构所致(图2)。受试件结构影响,超声检测只能进行外表面检测,且现场存在辐射风险,给检测工作造成了一定的困难。
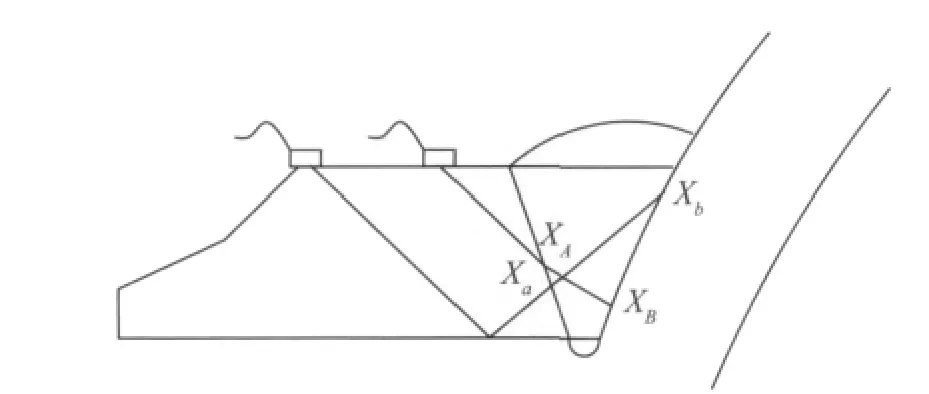
图2 声程范围
2 方法的讨论
2.1 图表方法的讨论说明
现假设探头穿过工件过程中,一次波通过焊缝熔合面所截取的声程范围为XA-XB;二次波通过焊缝熔合面所截取的声程范围为Xa-Xb(图2)。如图所示,当检测中发现异常信号在 XA-XB、Xa-Xb之内时,那么它即为缺陷信号。
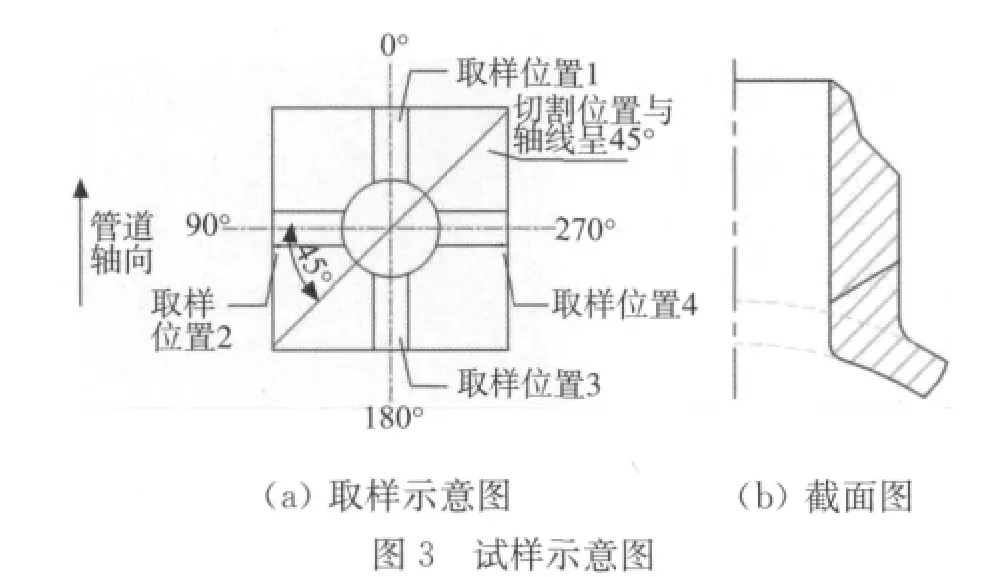
声束在焊缝熔合面内的传播不可见,但探头所处位置的变化可见。而声束在焊缝熔合面内的传播与探头位置之间存在一定关系。管脚焊缝各位置所具焊缝截面图并不一致,如图3所示。现选取90°,270°位置试样示意图,如图3(b)所示。
在对该管脚焊缝进行超声检测时,所使用探头的前沿长度L0=5mm、折射角45°,假设支管侧焊缝外表面边缘为P1点,支管侧焊缝根部边缘为P2点(图4),则探头在扫查过程中存在以下几个基本状态:
(1)位置A 探头前沿紧邻焊缝边缘,超声波以一次波入射,探头入射点O与P1点的最小距离为L0。
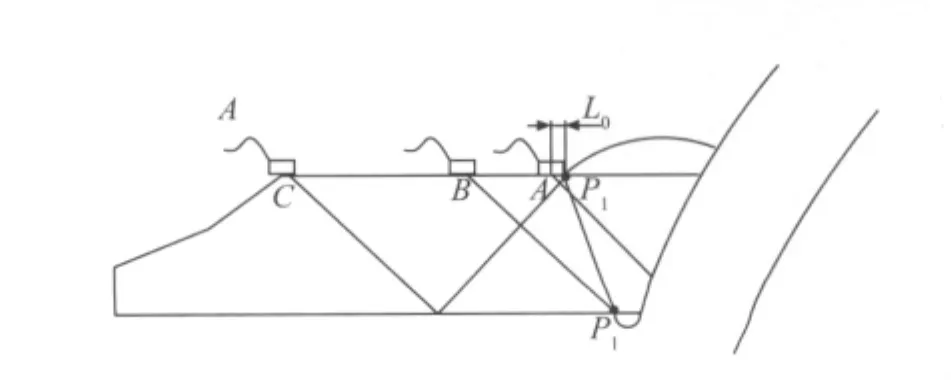
图4 扫查状态
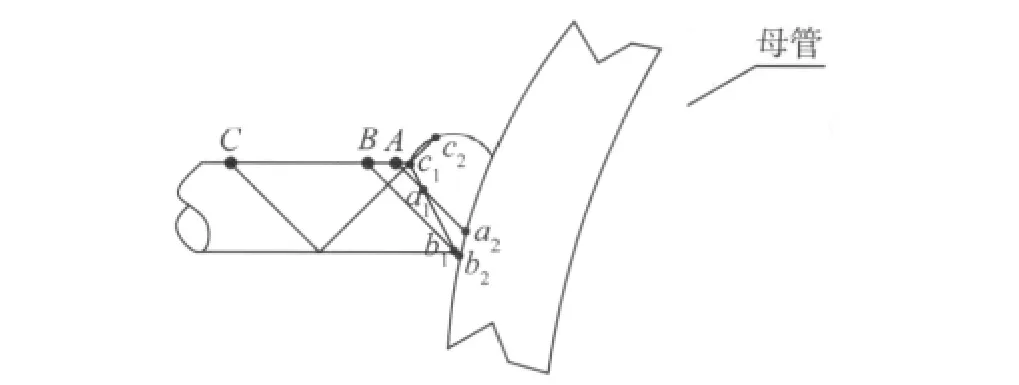
图5 90°和270°位置
(2)位置B 超声波以一次波入射,穿过支管侧母材后到达P2点。
(3)位置C 超声波以二次波入射,穿过支管侧母材后到达P1点。
检测过程中,探头由位置A向远离焊缝侧逐步移动,探头入射点O与P1点的距离L也逐步增大,并且:
(1)探头处于位置A(L=L0)时,按照该管脚焊缝截面尺寸,超声波在焊缝内穿过焊缝熔合面的声程范围为22.13mm。
(2)探头远离位置A向B移动时,超声波均以一次波进行入射,L0<L≤LBP1。
(3)探头远离位置B向C移动时,超声波均以二次波进行入射,LBP1<L≤LCP1。
(4)探头远离位置C以后,超声波以三次波进行入射。
(5)声束不发生改变(探头入射点、入射角度不变)的情况下,L与声束穿过焊缝熔合面的声程(如图2中的 XA-XB,Xa-Xb)存在唯一的对应关系。
2.2 图表方法的应用
现仍采用前沿长度L0=5mm,角度为45°探头,以试件90°,270°位置试样为例。如图5,当入射点为A时,记下探头入射点位置L=L0=5mm,探头入射点至a1的声程表示为O-a1=16.73mm,则O-a2=38.86mm;当入射点为B 时,L=14.96mm,O-b1=50.06mm,O-b2=54.0mm;当入射点为 C 时,L=70.81mm,O-c1=100.12mm,O-c2=118.92mm。以L为横坐标,探头入射点至焊缝熔合面的声程(设为X)为纵坐标,制作曲线如图6。
以L-X 曲线为依据,假设发现一处异常信号,通过测量入射点距离焊缝边缘的距离L,在坐标轴中找到相应的L位置,向上垂直画线,交曲线于A,B两点,找出对应纵坐标数值X1,X2,再读取仪器显示声程值,如声程值在X1-X2之间则为缺陷信号。同时根据缺陷声程值所在X1至X2之间的位置,确定缺陷在焊缝中的位置是偏向主管道侧还是偏向支管侧,或是熔合区中间的缺陷,同样也可判断是否为热影响区的缺陷。缺陷最大回波处的深度也较易得出。使用该方法可减少现场工作时间,方便而直观地给缺陷定位。
2.3 公式法的讨论说明
通过图6可以得知,在一次波和二次波的声程范围中,L与声束穿过焊缝熔合面的声程X分别存在函数对应关系。分别画出该探头一次波及二次波的声程截面图,如图7。
现继续选用45°探头,通过图7(a)可得L/sina=S0-1/sinb。现已知坡口角度,通过计算得a=15°,b=120°;故可得S0-1=L·sinb/sina=3.346L。S1-2=S0-2-S0-1,S0-2为检测中已知,故声束穿过焊缝熔合面的声程X(S1-2)=S0-2-3.346L。即单纯为 X与L的关系。在一次波状态下,就可以采用该公式方便地判断缺陷位置。
继续选用45°探头,已知坡口角度及支管厚度为35mm,同样通过图7(b)可得S0-2=S0-F+SF-1+S1-2;已 知 S0-F=49.5mm,由 三 角 函 数 得 SF-1/sin30°= (35+L-35/tan30°)/sin105°,则 SF-1=(0.5L-12.8)/0.965。S1-2=S0-2-S0-F-SF-1,在S0-2-S0-F已知的情况下,同样可以确定声束穿过焊缝熔合面的声程X与L的关系。
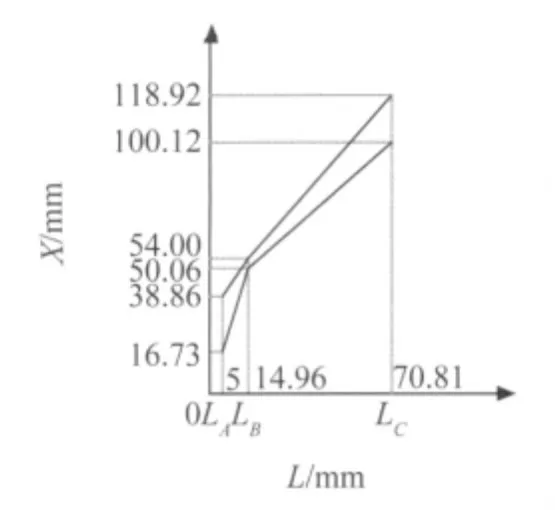
图6 5P6×6的45°探头图表

上述两种方法在实际操作中方便简单,但同样存在不足,该方法中公式及图表仅针对单个角度探头,如需多种角度检测,前期准备较为繁琐。计算法受数值精度影响同样会产生误差。对于检测试件也仅限于对固定角度(以上仅针对270°,90°)位置试件,一般仅对几处典型角度位置试件进行如上曲线制作。其它几处角度与角度之间的缺陷位置坐标图校正则需要大量试验验证。
3 结语
缺陷定位对ASG管脚焊缝的评定很重要,以上方法仅限于固定角度位置试件检测,而角度与角度之间的缺陷位置坐标图校正需要大量试验验证。以上方法都是建立在缺陷的最高回波为探头中心声束上,而在实际工作中受缺陷取向等原因影响,缺陷的最大反射波不一定为探头中心声束所经过,故仍存在超声检测的方法误差。

