涡流传感器检测薄板内气孔型缺陷的三维仿真

谭书涛，陈建钧，潘红良

（华东理工大学 机械与动力工程学院，上海 200237）

涡流检测作为五大无损检测手段之一，操作简单、无需耦合剂、无污染、可在高温环境下作业、快速高效、能实现自动化等优点，被广泛应用于航空、航天、核能、电力、钢铁和石油等行业。它能可靠准确地实现金属板探伤、管材探伤、结构件疲劳裂纹探伤、材料成分的鉴别、热处理状态的鉴别、测量金属薄板的厚度等诸多功能［1］。

涡流检测对缺陷进行定量、定性分析时，一般采用当量比较法，即根据国家制定的探伤标准，用同一规格无缺陷样品在其上按标准刻制一个人工缺陷，然后探头检测该样品并采集信号，该信号在实际检测中作为标准对比信号。通过这种单纯的试验方法去获取数据，存在着成本高、数据少、周期长等缺点。随着有限元方法的广泛应用，涡流检测的电磁学仿真很好地弥补了这些缺点。文章采用三维模型仿真了不同大小、不同深度气孔缺陷的阻抗信号变化。常规涡流检测是一种表面或近表面的无损检测方法，文章模拟的检测对象是2.5mm厚的薄板，通过调整频率大小尽量使涡流渗透到薄板下表面。

1 理论原理及数学模型

1.1 基本工作原理

涡流检测以电磁感应原理为理论基础，对检测线圈中通入正弦交变电流，线圈周围空间将产生交变磁场，置于交变磁场中的导电试件会感应出涡流［2］。由楞次定理可知，此涡流又会产生与线圈磁场方向相反的磁场，进而会部分抵消线圈磁场，导致检测线圈的阻抗发生变化。保持其他条件不变，若导电试件存在缺陷时，试件中涡流的轨迹及强度发生变化，使得线圈相对于无缺陷的阻抗发生变化。检测该变化值便可判断有无缺陷及缺陷大小。

1.2 数学模型

涡流检测与其他电磁场问题一样，都是通过一组麦克斯韦方程组来推导出控制方程。因为检测线圈的激励源为正弦交流电流，控制方程的推导则基于时谐电磁场麦克斯韦方程组，如下：

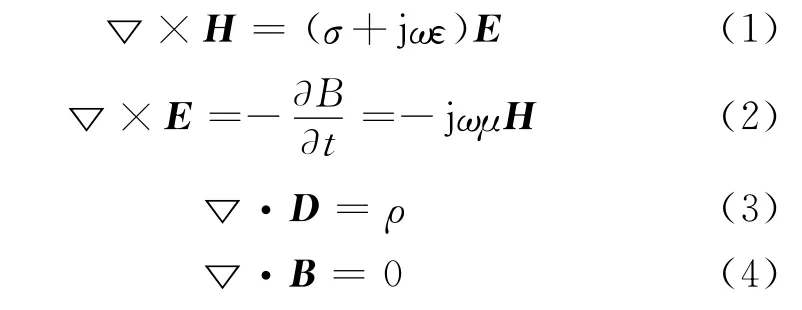
对于各向同性的线性介质，还有三个描述介质性质的方程，如下：

由磁势的旋度等于磁通量的密度，可得如下方程：

把式（5）和（6）代入式（1）方程左边得：

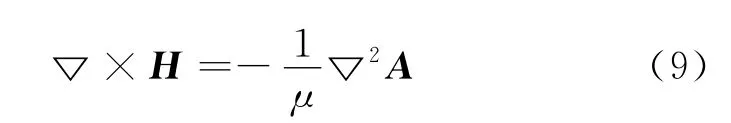
把式（6）代入（2）式可得：

把式（9）和（10）代入式（1）中可得控制方程为：

式中μ表示磁导率；A表示磁失势；ω表示激励电流的角频率；σ表示电导率；ε表示介电常数。

通过有限元方法求解出式（11）微分方程的解，也就是得到存在涡流效应时的磁失势Ae，进而将Ae带入式（12）最右边的式子，求解出检测线圈的阻抗值：

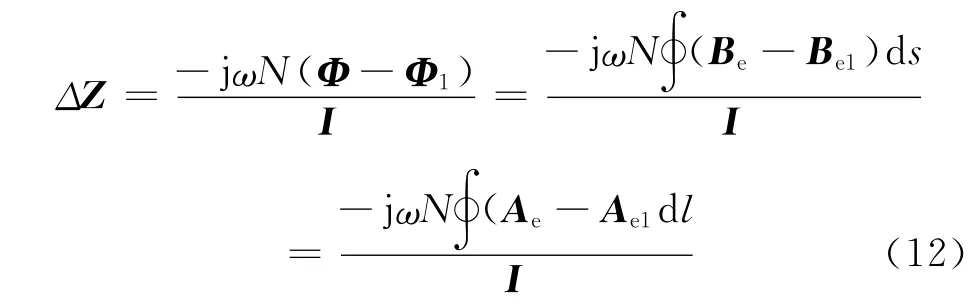
式中ΔZ为线圈阻抗变化值；Ae，Ae1分别为有缺陷和无缺陷时的磁失势；I为线圈通入的有效电流值；Be，Be1分别为有缺陷和无缺陷时的磁场强度；Φ，Φ1分别为每匝线圈有缺陷和无缺陷时的磁通量值。

2 ANSYS－APDL有限元建模过程

ANSYS软件是一款大型通用、功能强大和使用方便的有限元分析软件。它可以进行结构、流体、热、声学和电磁学的计算，而且还可以进行多物理场耦合的计算。文章是基于电路－磁场耦合模块，并采用节点法进行时谐电磁场分析［3］。

2.1 物理模型

图1为涡流探头工作时的二维示意图。被测导体的长宽高为70mm×70mm×2.5mm，气孔缺陷直径为φ，其中心离平板上表面的距离为t。被测导体相对于线圈而言可以认为是无穷大，线圈在缺陷左右两边采集到的阻抗变化值以缺陷中心为中心呈近似对称分布，当线圈到达缺陷中心位置时，阻抗改变值最大，因此在仿真时只需计算线圈位于缺陷中心处的阻抗改变值，就可以反映出缺陷的最大信号值。

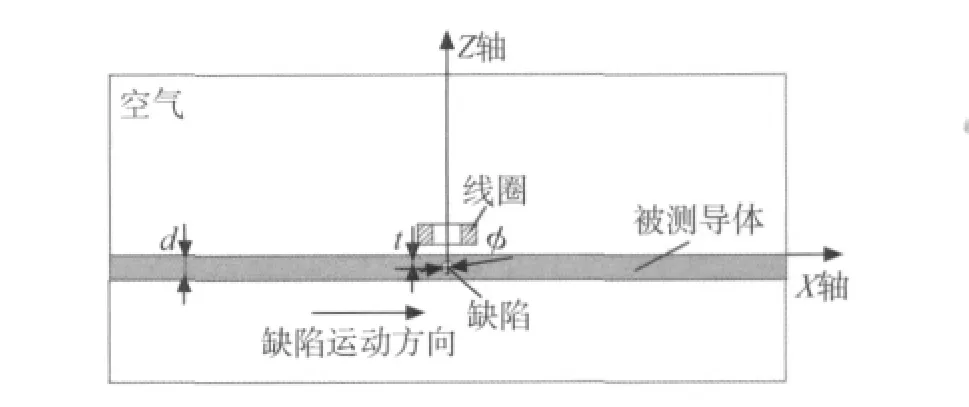
图1 涡流检测内部气孔的二维示意图

2.2 定义单元类型和材料属性

在整体模型中，因采用三维节点法分析，故对线圈、被测导体和空气采用SOLID97实体单元。然后定义CIRCU124电路单元，建立一个独立电流源，并将此电流源与检测线圈耦合，给线圈提供1／140A的电流。被测导体采用铜材料，其相对磁导率μγ＝1，电导率ρ＝1×10e－6（Ω×m）［4］。

2.3 网格划分

在被测导体中由于感应涡流的存在，网格划分时就需要考虑集肤深度的影响，在集肤效应显著的区域应加密网格数。该区域主要是线圈下方包围缺陷的铜板区域，其X轴和Y轴方向的网格精细度要求不高，在Z轴方向应进行精细剖分［5］，故此区域采用映射网格划分，在Z轴方向上薄板的网格层数为7层。上下空气层采用映射网格划分，与线圈和被测导体接触的空气区域采用自由网格划分。划分后的线圈和铜板的网格模型如图2。

图2 线圈和铜板的网格模型

2.4 定义线圈实常数

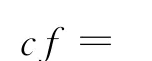
2.5 设置边界条件及加载

文章模型属于第一类边界条件［7］，即令边界面上所有节点的磁失势AX＝AY＝AZ＝0；对线圈加载交变电流时，是通过设置独力电流源的实常数来添加I＝1／140A的电流，以及HARFR命令符来设置加载电流的频率。

2.6 求解及后处理

以上步骤完成后，定义分析类型为谐波分析HARMONIC，并选择稀疏矩阵求解器，执行求解；求解结束后，在通用后处理器POST1中提取实部和虚部结果，以命令符Path定义线圈内的环形封闭路径，Fluxv求解出穿过封闭路径的磁通量，而为了更精确地求解出感应电压，共定义9个封闭路径如图3，取得磁通量的平均值Φ，把Φ代入式（12）求出检测线圈的阻抗改变值。

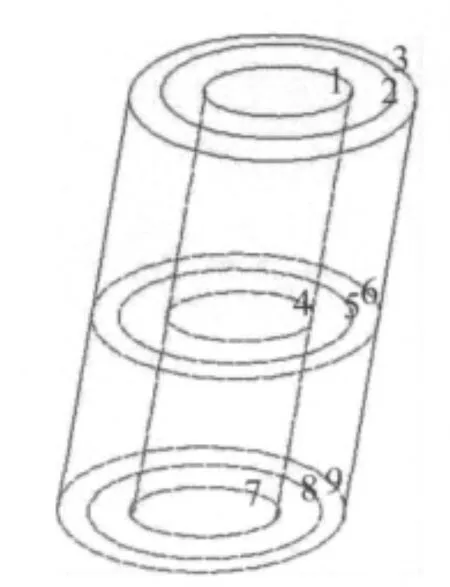
图3 定义的9个封闭路径

3 计算结果分析

3.1 最佳激励频率的确定

在涡流检测时，涡电流的渗透深度和检测灵敏度是一对矛盾。激励频率过高，由于集肤效应的存在，涡电流局限在表面薄层中流动，缺乏有效的检测深度；相反，激励频率过低，会增加渗透深度，但降低了检测灵敏度。因此，寻找满足检测深度和检测灵敏度条件下的最佳激励频率，是涡流检测中一个重要影响因素。

检测目标是直径φ0.4mm的气孔缺陷，其中心与带钢上底面的距离t＝2.1mm。如果能保证灵敏度的情况下检测到该缺陷，那么涡流渗入的深度肯定可以达到铜板的底部。为了能检测到深度为2.1mm的气孔缺陷，选择不同的频率，初步拟定仿真频率范围为1～200kHz。图4为针对存在上述缺陷情况下，采用不同频率，仿真求得阻抗改变值ΔZ的幅值变化趋势。以幅值的大小来衡量信号的强弱。

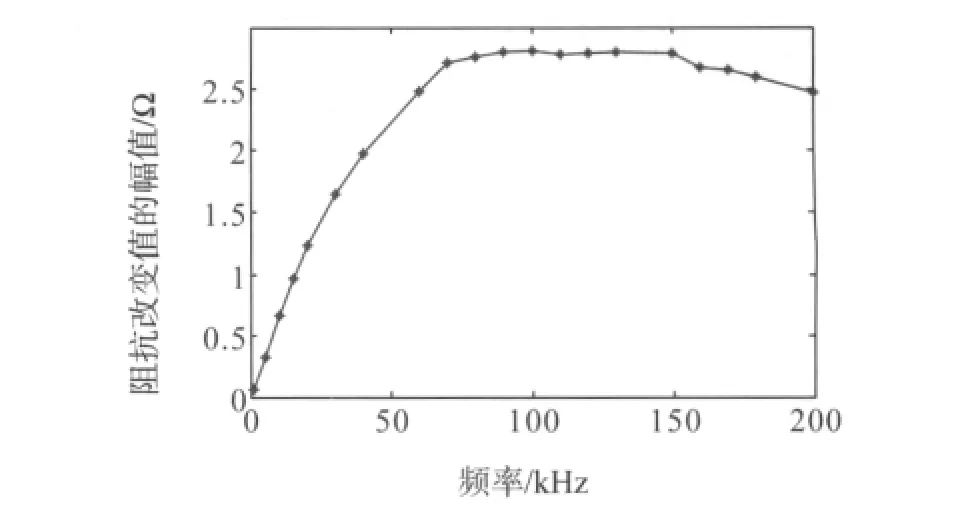
图4 不同频率下ΔZ幅值变化趋势

从图中可以看出，当频率＜80kHz时，信号幅值随着频率的增加而增大；当达到80～150kHz时，信号幅值达到一个最大范围；当超过150kHz后，信号幅值趋于减小。该图形所展现的规律与涡电流的渗透深度和检测灵敏度是一对矛盾相符合。可知当频率达到80kHz左右时，检测灵敏度已达到要求，根据频率越低涡流渗透深度越大来考虑，检测该薄板的最佳频率为80kHz。

3.2 气孔缺陷仿真信号分析

该部分采用的线圈激励频率为80kHz。建模计算时，令气孔直径φ为0.4，0.6，0.8，0.9mm，气孔中心与带钢上表面的距离t为0.6，0.8，1.0，1.2，1.4mm，在每一直径下计算不同t的阻抗变化值。图5（a）为气孔直径φ为0.4，0.6，0.8，0.9mm 时的不同深度位置的信号幅值趋势图，图5（b）为信号相位角趋势图。因为常规涡流检测信号的处理只考虑信号的幅值和相位角，所以在此只研究这两者的规律。

从图5可以看出，当气孔直径一定时，随着气孔中心离上表面的距离越深，阻抗改变值的幅值信号越小，气孔缺陷对涡流信号的干扰越弱；气孔中心离上表面的距离一定时，直径越大，阻抗改变值的幅值信号越大。这种规律与涡流检测原理相符合。从图6的结果可以看出，当气孔中心离上表面的深度值增大时，信号对应的相位角近似呈正比例减小；而在相同的深度位置，不同直径的气孔对应的相位角的大小近似相等。所以通过这个规律可以使用相位角的信息来确定气孔的深度值。

气孔直径φ为0.4，0.6，0.8，0.9mm，气孔中心与带钢上表面的距离t为0.6，0.8，1.0mm，在每一深度距离下计算不同直径的阻抗变化值。图6（a）为深度位置t为0.6，0.8，1.0mm时的不同气孔直径的信号幅值趋势图，图6（b）为信号相位角趋势图。从图6（a）的结果可以看出，在同一深度位置，气孔直径增大时对应的信号幅值也增大。从图6（b）可知，在同一深度位置，气孔直径增大时对应的信号相位角也增大。但在同一深度位置，最大信号相位角与最小相位角的差值＜3°。在此可以充分证明，通过相位角来判断缺陷的深度是完全可行的。

4 结论

通过有限元软件ANSYS模拟了涡流检测薄板内部气孔型缺陷这一过程，求出了检测该铜板的最佳激励频率。在该激励频率下，得出了气孔直径越大、深度越浅，幅值与相位角呈增大趋势，气孔直径越小、深度越深，幅值与相位角呈减小趋势。所得结论与实际理论情况相符合，证实了仿真的可靠性。

［1］冯蒙丽，蔡玉平，赵建君，等.ANSYS在电磁无损检测中的应用［J］.四川兵工学报，2009，30（6）：25－29.

［2］任吉林，林俊明.电磁无损检测［M］.北京：科学出版社，2008.

［3］王晶，潘红良.涡流检测薄板内空气型缺陷的ANSYS仿真研究［C］.全国第九届无损检测学术年会.中国机械工程学会无损检测分会，上海，2010：535－539.

［4］王春兰，张钢，董鲁宁，等.电涡流传感器的有限元仿真研究与分析［J］.传感器与微系统，2006，25（2）：41－46.

［5］Hiroyuki Fukutomi，Toshiyuki Takagi，Junji Tani，et al.Numerical Evaluation of ECT Impedance Signal due to Minute Cracks［C］.IEEE TransMagn，1997，33（2）：2123－2125.

［6］Pingjie Huang，Guangxin Zhang，Zhaotong Wu，et al.Inspection of defects in conductive multi－layered structures by an eddy current scanning technique：simulation and experiments［C］.NDT＆E International，2006（39）：578－584.

［7］孙明礼，胡任喜，崔海蓉.Ansys10.0电磁学有限元分析实例指导教程［M］.北京：机械工业出版社，2007.