Lamb波损伤散射及损伤成像的模拟

李鸿源，徐 鸿，田振华

（华北电力大学 能源动力与机械工程学院，北京 102206）

在航空航天、石油化工、交通运输、能源电力领域内对部件的完整性进行监测和评估十分重要。超声导波检测具有传播距离长的特点，特别适合作为各类部件结构健康监测（SHM）的方法，如金属或复合材料板、管线、铁轨、钢绞线等［1－7］。

Lamb波是存在于板状材料中的导波，具有传播距离远且对损伤敏感的特点，适合对板状构件进行大范围快速检测及在线监测。但是Lamb波同时具有多模态及频散特点，传播过程中，波场较复杂。当Lamb波经过损伤时，在损伤处发生反射、透射、散射及模态转换等，使传播结构发生变化，导波波场复杂性进一步加剧，这将造成损伤特征信号提取困难。因此需要研究Lamb波场与损伤相互作用，以便于损伤识别、特征提取。文章将基于有限元方法，对Lamb波与损伤间的交互作用进行模拟研究。

对于损伤定位，目前已有多种方法，如时间反转法［8］、相控阵列方法［9］及概率的成像方法［10］。文章在分析了Lamb波及损伤波的传播过程的基础上，通过传感器阵列实现对损伤的成像检测。

1 平板中的Lamb波

1.1 Lamb波传播模型

Lamb波是在具有上下界面的波导结构中传播的一种应力波，它是由横波和纵波在上下界面反射、叠加形成的。均质平板中Lamb波特征方程为［11］：

式（1）中p和q分别为：

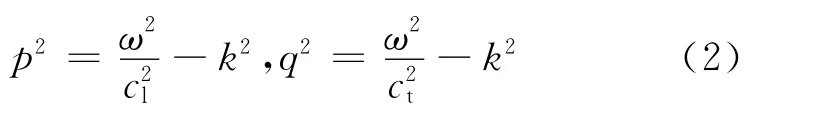
式中h，k，ω分别为平板半壁厚、波数和角频率；cl和ct为材料中纵波及横波的波速；α＝0对应于Lamb波对称模态，α＝π／2对应于非对称模态。

通过对特征方程进行数值求解，可以获得Lamb波频散曲线，如图1所示。通过频散曲线可以看出，Lamb传播具有多模态特点，模态数随频厚积增大而增多；即使在低频区域（A1模态截止频厚积之前），也存在两种Lamb波模态，即A0模态和S0模态。另外，Lamb波传播具有频散特点，即传播速度随频厚积变化而变化，若波包内不同频率成分传播速度不同，将导致波包时域上持续时间随传播距离增加而增长，幅值随传播距离增加而显著降低。

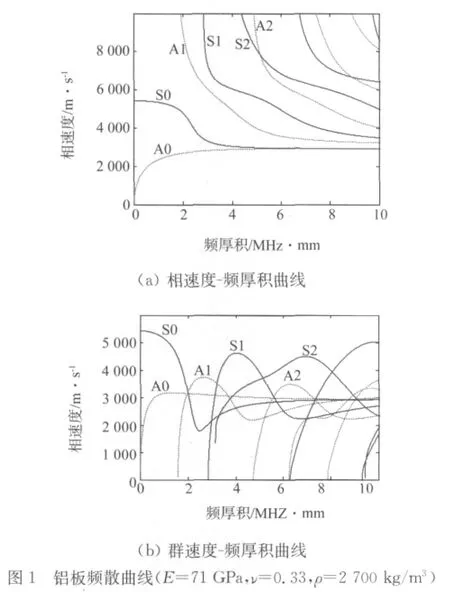
在损伤检测过程中，Lamb的多模态和频散会造成检测信号复杂性增加，难于分析出损伤特征信号。因此在实际应用中，通常需激发单一Lamb波模态作为检测信号，并通过频率选择尽量降低信号的频散。

1.2 Lamb波模态选择

为了控制模态数，超声导波激发频率通常选择在A1模态截止频率以前。在此频率范围内仅存在A0和S0模态。

图2为300kHz下，1.5mm厚铝板中A0和S0模态位移分布。从图2可以看出，A0模态波长相对较短，整个波场以离面位移为主，呈反对称分布；S0模态波长相对较长，整个位移场以面内位移为主，呈对称结构。

在低频区域，S0模态频散较小，传播速度较快，同时其波场以面内位移为主，在外部为液体环境下能量衰减较小。因此选择低频区的Lamb波对称模态（S0模态）作为损伤检测信号。

2 有限元模拟

此处将基于有限元方法研究Lamb波的传播过程，以及损伤对Lamb波传播的影响。

2.1 有限元模型

基于Ansys有限元分析软件，建立了350mm×350mm×1.5mm铝板模型，如图3所示。以铝板中心为坐标原点，在坐标为（50mm，50mm）的D点建立直径为6.35mm的圆形通孔模拟损伤，信号激发点位于坐标为（－25mm，－25mm）的T点，P点为信号提取点。

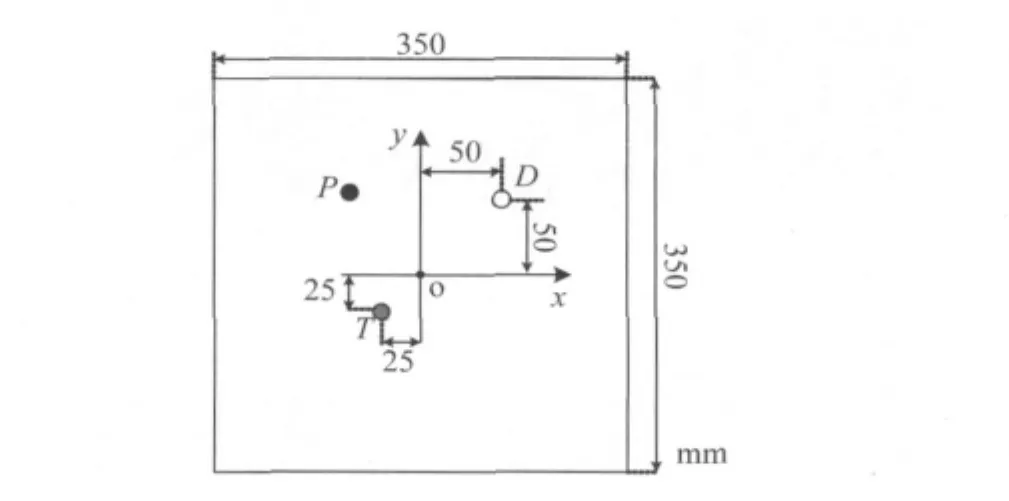
图3 有限元模型示意图

Lamb波传播过程仿真属于瞬态动力学分析，模型单元尺寸和时间步长均会影响计算精度和时间。通常网格尺寸和积分步长需要满足如下关系：

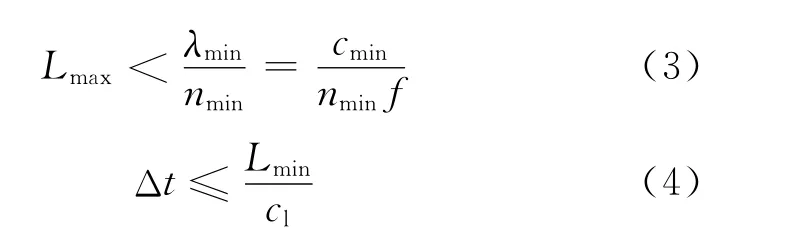
式中Lmax为单个网格上两节点间的最大距离；λmin为最小波长；cmin是Lamb波的最小群速度；nmin是每个波长内的最少网格数，通常取8～10［12］。Lmin，cl分别为最小网格尺寸和纵波波速。根据式（3）和（4），将模型划分为边长1.25mm的solid185单元，时间步长选为0.12μs。

为了在板中激发单一S0模态，在激发点T处上下表面及板内各节点均匀施加面内位移载荷。激发信号采用经Hanning窗调制的5周期正弦波，中心频率为300kHz，其表达式如下：

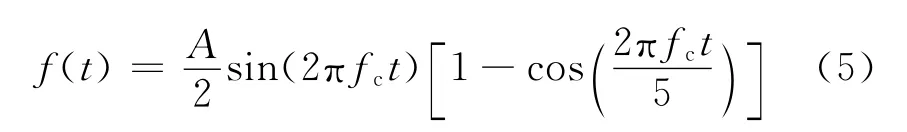
式中A为信号幅值；fc为中心频率。

研究主要关注损伤与S0模态间的相互作用。为了去除边界造成的复杂影响，首先基于无损伤模型对S0模态在铝板中的传播过程进行仿真。随后在无损伤模型基础上，将以D为中心的6.35mm范围内的单元去除，建立损伤模型，基于损伤模型再次对S0模态的传播行为进行仿真。两次仿真结果之差即为单纯由损伤引起的波场变化。

2.3 模拟结果分析

基于上述方法，获得的S0模态传播波场如图4所示。

图4（a）是S0模态在无损伤板中的传播过程，分别显示了37.6，45.7，51.8和58.0μs时整个波场的位移云图。从中可以看出，S0模态逐渐向四周传播，并且位移场强度逐渐减弱。当S0模态到达边界时，将在边界处发生边界反射，形成边界反射波S边界。

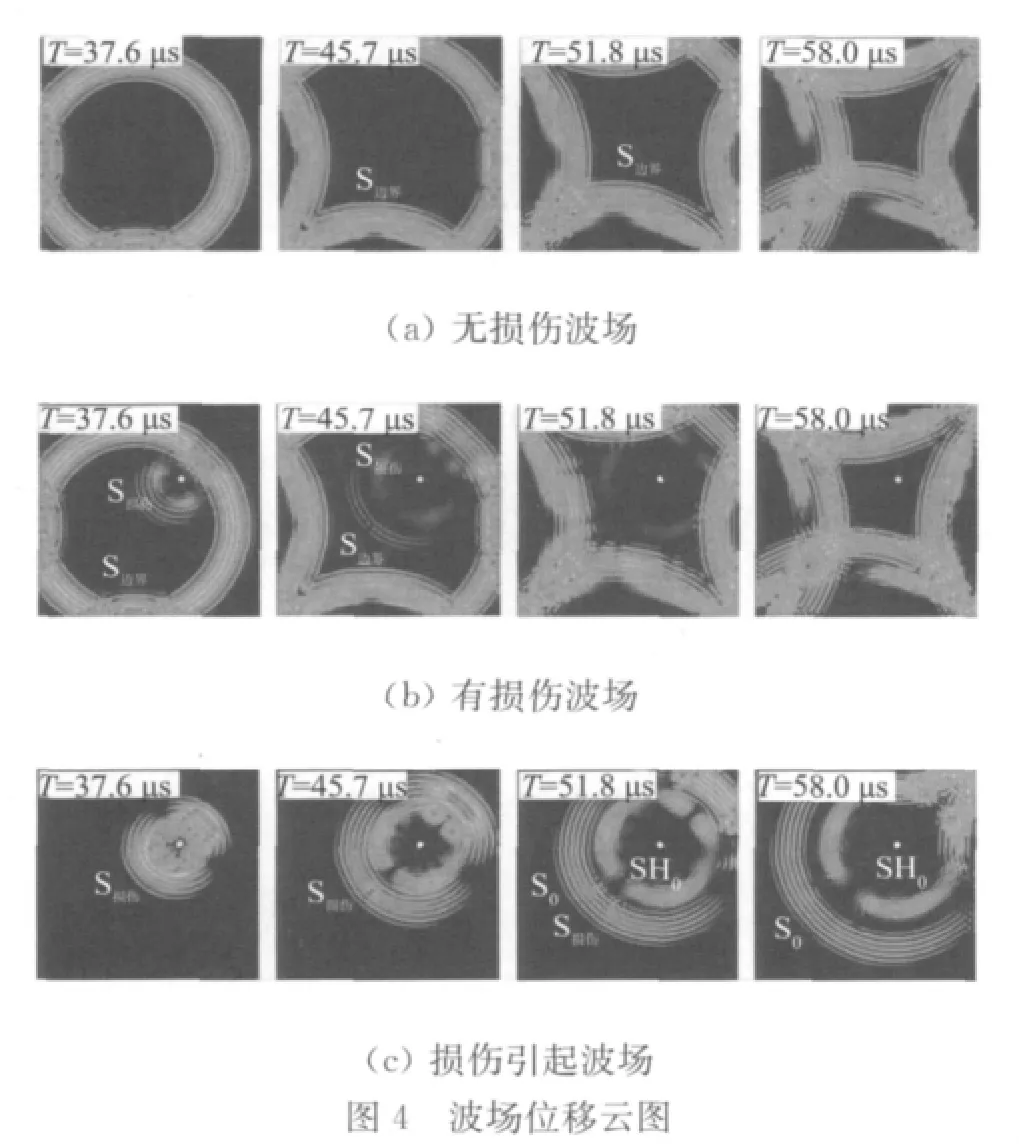
图4（b）显示了S0模态在有损伤板中的传播过程。当S0模态经过损伤时，将发生反射及透射，形成以损伤为中心、向四周传播的位移场，记为S损伤。

为了便于分析损伤对S0模态传播的影响，图4（c）显示了单纯由损伤引起的波场S损伤。从中可以看出，损伤波场以损伤为中心，逐渐向四周扩散。同时，可以观察到S0模态在损伤处反射时，发生模态转换，两种模态由于存在速度差，在传播过程中逐渐分离。为了确定这两个波包所对应的模态，在距离损伤点D140mm处分别提取有损和无损两种情况下的时域信号，两者之差为损伤反射的时域信号，如图5所示。第一个波包包络最大点对应的时间为51.6μs，第二个波包对应的传播时间为68.7μs。

图5 损伤反射信号及包络

根据频散特征方程可知，300kHz下S0和SH0模态波长分别为18.06和10.48mm，传播速度分别为5.39和3.14mm／μs。因此可判断外层波包对应为反射的S0模态，内层波包为S0模态，在损伤处发生模态转换产生了SH0模态。

3 损伤成像

通过上述有限元模型分析可知，S0模态在损伤处会发生透射、反射，形成损伤波场。以下研究基于不同位置接收信号对损伤定位的方法。

3.1 损伤成像算法

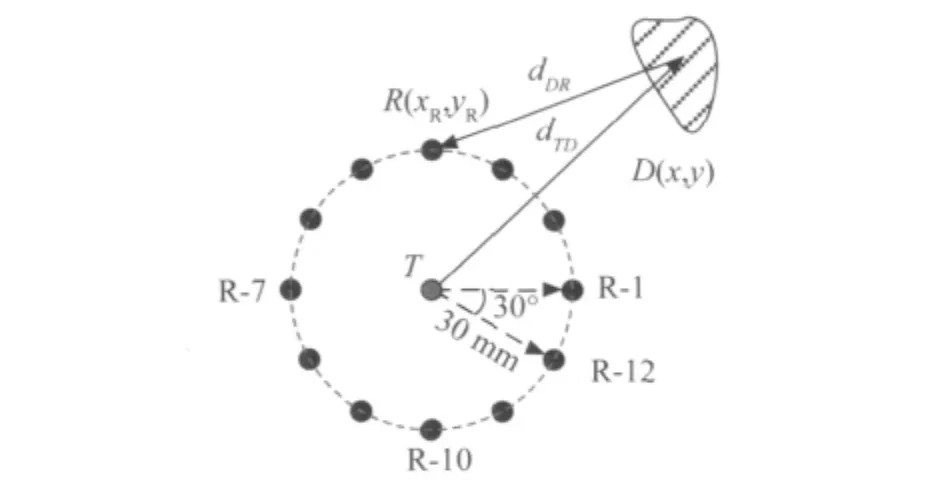
图6 Lamb波传播路径概图

假设板内C点处存在损伤，如图6所示。Lamb波从激发端T到c（x，y），再到接收端R的传播时间为：

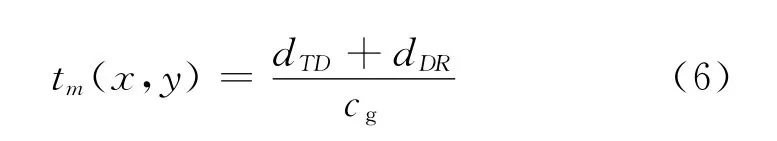
式中cg为导波群速度，dTD和dDR分别是激发点与损伤间和损伤与接收点间距离，分别为：

因此c点反射强度对应在T点激发，在R点接收的损伤信号在tm处能量。时域信号能量通常用其包络表示，信号包络定义为：

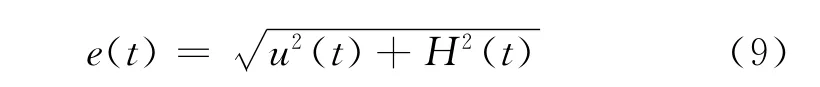
式中 H（t）是信号u（t）的 Hilbert变换；e（t）是信号u（t）的包络。

根据式（6）和（9）可建立平面内任意位置（x，y）处的损伤反射场强值Em（x，y）为：

E（x，y）＝e（t）｜t＝tm（x，y） （10）

损伤图像中各像素点值I（x，y）可使用多对激发－接收组合获得，其计算式为：

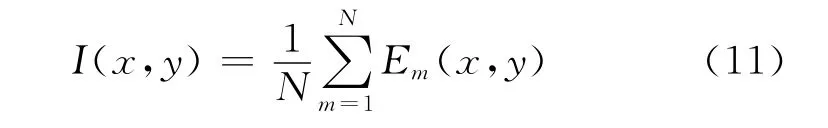
式中N为激发－接收组合数。

3.2 损伤成像

为了获得损伤图像，以激发点T为中心，30mm为半径，30°为间隔，布置12个接收传感器，如图6所示。

根据上述损伤成像算法，利用传感器R－12接收信号可获得单路径损伤分布图像，如图7所示。图中圆圈代表真实损伤位置。从中可以看出，基于单一传感器可以判定多个损伤可能位置，无法对损伤定位。

图8为12个传感器获得的损伤图像叠加，从中可以看出，多路径损伤图像可以指示出损伤位置。在此基础上，对图8引入75%阈值限定，可更加清晰地显示损伤位置，如图9所示。

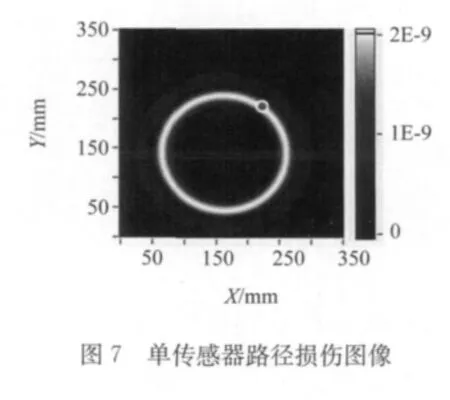
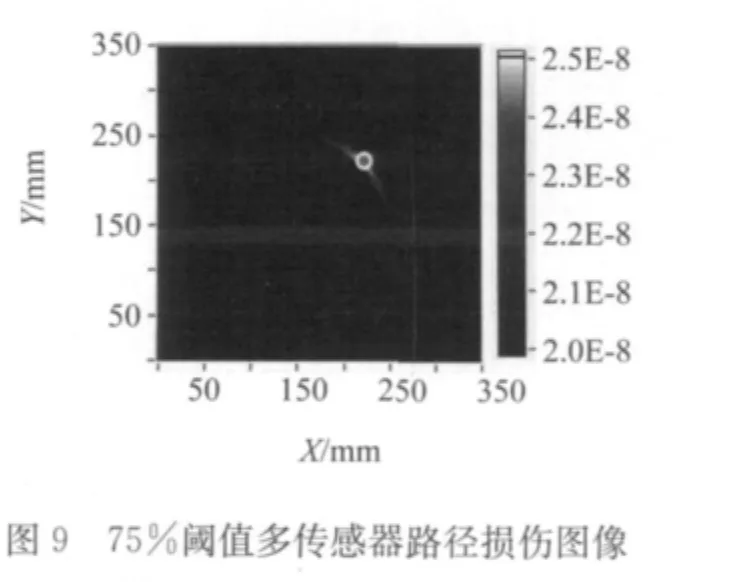
通过上述损伤成像过程可知，仅基于一对激发－接收传感器组合时，损伤图像呈单圆环，无法指示损伤位置。当激发－接收传感器组合增加时，不同的圆环相互叠加，在实际损伤位置，图像强度叠加增强。通过限定最低阈值的方法可以清晰地显示出损伤位置。

4 结论

Lamb波对称模态S0具有传播速度快、低频散的特点，并且以面内位移为主，是损伤检测常用的导波模态。基于有限元方法，对S0模态在铝板中的传播过程进行了仿真研究，并分析了圆孔损伤对其传播的影响。结果表明，在圆孔处S0模态会发生反射、透射，形成损伤波场，并同时伴随有模态转换现象。损伤波场以损伤为中心，向四周传播，同时出现SH0模态。两导波模态传播速度不同，在传播过程中逐步分离。

为了定位损伤，在激发传感器四周建立了环形接收阵列，并基于损伤成像算法获得损伤图像。研究表明，仅基于单一传感器路径，损伤图像呈圆环形，无法定位损伤。基于传感器阵列，损伤图像可以准确指示损伤位置。

然而，当板状结构中存在裂纹且不断扩展时，Lamb波场的变化将更为复杂。裂纹对Lamb波的传播的影响，裂纹扩展与波场变化之间的关系，有待下一步的研究。

［1］武新军，徐江，沈功田.非接触式磁致伸缩导波管道无损检测系统的研制［J］.无损检测，2010，32（3）：166－70.

［2］徐鸿，王冰，姜秀娟.超声导波用于管道缺陷检测的数值研究［J］.动力工程，2009，29（11）：1018.

［3］王强，袁慎芳.复合材料板脱层损伤的时间反转成像监测［J］.复合材料学报，2009，26（3）：99－104.

［4］刘增华，张易农，张慧昕，等.基于磁致伸缩效应在钢绞线中激励接收纵向导波模态的试验研究［J］.机械工程学报，2010，46（6）：71.

［5］徐鸿，李鸿源，王冰.管道中具有累积效应的二阶谐纵向导波生成点的数值验证［J］.固体力学学报，2011，32（1）：82－7.

［6］Cawley P，Lowe M J S，Alleyne D N，et al.Practical long range guided wave testing：applications to pipes and rail［J］.Materials Evaluation，2003，61（1）：66－74.

［7］Rose J L，Avioli M J，Mudge P，et al.Guided wave inspection potential of defects in rail［J］.NDT ＆E International，2004，37（2）：153－61.

［8］Wang C H，Rose J T，Chang F K.A synthetic timereversal imaging method for structural health monitoring［J］.Smart Mater Struct，2004，13（2）：415.

［9］Yu L，Giurgiutiu V.In situ 2－D piezoelectric wafer active sensors arrays for guided wave damage detection［J］.Ultrasonics，2008，48（2）：117.

［10］Su Z Q，Wang X M，Cheng L，et al.On selection of data fusion schemes for structural damage evaluation［J］.Struct Health Monit，2009，8（3）：223.

［11］Rose J，Nagy P.Ultrasonic waves in solid media［J］.The Journal of the Acoustical Society of America，2000（107）：1807.

［12］Yang C H，Ye L，Su Z Q，et al.Some aspects of numerical simulation for Lamb wave propagation in composite laminates［J］.Compos Struct，2006，75（1）：267.