机车轮辋超声探伤信号的数字处理技术

赵 阳，梅劲松，石峥映，屈 蔷

（1.南京航空航天大学 自动化学院，南京 210016；2.南京拓控信息科技有限公司，南京 210042）

超声信号数字处理技术是无损检测领域的重要研究课题。实际工程中，机车轮辋缺陷形式千变万化，如剥落、裂纹、磨耗等，其产生的位置各不相同，且噪声的种类与复杂程度也各异。机车轮辋超声探伤信号的数字处理主要包括两个方面：其一，在多种不确定因素和复杂随机信号的干扰下，将信号处理手段应用于工程实践中，消除噪声并提取有效信号，使得系统具有较强的抗干扰能力。其二，利用去噪后的信号，提取回波信号的数字包络，根据检波包络线，判断机车轮辋有无缺陷和缺陷分布定位，便于后期成像显示。

笔者采用有限冲激响应滤波器（FIR）和小波变换两种算法，分别进行数字滤波并对其作对比分析；将去噪后的信号基于三次样条插值法的数字包络提取技术进行检波处理，最终得到了高精度的探伤分析结果。

1 数字滤波对比分析

1.1 噪声说明

超声探伤信号中的噪声主要包括随机噪声和相干噪声。随机噪声包括环境噪声、材料噪声和电子电路噪声等，是由各种随机因素综合而成的，其频带很宽，在探伤过程中随机出现，将有效信号污染甚至湮没［1］。图1是某纵波双晶探头的超声波探伤信号。

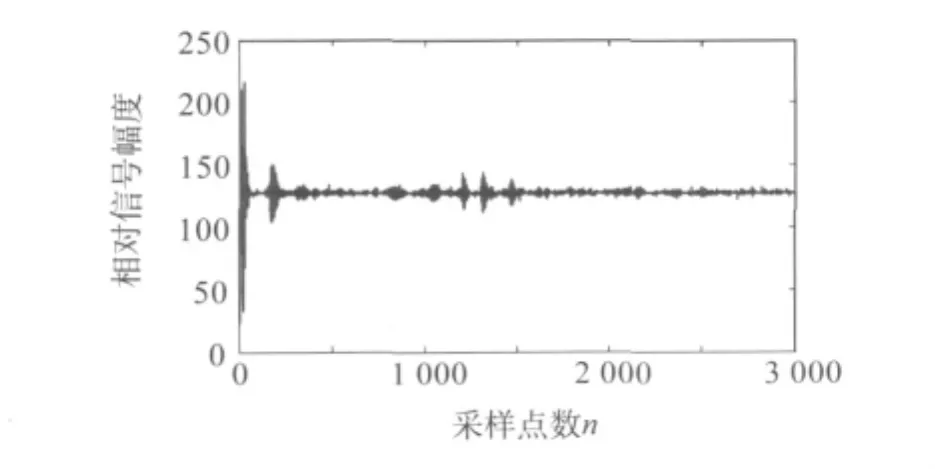
图1 机车轮辋超声探伤的原始信号

图1中的超声波信号是在工业现场采集到的。除了回波脉冲信号外，信号还包括明显的高频噪声，如果将此信号直接用于判伤，会使判伤结果具有很大误差。

1.2 滤波理论及算法

1.2.1 FIR数字滤波器

探伤信号的数字通信要求信号在传输和处理过程中不能有明显的相位失真，使用无限冲激响应滤波器（IIR）是很难做到的。有限冲激响应滤波器（FIR）的系统函数只有零点，除原点外没有极点，所以FIR滤波器总是稳定的，故拟采用FIR数字滤波器［2］。

FIR数字滤波器的基本结构是一个分节的延时线，即把每一节的输出加权累加，得到滤波器的输出。数学上表示为：

式中k为FIR的抽头数；h（i）为滤波器的第i级抽头系数；x（k）为第k时刻的输入样本；y（k）为滤波器的输出样本。其Z域框图如图2所示，其中每个标有z－1的方框代表了一个时钟周期延时的寄存器单元。

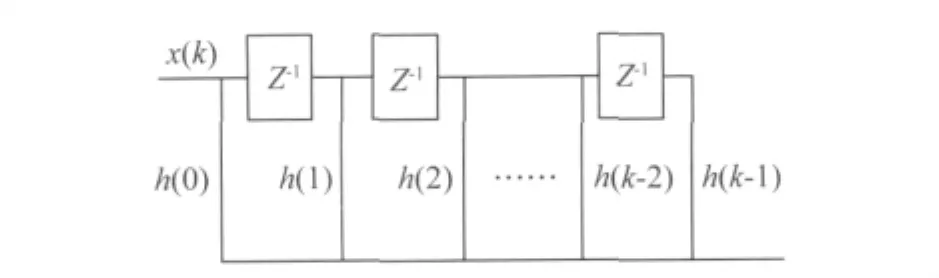
图2 FIR数字滤波器直接实现形式

基于Matlab平台，采用窗函数法设计FIR数字滤波器［3］。窗函数法基本思想是用一个有限长度的窗口函数序列ω（k）来截取一个无限长序列hd（k），获取一个有限长序列h（k）。数学上表示为：

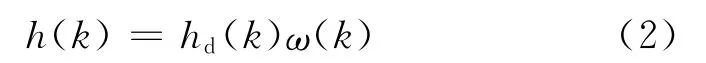
窗函数的设计要满足两个条件：① 窗谱主瓣尽可能地窄，以获得较陡的过渡带。② 尽量减少窗谱的最大旁瓣的相对幅度，即将能量尽量集中于主瓣，使峰肩和纹波减小，就可增多阻带的衰减。

1.2.2 小波变换

FIR数字滤波器是属于经典的去噪方法，它是把有效信号和噪声在频域范围进行分离的方法。这种方法多用于信号频谱和噪声频谱没有重叠的情况下。而小波变换是一种窗口大小固定，窗口的形状可变、时间窗和频率窗都可改变的时频局部化分析方法。该方法在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，很适合用来探测在白噪声等非平稳信号污染下的有效信号中的尖峰成分。

在超声探伤中取如下含噪的一维信号模型：

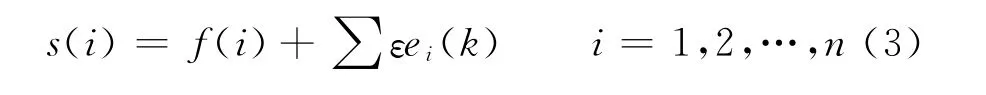
式中s（i）为含噪信号；f（i）为有效信号；∑εei（k）为噪声叠加；ei为独立同分布的高斯白噪声N（0，1）；n为信号长度。取s（i）进行了5层分解，即5层多分辨分析：

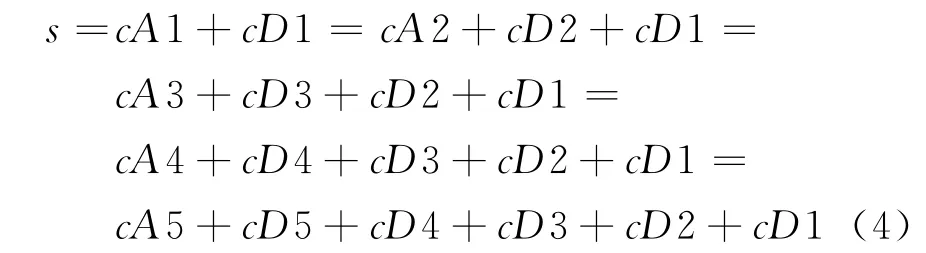
在分解过程中，有效信号通常为低频信号或平稳信号，产生系数为k层尺度空间的尺度系数，而噪声信号通常表现为高频信号，产生系数为k层小波空间的细节系数。上式cAk是各层的尺度系数，cDk是各层的细节系数，k＝1，2，3，4，5。将分解后的小波系数采用门限阈值处理。处理过程中最为重要的就是如何选择阈值和阈值量化函数。常用的阈值原则有4种：固定阈值原则、无偏似然估计原则、极值阈值原则和启发式阈值原则。而最常用的阈值量化函数有两种：硬阈值函数和软阈值函数。若令t表示阈值，t＞0，则硬阈值信号s的形式为：

软阈值信号s的形式为：

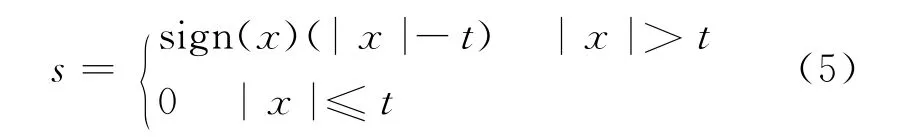
与硬阈值函数相比，软阈值函数具有更好的数学特性，且处理的结果更为平滑。故采用软阈值函数对小波系数量化处理。将阈值量化过后的小波系数作逆变换W－1重构信号，即：

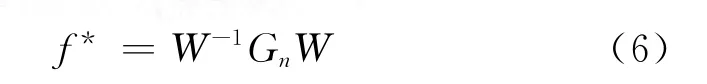
式中GnW 为对小波系数W 作门限阈值处理；f＊为重构后的去噪信号。

1.3 仿真验证

基于图1中的超声探伤信号数据进行试验。纵波双晶探头的中心频率是2.5MHz，采样频率是20MHz，每周期采点数是3000，截止频率是2.4和2.8MHz。

窗函数中能提供＞50dB的最小阻带衰减的是海明窗、布莱克曼窗和凯泽窗三种。但海明窗的旁瓣峰值最小，主瓣宽度最窄，可以使滤波器的阶数较少，所以选用海明窗来设计FIR数字滤波器。

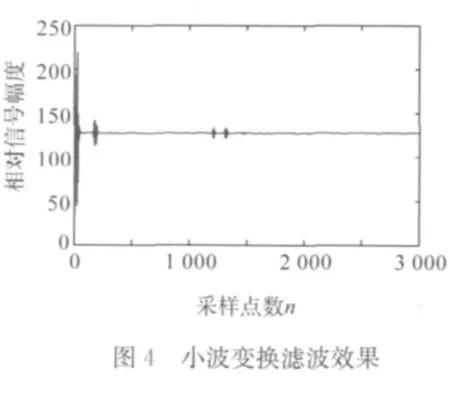
同时运用小波变换进行信号消噪。选择与超声探伤的脉冲信号较匹配的Daubechies小波系［4］中的db4小波基，基于Mallat算法进行5层多分辨分析，阈值化处理后重构信号，析出有效信号。将基于FIR的数字滤波器滤波方法与小波变换的方法进行对比，其对比结果如图3和4所示。

图3中，使用FIR数字滤波器并没有达到理想的去噪效果。因为在探伤实际工程中，所遇到的信号大多数是不平稳的，而非平稳信号的时变特性包含了很多方面，只采用单一的手段和窗函数，必然会产生一些不可避免的误差，可能出现不完整滤波。虽然这严格上不算错误，但无法有效地反映信号本质的局部特征，故达不到理想的去噪效果。

由图3和图4的对比可见，采用同样原始数据的情况下，基于小波变换的消噪方法与FIR数字滤波器相比，在去噪效果上的有效信号辨识度更高、抗干扰能力更强；小波变换滤波后的脉冲信号表现更加光滑、平整；在回波能量损失上，FIR对始波抑制很严重，这种去噪方式是以牺牲清晰度为代价而换取的，故达不到理想的去噪效果。

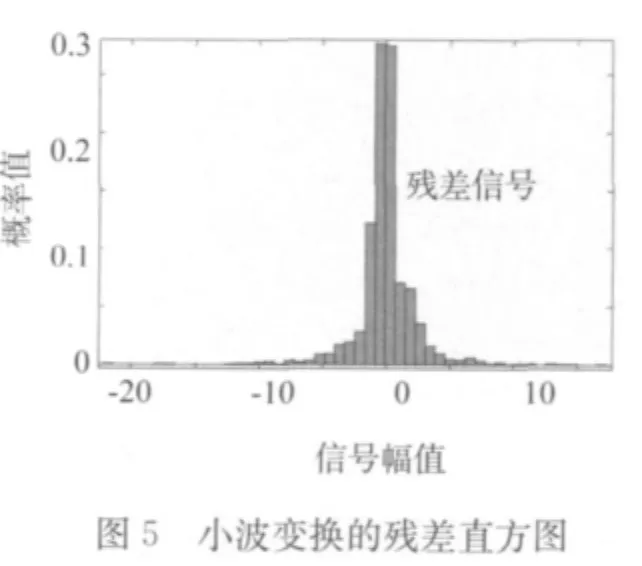
对经小波变换的残差信号作残差分析并得到残差直方图，如图5所示。

残差是指实际观察值与回归估计值的差。它的数据量与相对比的数据个数是相等的。分析图5，直方图符合近似正态分布，且残差信号的概率主要集中在幅度为0的邻域内，可见消噪后的信号与原始信号相差较小，滤波效果较好。

以上超声探伤信号的研究表明：使用小波变换时，高频系数的幅值随着分解层次的增加而迅速地衰减。在此基础上，选用不同的尺度因子对原始信号进行分析，相当于用一系列带通滤波器对信号作不同频段的频谱分析［5］，故小波变换相比于FIR数字滤波器更适合对超声探伤信号消噪。

2 信号包络的检波分析

小波变换虽能滤除超声回波信号的大部分噪声，但是要准确地提取回波，方便技术人员判伤，还需要根据回波信号的包络来进行分析。笔者将经小波变换后的滤波信号采用样条插值法来提取信号包络，以便工程技术人员判伤。

样条法是用一平滑曲线对各主干点进行拟合的方法。它是通过构造不同阶多项式来形成一条把所有主干点连接起来的平滑曲线。一般常常选择三次曲线（根据三次插值样条函数所得的曲线）进行拟合。

数学上寻找插值函数是相当复杂的［6］，但Matlab平台提供了现成的三次样条插值函数，既简化了源程序编写难度，又利用其强大的作图功能方便地拟合出光滑曲线，为工程应用提供了便利。

将小波变换后的去噪信号作为输入信号，基于Matlab抽取信号上以5个点为区间的局部极大值点作为各主干点，结合三次样条插值法对曲线拟合，提取图4信号的正包络线如图6和7所示。

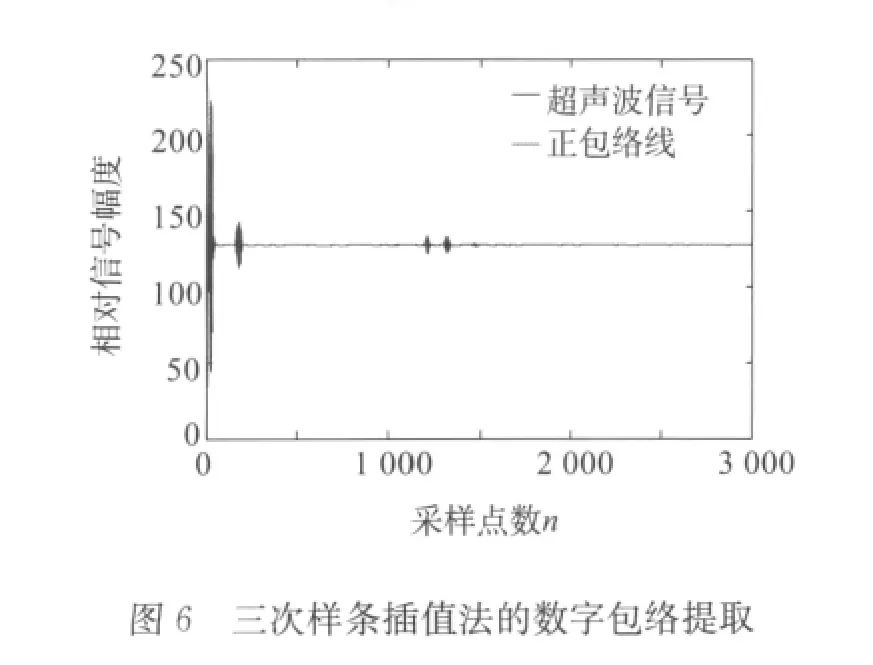
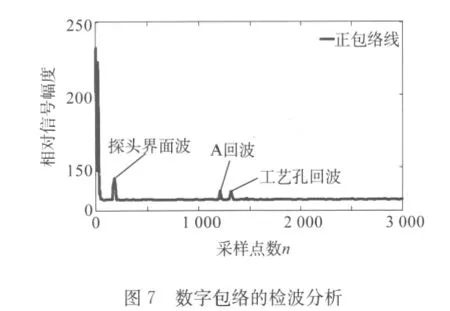
在图6，7的正检波分析中，探头界面波与探头特性和工艺相关，因探头而异，可以理解为始波范畴；工艺孔回波是由于超声波遇到机车整体轮中的应力孔而反射回来的回波信号，其峰值在点n1＝1313处，根据超声波在机车轮辋中的声速v＝5920m／s，可以计算出s1＝194.324mm，与应力孔位置相符；A回波产生的可能性比较复杂，主要有两种原因：缺陷存在或应力孔周围不平整，其峰值在点n2＝1206处，根据超声波在机车轮辋中的声速v＝5920m／s，其位置在s2＝178.488mm处。不管哪种可能，均已经较好地表明文中的数字检测方法是有效的。

3 结语

对FIR数字滤波器和小波变换的去噪能力作了对比分析。在分析小波去噪后的信号时，提出了三次样条插值法提取超声探伤信号的数字包络，构建了以数字滤波和包络检波为核心的超声探伤信号的数字处理技术。研究表明，鉴于超声探伤信号中的噪声具有非平稳性和复杂性的特点，传统的滤波器已不如小波变换更加适用；选取能够得到平滑曲线、具有优良数学特征的三次样条插值法来提取探伤信号的数字包络曲线是合适的。文中的数字处理技术可用于超声探伤信号分析，具有辨识度高和抗干扰能力强的特点，在实际工程中具有广泛的应用前景。

［1］胡天明.超声探伤［M］.武汉：武汉测绘大学出版社，1996.

［2］何晓丽.高速磁浮列车间隙检测信号的数字滤波器设计与实现［D］.成都：西南交通大学，2008.

［3］陈亚勇.MATLAB信号处理详解［M］.北京：人民邮电出版社，2001：163－167.

［4］张广明.超声无损检测中的时频分析理论及应用研究［D］.西安：西安交通大学，1999.

［5］邹晓红.小波分析在超声回波测量中的应用［J］.传感器技术，2005，24（7）：78－82.

［6］鞠时光，郭伟刚.实用三次样条插值函数［J］.小型微型计算机系统，1992，13（9）：20－23.