基于未确知测度的人才综合测评模型

薛俊锋，李 莉，赵子月，夏自强

(1.邯郸市邯三建筑工程有限公司，河北邯郸056001;2.河北工程大学土木工程学院，河北邯郸056038;3.新兴铸管股份有限公司，河北邯郸056300)

传统的人才测评技术大都是定性分析［1]，其专家系统实际上是一个二值结构的逻辑系统［2]，只在“是”与“非”之间取值，定量化研究比较少。在实际的人才测评中，经常遇到模糊或不确定的语意，无法仅仅采用“是”与“非”进行定量描述，而模糊综合评判［3－7]适用于这种情况下的人才测评。但是，在模糊综合评判中，作为隶属度的可信度并没有把测量准则作为必要的限制条件。因而，作为测量结果的隶属度并不是测量意义上的某种测度，并且在合成可信度的推理算法上存在缺陷。

本文把定性分析与定量描述相结合，建立了基于未确知测度和指标分类权重的人才测评模型，修正了模糊综合评判模型中的不足。在此模型中，隶属度是严格测量意义上的某种可能性测度;在合成可信度的推理算法中，定义了对分类贡献大小的指标分类权重的概念，给出了指标分类权重的计算方法，并把它用于合成可信度的计算中。

1 未确知测度模型

设x1，x2，…，xn表示 n 个待测评人员，X={x1，x2，…，xn}称为论域;评价 xi(1≤i≤n)有 m 项指标 I1，I2，…，Im，称 I={I1，I2，…，Im}为指标空间，测评指标可以是定量指标，更多的是定性指标;定量指标必须是可以测量的，定性指标必须定量化。用xij表示对象xi在指标Ij下的观测值。C为评语空间 c1，c2，…，ck，是 C 的一种划分，即)其中，ck(1≤k≤K)为第 k个评语等级［8]。

1.1 单项指标下的未确知测度

对象xi关于指标Ij的观测值为xij，即xi处于第k(1≤k≤K)个评语等级的程度用［0，1] 上的实数具体表示，这个实数记为 μijk=μ(xij∈ck)，(1≤i≤n，1≤j≤m任意固定，k在1与K之间取值)。符号“xij∈ck”表示观测值 xij使对象 xi处于状态 ck，并非通常意义下元素与集合间的含义。μijk是对“程度”的测量结果，是一种可能性测度，作为一种测量结果的这种可能性测度它必须满足通常的诸如“非负有界性、可加性、归一性”三条测量准则［9]，即:

(1)非负有界性:0≤μ(xij∈Ak)≤1 (1≤i≤任意固定;Ak为C的任意子集)。

(2)可加性:μ(xij∈∪Ak)=

(3)归一性:μ(xij∈C)=1。

称满足上述三条测量准则的μ为未确知测度，简称测度。μijk为对象 xi的单指标测度评价矩阵。

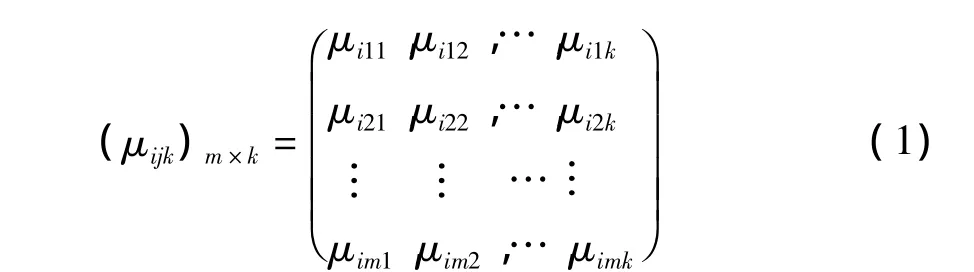
(i=1，2，…，n j=1，2，…，m k=1，2，…，k)

其中，μijk= μ(xij∈ck)(1≤i≤n，1≤j≤m，1≤k≤K)表示观测值xij使xi处于ck评语等级的未确知测度。

1.2 指标分类权重

设使对象xi关于指标Ij的观测值xij处于c1，c2…，ck各个评语等级的未确知测度向量为

ij1ij2ijkjxi处于各个评语等级的程度相同，因而无法区分出xi到底处于哪个评语等级。此时称指标Ij对xi的分类未做出贡献，记=0。

2)如果K个μijk中有一个μijk0=1，其余的K－1个均为0，则指标Ij使xi确定地处于评语等级，称指标Ij对xi的分类做了最大贡献，则这时应取到最大值。

指标Ij对xi的分类贡献的大小可以由指标分类权重定量描述，而大小由的各个分量取值的集中与分散程度描述，而各分量取值集中与分散的程度有多种描述方法，最典型的一种是信息熵。由测度μijk所确定的信息熵［10]为

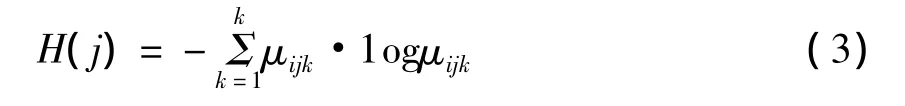
令

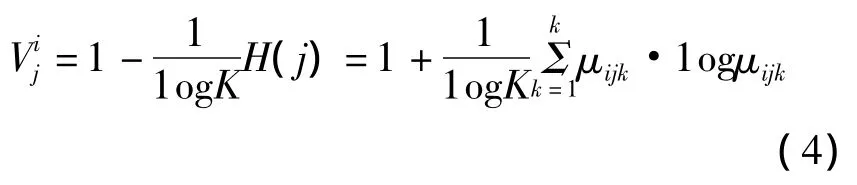
由信息熵的性质知:

2)当且仅当存在一个μijk0=1其余的K－1个均为0时，Vj取到最大值为1。

3)μijk取值越集中，Vj的值越近于1，反之 μijk取值越分散时，Vj的值越近于0。

令

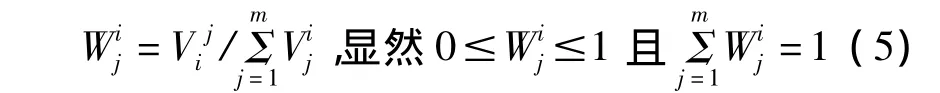
由Vj的上述三条性质可知，由(5)式定义的wj

i正是我们感兴趣的指标Ij关于xi的分类权重。

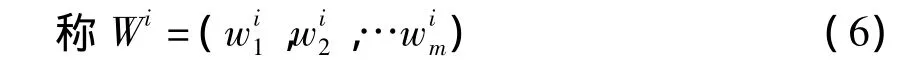
为指标I1，I2，…，Im关于xi的分类权重向量。指标Ij关于xi的分类权重是由矩阵(1)中的第 j行(μij1，μij2，…，μijk)中测度值计算得到的，或说是由Ij指标(值)提供的分类信息经计算求出来的，既然可以算出来，说明它不可能由专家主观拟定。

1.3 综合评价系统

若关于xi的单指标测度评价矩阵(1)已知，关于xi的各指标分类权重向量为式(6)。

令

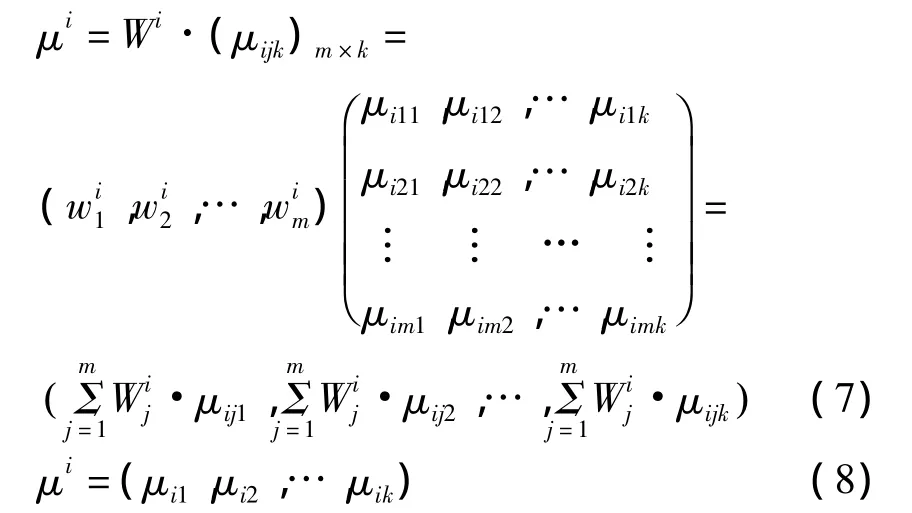
则μi为xi的评价向量。其中μijk(1≤k≤K)表示xi处于ck等级的未确知测度。式(8)具体描述了xi的不确定性分类，为了输出确定性分类结果，需进行识别。

1.4 识别准则

因评语等级划分是有序的，比如，第k个评语等级ck“好于”第k+1个评语等级ck+1，这种情况下最大测度识别准则不适用，改用置信度识别准则。

设置信度为 λ，(λ ＞0.5)通常取作 0.6或0.7，令

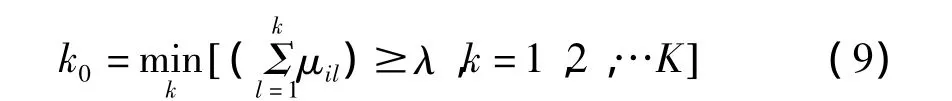
则判xi属于第k0个评价等级ck0。真实含意是xi不低于ck0等级的置信度为λ，或说低于ck0等级的置信度是1－λ。

2 综合评价算例

根据上述未确知测度评价模型，以邯郸市邯三建筑有限公司的20名中层以上核心职工为例进行测评。参评的专家及领导10人，分别在品德素质、智力素质、绩效评价、身体评价和能力素质五个方面，共30个评价指标进行评测。评价指标体系如表1所示。评语空间为{优，良，中，一般，差}。

测评方式:采用专家打分，关键是确定合理的打分规则。在这30项指标中，规定每项指标以10分计，分布于5个评语等级上。不同的等级分使待评对象处于不同的测评等级。这种打分规则避开了指标重要性权重;另一种规则是:每项指标满分10分，每个待评对象在0～10间得到一个分值;再用指标重要性权重乘以得分，并按总分进行分类。但这要求估计指标重要性权重。每个待评对象均得10分，区别在于每个待评对象的等级分不同。这样的打分原则是公正的，也符合“非负有界性、可加性、归一性”的测量准则。10名专家对20名职工按上述原则逐一“打分”，统计打分结果，取平均值并作整数化处理得到，待评对象1的得分如表2所示。

表1 指标体系结构Tab.1 Index system structure

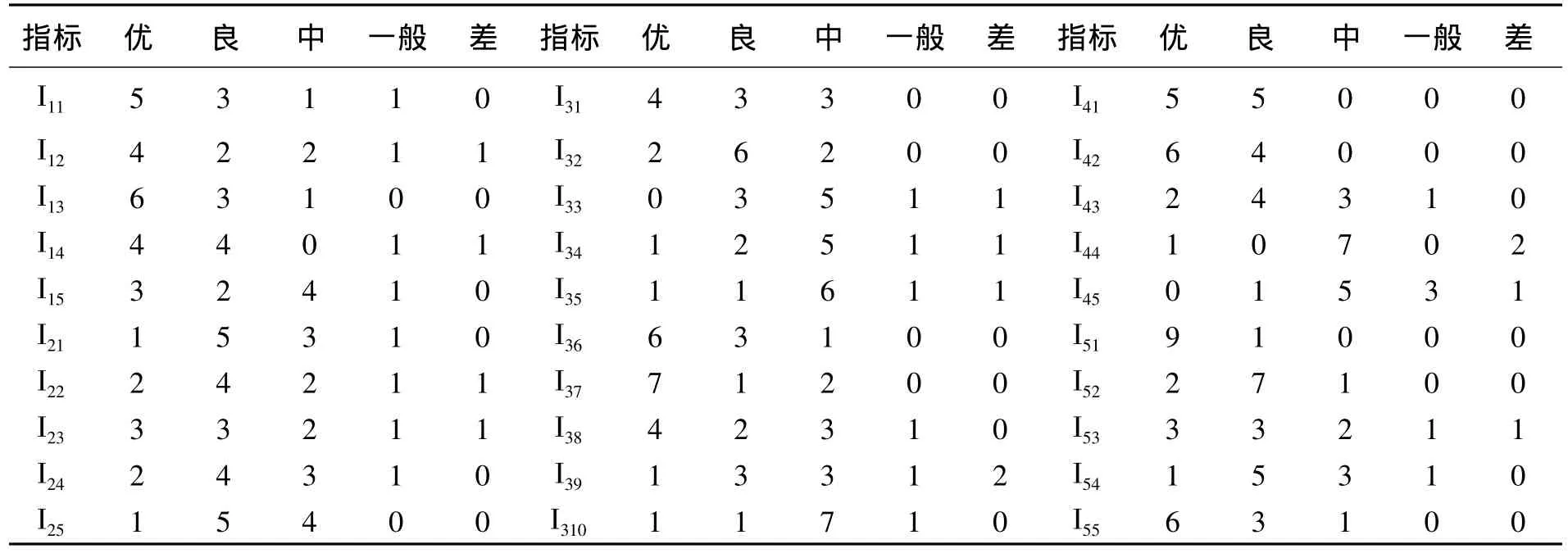
表2 对象1的测评统计得分表Tab.2 Assessment statistical scoring sheets of object 1

根据表2的统计数据得到如下单指标测度矩阵:

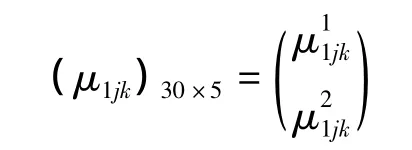
其中

根据式(3)－式(6)计算指标分类权重，关于对象1的各指标分类权重向量为

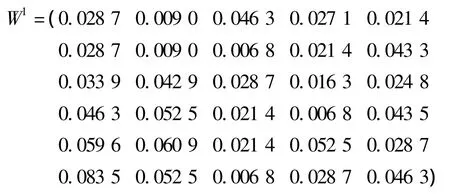
由上式计算对象1的评价向量为

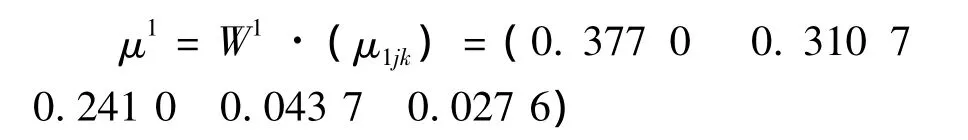
取 λ =0.6 有:当 k0=2 时，0.37 70+0.310 7+0.687 7 ＞0.6= λ

因此，对象1被评价为良，同理可对其余待评对象进行测评。此测评结果相对合理，领导及专家比较满意。

3 与模糊综合评判模型的区别

人才测评方法虽很多，各有优点和不足。最为典型的方法是模糊综合评判模型。本文方法与模糊综合评判的主要不同在于:(1)本文方法要求每个测评对象的单指标测度必须满足关于测量的三条准则。对于人才测评，各单指标测度是由专家“打分”的方法得出，那么打分应体现“公正”原则:每个测评对象在每项指标上均得10分，这10分分布在不同的测评等级上。这就是公平性原则，由此得到的单指标测度显然满足关于测量的三条准则。(2)合成测度是各单指标测度的加权平均，而“权”是各指标的分类权重，而指标的分类权重是由对象关于指标的观测值提供的分类信息计算求得的，它的语意是该指标对对象分类做出贡献的大小。这一点是本文方法与模糊综合评判合成可信度中最本质的区别;在模糊测评合成可信度中用的是指标的重要性权重，指标重要性权重是由专家主观拟定的。事实上，专家主观拟定的指标重要性权重与观测值无关，它对所有待评对象具有通用性，因为没有对特定的待评对象提供针对性的分类信息，因而不能用于特定对象分类。

4 结语

应用本文模型的测评结果由矩阵(1)完全确定，除此之外，不再需要任何先验信息。本文确定的打分规则:每个待评对象在每项指标上均得10分，区别在于不同评语等级上的得分不同，从测量角度讲是合理的。

［1] 梁建.人事测评技术及其理论发展［J] .外国经济与管理，2000，22(7):19－23.

［2] 张德新，崔 巍，艾庆生.人才素质的模糊评价［J] .电脑与信息技术，2010(5):8－9.

［3] 高勇强.人事考核的多层次模糊综合评判法［J] .中国管理科学，2010，8(2):44－49.

［4] 梁 镇，刘 岩.我国人才测评技术发展现状分析［J] .商业研究，2002，38(1):35－37.

［5] 牛丽文，夏冬艳，任丽媛.基于未确知测度的企业业绩评价模型研究［J] .河北建筑科技学院学报，2006，26(3):91－94.

［6] 李万庆，张立宁，孟文清.基于信息熵与未确知测度的MIS综合评价模型研究［J] .河北建筑科技学院学报，2005，22(3):49－53.

［7] 王晓波.基于未确知测度理论的CCPM缓冲区尺寸设计［J] .河北工程大学学报:自然科学版 ，2011，28(1):76－80.

［8] 曹庆奎，李琴，于兵.基于未确知测度的高新区技术创新环境评价［J] .科技进步与对策，2009，26(9):124－127.

［9] 曹庆奎，李建光，杨艳丽.基于信息熵和灰关联分析的煤矿企业供应商评价选择研究［J] .河北工程大学学报:自然科学版，2008，25(1):81－84.

［10] 吴茂森.概率与信息［M] .上海:科学技术出版社，1960.