鱼雷捷联惯性系统尺寸效应引起的误差分析＊

孙 权

（海军驻昆明七五〇试验场军事代表室 昆明 650051）

1 引言

由于采用了高速、大容量的数字计算机和一些新技术，捷联式惯性导航系统具有精度高、反应时间短、可靠性高、体积小、重量轻、成本低、维护方便等优点。目前捷联技术已广泛应用于飞机、舰船、导弹上。在鱼雷上应用捷联惯性技术可以有效解决鱼雷精确制导问题，并实现复杂弹道，它是提高鱼雷技术性能和实现鱼雷智能化的重要手段。

鱼雷捷联惯性系统用直接安装在雷体上的加速度计和陀螺仪来测量沿雷体坐标轴的鱼雷相对于惯性空间运动的加速度和角速度分量，在导航计算机中进行实时解算，从而求得鱼雷航行控制所需的航向、姿态角等导航控制参数。加速度计和陀螺仪安装于惯性测量装置（IMU）底座上以及IMU安装于鱼雷上，都不可避免地会产生安装误差，此误差包括两个方面内容：

1）加速度计和陀螺仪的测量输入轴同鱼雷坐标轴线不一致引起的安装误差；

2）惯性测量组件中的加速度计偏离鱼雷摇摆中心引起的安装位置误差。

惯性测量组件中的加速度计理想定位应在鱼雷的质心，但实际上是不可能的。当加速度计偏离该理想位置和鱼雷作旋回运动、蛇形运动或摇摆运动时，由于存在离心加速度和切向加速度，故会引起加速度计的测量误差，这种现象就是尺寸效应，尺寸效应最终引起鱼雷导航控制参数误差。本文只分析安装位置误差引起的尺寸效应对系统导航性能的影响。

2 尺寸效应分析

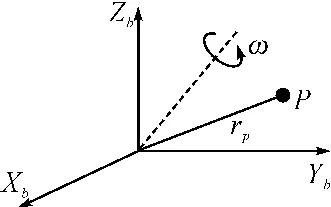
图1 尺寸效应示意图

设加速度计偏离鱼雷质心距离为rP，见图1，图中b系为雷体坐标系，雷体坐标系是固连在鱼雷雷体上的坐标系，雷体坐标系的坐标原点O位于雷体的重心处，OXb沿雷体横向指向右，OYb沿雷体纵轴指向前，OZb垂直于OXbYb并沿雷体的竖轴指向上。当雷体坐标系相对惯性坐标系i（惯性坐标系的原点为地球地心Oe，三个轴均指向惯性空间的的某一个方向不变，惯性坐标系是惯性敏感元件测量的基准）以角速度ω作旋转运动时，由于向心加速度以及切向加速度的影响，加速度计必然产生误差，其大小为

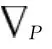
3 鱼雷捷联惯性系统误差方程

3.1 数学平台误差方程

在鱼雷捷联惯性系统中，数学平台应模拟导航坐标系，这里导航坐标系取为地理坐标系t，地理坐标系是在雷体上用来表示鱼雷所在位置的东向、北向和垂线方向的坐标系。地理坐标系的原点O选在雷体重心处，OXt指向东，OYt指向北，OXt沿垂线方向指向天。数学平台为模拟地理坐标系计算出的地理坐标系称为计算地理坐标系（记为t′系），由于数学平台因各种误差源存在误差，故计算地理坐标系t′和真实地理坐标系t之间存在误差角，称为失准角。设φx、φy、φz分别为t′与t之间的东向、北向、方位失准角，鱼雷在地理系中三个坐标轴上的速度分量分别为Vx，Vy，Vz，鱼雷所处位置为经度λ、纬度L，则鱼雷捷联惯性系统的数学平台误差方程可用以下公式表示［2］：

3.2 鱼雷速度误差方程

鱼雷捷联惯性系统的速度误差方程为［2］

3.3 位置误差方程

鱼雷捷联惯性系统的位置误差方程为［2］

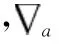
4 尺寸效应引起的系统误差仿真

为了简化分析加速度计尺寸效应对系统导航性能的影响，以鱼雷作旋回运动为例，对鱼雷捷联惯性系统尺寸效应引起的系统误差进行仿真。

4.1 加速度计误差的计算

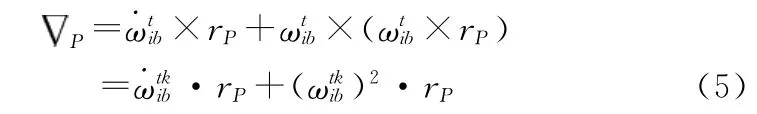
式中ψ，θ，y分别为鱼雷的航向角、俯仰角、横滚角。

图2 鱼雷旋回运动示意图

鱼雷在水平面内作匀速旋回运动示意图见图2。

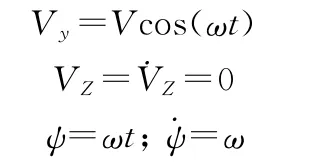
设

另外：

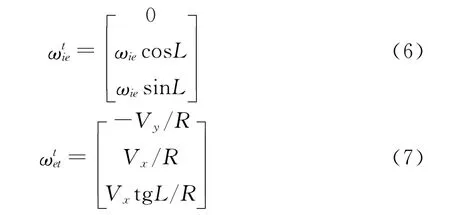
故：

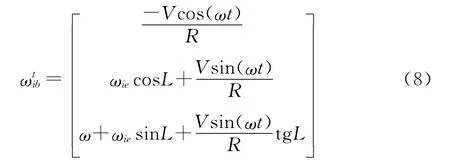
由于鱼雷作旋回运动，速度又较低，可以认为L基本不变，所以有：

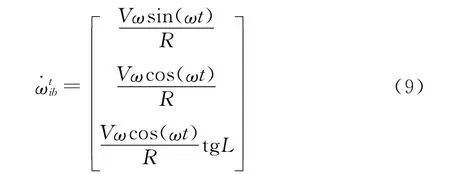
4.2 误差仿真

为了分析尺寸效应对系统导航性能的影响，在鱼雷捷联系统误差方程中，不考虑系统其它误差源，即认为加速度计本身的零偏、陀螺漂移为零，只把尺寸效应引起的加速度计误差作为误差源。设鱼雷在水平面内作匀速旋回运动，其运动参数如下：

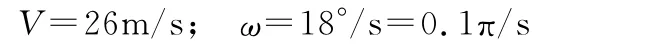
在平台误差方程、速度误差方程和位置误差方程中不考虑垂直通道Z 向分量，把Vx＝26sin（ωt），Vy＝26cos（ωt），L＝35°，fx＝Vωcos（ωt），fy＝－Vωsin（ωt），fz＝g代入即可得到鱼雷作旋回运动情况下尺寸效应引起的误差方程，并设加速度计偏离鱼雷质心距离rP为

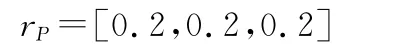
初始误差为

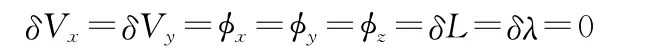
根据误差方程编写程序进行仿真。仿真时间为200s的系统误差曲线见图3，仿真时间为3h的系统误差曲线见图4。

图3 尺寸效应引起的系统误差（200s）

图4 尺寸效应引起的系统误差（3h）

5 结语

由仿真结果可知，加速度计尺寸效应将引起系统误差。刚开始随着时间增长，系统的积累误差越来越大；再以后系统各项误差均出现了振荡，除速度误差δVx，δVy外，其余各项误差都产生了常值误差。加速度计尺寸效应对速度误差影响最大，δVx，δVy一开始便呈直线增长趋势，当t为100s时，速度误差就达到了2m／s，而鱼雷速度本身才为26m／s；对于所引起的数学平台误差，200s以内其值是比较小的，为角秒级，半小时以内最大也不过10角分左右，而实际上鱼雷作旋回运动一般是不会超过半小时；对于经纬度误差，当仿真时间小于100s时，其值不是很大，为10－4数量级，但在这以后，经纬度误差就逐渐很大了。

以上仿真是在鱼雷速度为26m／s，旋回角速度为18°／s，加速度计偏离鱼雷质心距离rP为［0.2，0.2，0.2］的情况下得出的结论。若鱼雷速度、旋回角速度较低，rP较小，则加速度计尺寸效应引起的系统误差比目前要小许多，基本可以忽略。

［1］张树侠，孙静.捷联式惯性导航系统［M］.北京：国防工业出版社，1992：154－157.

［2］以光衢.惯性导航原理［M］.北京：航空工业出版社，1987：48－61.

［3］袁信，俞济祥，陈哲.导航系统［M］.北京：航空工业出版社，1993.

［4］戴自立.现代舰艇作战系统［M］.北京：国防工业出版社，1998.

［5］袁信，俞济祥，陈哲.导航系统［M］.北京：航空工业出版社，1993.

［6］周徐昌，黄文玲，等.鱼雷控制系统设计［M］.武汉：海军工程学院，1995.

［7］郭齐胜，董志明，单家元.系统仿真［M］.北京：国防工业出版社，2006.

［8］罗家洪，方卫东.矩阵分析引论［M］.广州：华南理工大学出版社，2006.

［9］周建新.MATLAB从入门到精通［M］.北京：人民邮电出版社，2008.

［10］曹小平，汪百年.捷联惯性系统的误差及其特性分析［J］.光电与控制，2004（3）：54－56.