大跨度预应力混凝土连续刚构桥自振特性分析

许力沱，王海良，常春伟

（1.天津城市建设学院 土木工程系，天津 300384；2.解放军军事交通学院 军事交通系，天津 300161）

桥梁抗震性能的研究离不开对结构自振特性的分析，结构自振特性是其动力特性分析的重要参数，是结构本身所固有的，反映了桥梁的刚度指标.了解结构的自振特性是进行进一步地震反应分析的前提.目前，对大跨度混凝土连续刚构桥的自振特性影响因素的研究多集中在混凝土弹性模量、主梁自重等上部结构因素变化对其的影响[1]，而对桥墩高差和上部结构边中跨比对结构自振特性的影响研究较少，为了查明桥墩高差和上部结构边中跨比变化对其自振特性的影响程度，本文以大准铁路增二线内蒙古黄河特大桥主桥为对象，分析了其自振特性的一般性规律，并研究了不同的桥墩高差和边中跨比对结构自振特性的影响，对此类桥梁在今后的抗震设计、抗风稳定性分析和健康检测和维护等方面都具有重要意义.

1 工程概况及有限元建模

大准铁路增二线内蒙古黄河大桥主跨结构形式为 96m+132m+96m大跨度预应力混凝土连续刚构，采用单箱单室截面箱梁结构，支点处梁高9.2m，跨中和边跨端部梁高5.0m，梁体下缘除中支点处12m、中跨中部10 m和边跨端部35.7 m梁段为等高段外，其余均按二次抛物线变化.箱梁顶板宽8.1m，底板宽6.1m，除梁端附近区段外顶板厚为0.5m，底板厚度从0.4m按二次抛物线变化至0.9m，腹板厚度从0.45m按折线变化至0.9m，梁体在支点及中跨跨中共设置7道横隔板，端部横隔板厚1.5m，刚臂墩处横隔板厚度1.2 m，中跨跨中横隔板厚1.0 m.刚臂墩采用混凝土矩形空心墩，纵向宽度6 m，壁厚1.2m，横向采用变宽设计，顶宽7.3m，壁厚1.05m，外坡按20∶1变化，内坡按80∶1变化，1号墩高49.7m，2号墩高47.7m.桥梁总体布置图见图1，连续刚构桥横截面图见图2.

运用M idas/civil 2010软件建立模型，模型由154个节点、147个单元、66个截面组成，主梁左右两端为双支座，施加横桥向、竖向位移约束Dy、Dz，以及绕顺桥向转动约束Rx，释放其他自由度，桥墩与主梁固结，并考虑主梁梁高因素，将桥墩墩顶单元的节点与相对应主梁节点设置主从约束（固结），坐标采用全局坐标系（右手法则X、Y、Z轴垂直坐标系），有限元计算模型见图3.

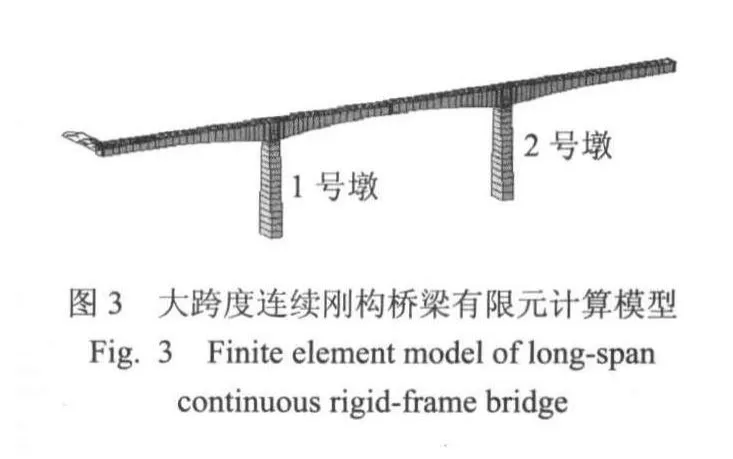
2 自振特性的计算结果

求解结构的自振频率或者周期实质上是求解一个广义特征值的问题.求解特征值问题的方法很多，如逆迭代法、瑞利—里兹法、里兹向量法、子空间迭代法、lanczos向量法.目前常采用子空间迭代法来计算，子空间迭代法是求解大型矩阵特征值问题最有效而常用的一种方法，它适合用来求解部分特征解的问题.它的方法是：在保持正交条件下，假设个起始向量，同时进行反复的迭代，当迭代次数足够大到满足收敛条件时，则可得矩阵的前个特征值及特征向量.故本文选用子空间迭代法来计算结构的自振特性[2-3].

在计算分析中，取结构前150阶振型进行叠加，其振型参与质量之和为：纵向98.81%；横向96.75%；竖向95.04%，3个方向的振型参与质量之和均较大，因此可以达到较高的计算精度.表1和图4中分别给出了模型的前10阶自振频率与周期的计算结果和振型图.

从成桥状态前10阶振型的结果可以看出：

1）大准铁路桥整个结构的基频为0.836 112 Hz，主要振动形式为纵向振动和横向振动，且第1阶基本振型为纵向振动.在前10阶振型中横向振动出现了5次，以横桥向贡献为主，表明该桥整体横向刚度相对于其竖向、纵向刚度较弱.

2）该桥前10阶振型均未出现扭转，说明箱梁抗扭刚度较好.

3）在进行抗震设计时，由于该桥第1阶振型为纵飘，有可能在纵桥向产生较大的塑性转角，应加强塑性铰区的设计与配筋，并在此基础上要注意梁端部留有足够的位移空间.同时结构在第5阶才出现竖弯振型，表明此桥对竖向地震力具有较强的抵抗能力.

3 高低桥墩高差对自振特性的影响

在实际结构中，由于场地限制，主墩高度往往存在差异，目前对大跨度预应力混凝土连续刚构桥桥墩高差的研究多集中在高墩与低墩各自的研究上，而对高低墩之间的相互影响研究的不多，因此关注桥墩高差对连续刚构自振特性影响有现实意义[4-5].本文以大准铁路内蒙古黄河大桥主桥为对象，以49.7m墩高为基准，分别将2号桥墩高度降低0%（墩高49.7m、模型1）、4%（墩高47.7m、模型2）、8%（墩高45.7m、模型3）、12%（墩高43.7m、模型4）、16%（墩高41.7m、模型5）建立5个模型研究桥墩高差对其自振特性的影响.不同桥墩高差模型的前10阶频率、振型如表2所示，不同高差桥墩相对于等高桥墩基频的变化见图5.

表1 连续刚构桥前10阶自振频率与周期Tab.1 First ten order natural frequencies and periods of continuous rigid-frame bridge

图4 连续刚构桥的前10阶振型Fig.4 First ten order vibrationmodesof continuous rigid-fra mebridge

分析结果表明：

1）随桥墩高差增加，3个方向的自振频率增大，其中对纵向基频影响最大，桥墩高差降低到16%时，基频增加8.84%，横向基频增加3.902%，竖向基频增加2.063%，同时桥墩高差每增加2m，纵向基频基本以2%增加，横向以1%增加，竖向0.5%增加.分析桥梁结构基频增大的原因有可能是因为2号墩为较低桥墩，桥墩高度的减少有效提高了结构的刚度，并且减小了结构的自重.

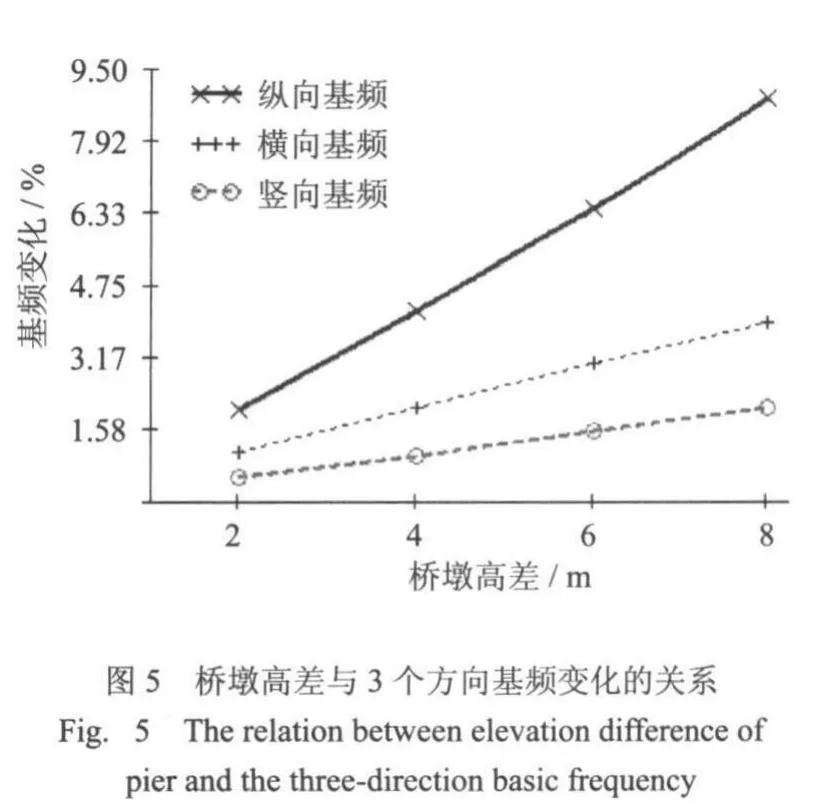
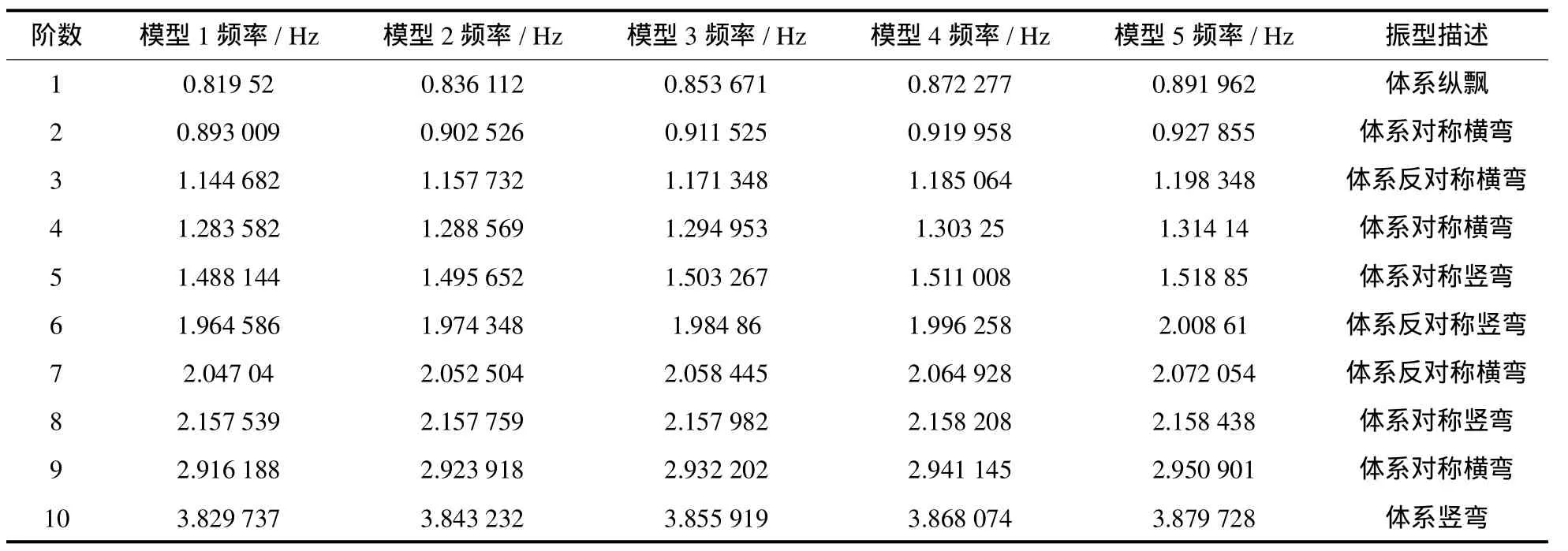
表2 5种桥墩高差下的频率与振型Tab.2 Natural frequenciesand vibration modesunder five kindsof elevation difference of pier

2）桥墩高差的变化对桥梁自振的振型形态没有影响，前10阶各振型阶次的序列也未发生变化，振型图可参考图4.

4 边中跨比对自振特性的影响

国内部分大跨度预应力混凝土连续刚构桥的边中跨比取值见表3.

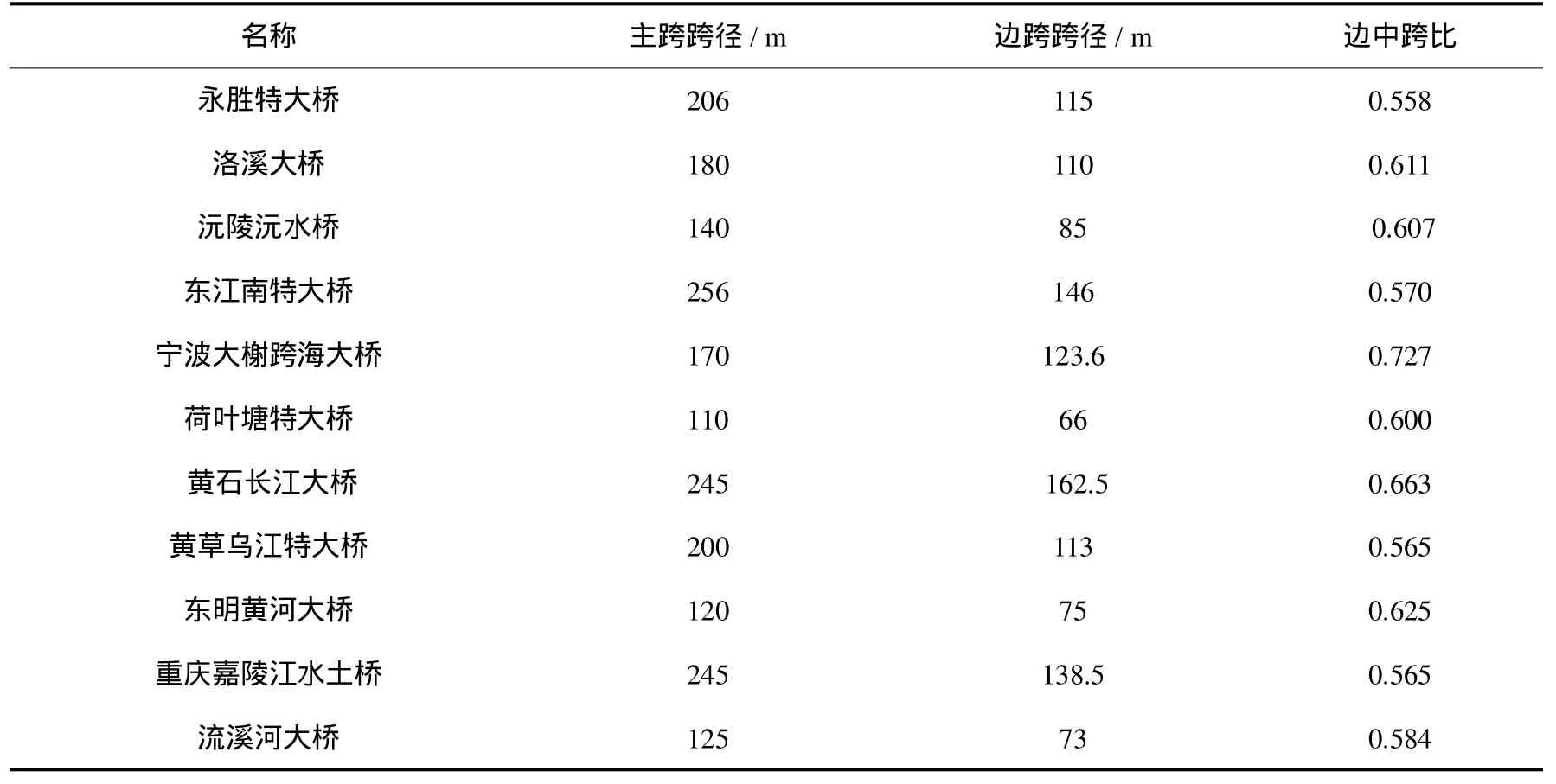
表3 国内部分刚构桥边中跨比的统计Tab.3 Statisticsof Ratio of side span tom id span of partof continuous rigid-frame bridgesathome

由表3可以看出，统计到的连续刚构桥边中跨比的平均值为0.607，边中跨比基本在均值上下浮动.

目前，对大跨度预应力混凝土连续刚构桥的研究多集中在研究边中跨比对结构受力性能的影响[6]，对研究边中跨比对其自振特性的影响很少，故本文以大准铁路内蒙古黄河大桥主桥为原始模型，在参考国内边中跨比取值经验的基础上，选取7个不同的边中跨比，分别为0.47、0.515、0.591、0.667、0.727、0.773、0.803，建立模型1～模型7，并提取7个模型的前5阶振型来分析边中跨比的变化对桥梁自振特性的影响，见表4和图6.

表4 7种不同边中跨比的频率与振型Tab.4 Natural frequenciesand vibrationmodesunder seven kindsof ratio of side span tom id span

分析结果表明：

1）边中跨比的增大引起结构3个方向固有频率都有减小的趋势.从前5阶振型中可以看出边中跨比的增大对结构纵向和竖向基频影响较大，边中跨比从0.47到0.803，纵向基频降低17.9%，竖向降低16.6%，而对横向基频的减小影响不显著，仅降低1.18%.

2）边中跨比的改变使振型序列发生较大的变化，边中跨比的增大使结构的第1阶振型发生了明显的改变，第1阶振型由对称横弯变为纵向漂移，同时从表4的振型描述中可以看出边中跨比的增大延缓了结构第一阶竖弯振型的出现.

5 结论

通过对大准铁路内蒙古黄河连续刚构特大桥主桥实例的研究分析表明：

1）此桥主要振动形式为纵向振动和横向振动，且第1阶基本振型为纵向振动.前10阶振型中横向振动出现的次数较多，表明该桥横向刚度相对其竖向、纵向刚度较弱.

2）桥墩高差增加使桥梁3个方向的自振频率增大，其中对纵向基频影响最大，对竖向基频影响最小，而对桥梁自振的振型形态没有影响，前10阶各振型阶次的序列也未发生变化.

3）边中跨比增加引起刚构桥梁3个方向自振频率都有减小趋势，对其纵向和竖向基频影响最大，同时使其振型序列发生较大差异，第1阶振型发生明显改变，由对称横弯变为纵向漂移，并延缓了桥梁竖弯振型的出现.

4）在进行此类刚构桥抗震设计时，为了提高桥梁整体刚度并改善其动力性能，在可能的情况下宜采用较大的桥墩高差，并适当减小边中跨比.

[1]王立峰，孙勇，王子强.结构参数对刚构—连续组合梁桥动力特性的影响分析 [J].东北林业大学学报，2010，38（6）：106-108.

[2]董淑喜，靳奉涛.青岛海湾大桥沧口航道桥自振特性分析 [J].公路，2009（9）：11-13.

[3]徐贤昭，董继恩，王欣南.石佛沟特大桥抗震特性探讨 [J].中外公路，2010（5）：200-203.

[4]潘强.高墩大跨连续刚构桥地震反应分析及减震措施 [D].合肥：合肥工业大学，2010.43-45.

[5]霍新.高墩大跨连续刚构桥地震反应分析 [D].北京：中国地震局地球物理研究所，2006.27-30.

[6]靳志刚，左德中.大跨度预应力混凝土连续刚构桥合理边中跨比研究 [J].交通科技，2010（3）：31-34.