非圆曲线类零件的优化加工路径

田 杨

TIAN Yang

（辽宁工程职业学院，铁岭 112000）

0 引言

在数控车加工中，往往遇到非圆曲线轴类零件的加工，例如抛物线类零件、椭圆类零件和双曲线类零件。加工这类零件大多数采用仿形后层层切削的方法，这种方法增加了走刀路线，增加了空运行时间。这里的走刀路线是指刀具刀位点相对于工件运动的轨迹，也称为进给路线，走刀路线对零件的加工质量和加工效率有着直接的影响，所以要合理的选择加工路线，应尽量使加工路线最短，以减少加工路线的距离，减少空运行的时间，提高加工效率，而且应尽量简化数学处理时的数值计算量，以简化编程工作[1]。

1 优化模型的建立[2]

1.1 抛物线类零件优化模型

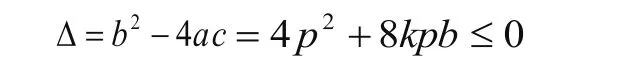
其中：k=-m/xn，m/x1，b=x2。

优化目标函数：

图1 抛物线类零件切削区域

1.2 椭圆类零件优化模型

设椭圆方程为：z2/a2+x2/b2=1，直线方程为：x=kz+w，在椭圆的上方，A点坐标为（x1，n）,B点坐标为（m, x2）。同样以/A、B点坐标确定直线方程，使切削区域剩余面积最小，即图中阴影部分面积最小。图中椭圆为已知条件，设由椭圆与x轴和z轴围成的面积为SA，直线与x=m,y=n围成的面积为SB，剩余面积为SC，则SC=m×n-SA-SB，其优化条件与抛物线方程的类似要求两方程联立后Δ≤0。因为加工椭圆类方程可能涉及到加工椭圆中心两侧的加工区域，但是因为椭圆关于x、z轴对称，所以本为只介绍椭圆中心右侧的加工路径，左侧同理。

优化目标函数：

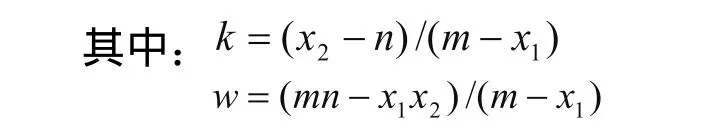
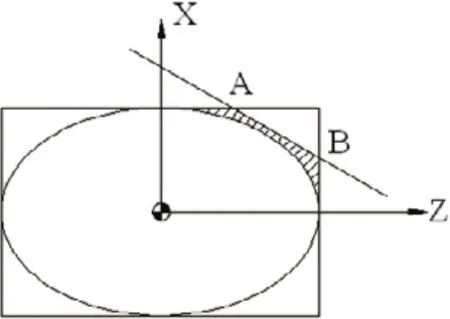
图2 椭圆类零件切削区域

1.3 双曲线类零件优化模型

设双曲线方程为z2/a2-z2/b2=1，直线方程为x=kz+w，A点坐标为（m1，n1）,B点坐标为（m2，n2），需确定点c使得切削区域三角形面积最大，也就是说剩余面积最小，由双曲线与z=m1，z=m2及x轴所围成的面积为SA，ΔABC的面积为SB，剩余面积为SC，SC=(m2-m1)(n2-n1)/2-SA-SB，设c点坐标为（x1，x1），

其优化模型为：

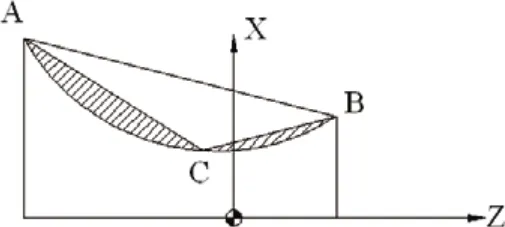
图3 双曲线类零件切削区域

2 优化路径应用[3]

本文选抛物线类零件p=20,m=10,n=10,按照优化后路径进行宏程序的编制,应用复合形法得出最优化结果为：x1=15.03，x2=5.05。抛物线类零件具体程序见表1。

3 数据对比

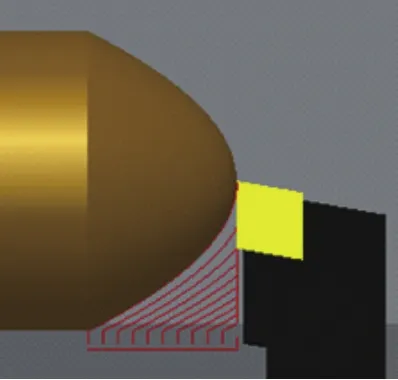
图4 仿形法加工路径

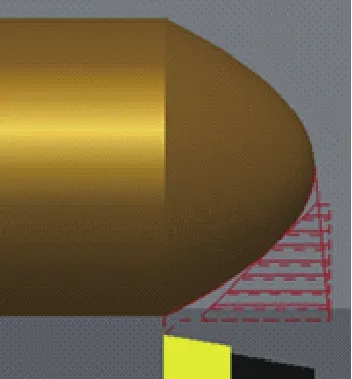
图5 优化后路径

通过仿真软件将仿形法和优化后编制程序进行仿真加工，图4为用仿形法编制程序的模拟路线图，图5为利用优化结果编制程序的路线图，在对两种方法用同样的进给量，用同样的背吃刀量的情况下，对其进行仿真加工，结果，仿形法编制的程序用时1分31秒，而用优化后编制的程序用时41秒。

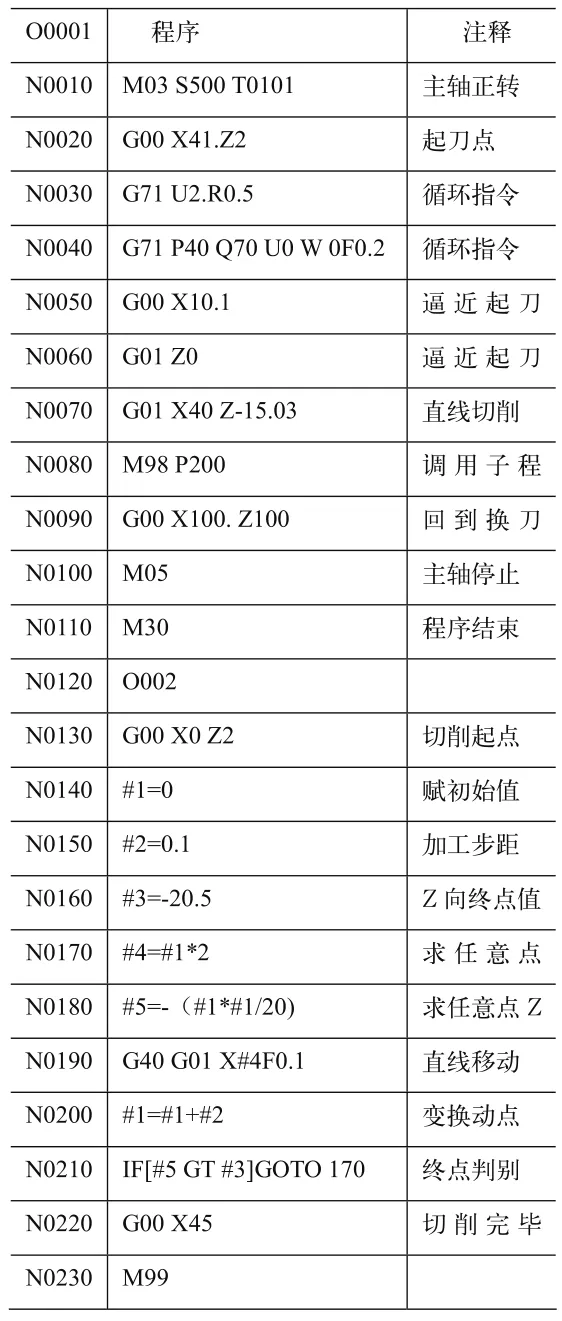
表1 抛物类零件程序

4 结论

在抛物线类零件、椭圆类零件和双曲线类零件加工中，通过以最小剩余切削面积为目标函数，建立数学模型。本文通过以抛物线为实例对其进行加工，操作简便，编程程序段少，由仿真加工对比可知优化后的路径要比仿形法编制程序运行的路径用时缩短了54%，说明加工路径缩短，提高了生产效率。

[1]何成文.基于宏程序的抛物线曲面加工程序应用研究[J].煤矿机械,2006,27(12):116-117.

[2]陈立周.机械优化设计方法[M].北京:冶金工业出版社,2004:89-124.

[3]翟瑞波.数控车床编程与操作实例[M].北京:机械工业出版社,2007:85-88.