混装生产排产序列MILP建模与仿真优化研究

蒋国璋，肖 勇，唐秋华，王 娟，雷正奇

JIANG Guo-zhang1, XIAO Yong1, TANG Qiu-hua1, WANG Juan2, LEI Zheng-qi2

(1.武汉科技大学 机械自动化学院，武汉 430081；2.东风汽车有限公司 商用车发动机厂，十堰 442000)

0 引言

随着现代科学技术的迅速发展，产品的生命周期已大大缩短，同时由于激烈的市场竞争及用户对产品的个性化要求，单品种、大批量的生产已不再适应用户对产品的多样化需求。在新的市场环境下，企业需要寻找一种新的生产模式：多产品混装生产。这种生产模式能够以大规模生产的效益进行同一类型多种产品的生产，能根据用户的需求，用大规模生产的效益完成特定产品的生产。汽车生产等以装配生产为主的企业，多采用这种混装生产模式。混装线所装配产品具有基型和多种变型产品，它们的功能和作业方式基本相同，仅仅在规格以及型号上有所区别[1]。不同产品的投产顺序影响着企业的生产和整体效率提高。因此，研究混装生产排序问题具有非常重要的意义。

1 混装生产排序问题

1.1 问题描述

汽车混装生产是在基本不改变现有生产手段、生产条件和生产能力的前提下，通过改变生产组织方式，在一定时间内，在同一条流水线上制造出多种不同型号、不同数量的产品[2]。在流水线上，每种规格的产品要经过每个工作站仅一次，在生产线上当多种不同规格的产品一起生产时，需要确定产品的加工顺序，这样就出现了排产问题。混装生产线的排产问题的焦点一般都集中在投产排序问题。

1.2 解决途径

对于混装生产最优排序问题，其解决途径如图1所示。

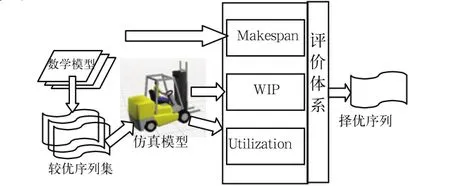
图1 基于MILP的排产序列仿真决策体系

首先我们建立混合装配流水线最小化makespan的数学模型，根据数学模型运算出部分较优序列，这样得到一个较优序列集合；然后在Flexsim中建立虚拟生产车间模型，在模型source中导入每一个较优序列，驱动仿真模型运行，得到Makespan、WIP、Utilization三个目标的实际值；最后构建关于Makespan、WIP、Utilization三个目标的评价函数D(x)，对每个较优序列进行运算，将得到的D(x)的值进行比较，最大的则为最优的投产序列。

1.3 方法的异同比较

产品的排序问题是混装生产的研究重点，Wester和Kilbridge在1963年首先对混装生产线的排序问题进行了研究。几十年来，很多学者对这个问题进行了大量的研究。对这些问题的研究，学者们主要是集中在目标函数的优化与排产方法的优化。本文的不同点在于对排产的优化是基于目标函数和Flexsim仿真验证相结合的优化，并通过优化找出最优的排产序列。

2 基于MILP的混装生产排产优化数学模型

装配线平衡下的混合装配线排产优化问题能够描述为确定M个品种的D个产品在计划期内的投产顺序，优化混合装配线的预定排产目标[4]。这里建立混合装配流水线最小化makespan的数学模型。

1）模型参数：i：产品投产顺序编号；j：工位代号；N：总装配线上工位总数；C：流水线的节拍；n'：产品的作业元素的个数；E：作业元素的集合，。任意的记是作业元素 的直接优先元素的集合。：第m种产品的第 个作业元素的时间；所有M种产品的第 个作业元素的平均时间。

混装流水生产线的优化模型为：

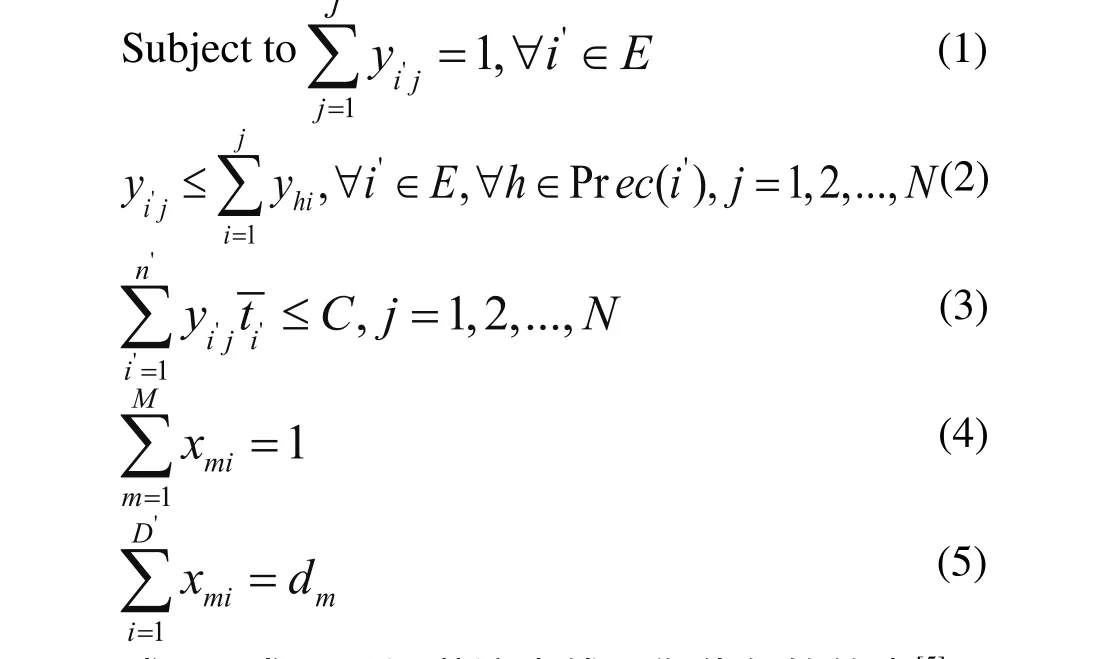
式(1)～式(3)是混装流水线平衡优化的约束[5]，其中，式(1)保证一个作业元素分配在一个有且只有在一个工作站内；式(2)表示只有当一个作业元素的所有直接优先元素全部被分配到工作站内时，则这个作业元素才能被分配；式(3)保证分配到一个工作站内的每一个作业元素的平均作业时间不能超过给定的节拍；式(4)和(5)表示混装生产线的排序优化约束[5]，其中，式(4)保证在排序序列的一个位置上有且仅有一个m型产品；式(5)保证在排序序列的所有位置上某一种产品的数量恰好为这种产品的需求量。

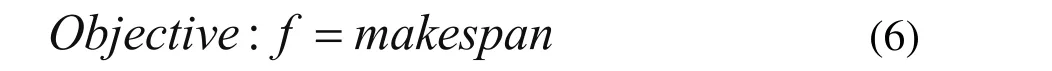
式(6)是要优化的目标函数，其计算方法如下：

每个循环开始时，第1个投产的产品在第1个工位上的开始时刻记为0，即S11=0。第个投产的产品在第个工位开始加工的时刻为：

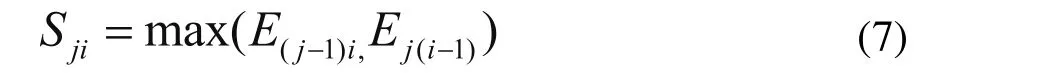
式（7）中第i个产品在第j个工位的开始时刻为第i个产品在第(j-1)工位加工的结束时刻与第(i-1)个产品在第j个工位加工的结束时刻之间的较大值。

式(8)中第i个产品在第j个工位的结束时刻为m型中的第i个投产产品在第j个工位的加工时间与第i个产品在第j个工位的开始时刻之和。

依此类推可知：排产序列中第D'个产品在第N个工作站的开始加工时间SND和结束时刻END为：

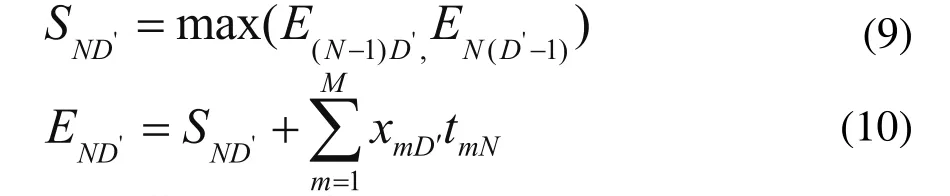
一个排产循环中，生产制造周期为：

3 混装排产方案评价

3.1 评价指标

1）制造周期(makespan)

制造周期(makespan)是指一个最小生产循环中，从第一个工件开始进入生产到最后一个工件加工完成所需的总时间[6]。使用不同的投产序列，makespan也会不同。对于基于时间竞争的企业来说，makespan的优化等于压缩了供应链的制造周期，这样使整个供应链实现快速响应，从而成为企业的新的竞争优势来源。

2）在制品（WIP）值

在制品（WIP）是指某一时刻所有已投入生产线但尚未完成最后加工步骤的工件。对于整条生产线来说，在制品不能太多，也不能太少。太多,会导致产品的加工周期变长，使生产效率低下；太少，会使大量机器处于空闲状态，导致资源的浪费。

3）设备利用率(utilization)

设备利用率指设备在开机状态下用于实际加工工件的时间占开机时间的比例[6]，即：

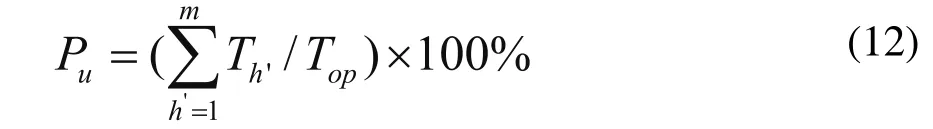
设备利用率反映系统的忙闲程度。发动机生产设备投资庞大，运作成本高，使得投资者不愿意任何一台设备闲置，于是不断追求所有设备的完全利用。

3.2 评价方法

根据以上三个评价指标，运用系统工程学中功效系数法，以上评价指标对应的目标函数分别为，功效系数为di，且分别构建不同的功效函数

制造周期(makespan) 的功效函数为：

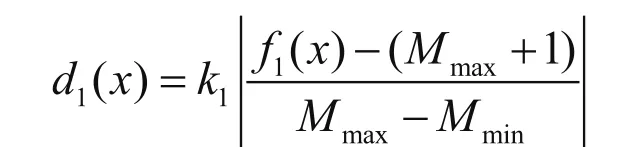
在制品（WIP）的功效函数为：

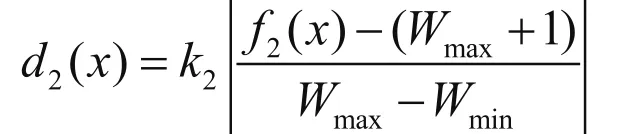
设备利用率(utilization) 的功效函数为：

其中k1,k2,k3,为权重系数，k1+k2+k3=1，取k1=0.5,k2=0.3,k3=0.2。求的几何平均值。则评价体系函数为：

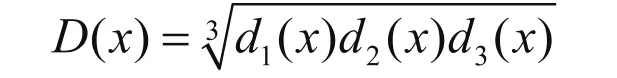
4 基于Flexsim的混装生产系统仿真

4.1 生产环境建模

对于发动机制造车间，我们只以油漆混流生产线为例进行排产顺序分析。整条油漆生产线为12台串行处理器，运用Flexsim软件，在实体库中拖入相应的实体，对每个实体进行相应的设置，油漆线生产线仿真布局图如图2所示。

图2 油漆线生产线仿真布局图

4.2 制造流程仿真

仿真就是要得到有意义的仿真结果,所以要有针对性地建立与生产过程有关的模型，而对于生产过程无关或者对生产过程影响不大的设备、过程等进行简化[7]。该汽车发动机两种产品（D、H）的总成装配生产线流程分别为：

3/4装配→油漆→1/4装配→测试→环境

3/4装配→1/4装配→测试→油漆→环境

4.3 制造过程控制仿真

针对不同的方案，设置模型中的对象参数，其中source 1表示上游生产线运送到下游的半成品发生器，source每隔7.5min投放一产品，对其进行不同方案的投产序列设置。然后对不同类型的产品赋予不同的颜色，On Exit 程序设置如下：

在整条油漆生产线中，每个处理器对产品D的处理时间设置为7.5min，对产品H的处理时间设置为6min。程序设置如下：

5 仿真实例与分析

为了降低在制品数和生产线缓存，需要优化不同品种产品的排产顺序。以其油漆混流生产线为例，其生产线需要生产D、H两种型号的发动机。需要构造全部可行排产序列，寻找最优的作业方案。

某日需求量为：D型60台、H型45台。采用循环排序法，将需求集{60，45}各个元素除以最大公约数15得到一个集合{4，3}即为最小比例集。在排产操作中，只需对最小比例集{4，3)中的共7个产品排序。通过已建立的最小化Makespan的数学模型，得出如下4种可能的最优投产排序方案：方案1：D-D-D-D-H-H-H;方案2：D-H-H-D-DH-D;方案3：D-D-H-D-H-D-H;方案4：H-H-D-D-HD-D。

在实际投入生产之前，用Flexsim软件对4种投产顺序进行仿真。参数设置完成后，先编译，验证无误后仿真运行。以方案1:D-D-D-D-H-H-H为例，其中红色代表产品D，绿色代表产品H,模型运行效果如图3所示。

图3 油漆生产线运行效果图

对4种不同的投产方案进行模型运行后，对数据进行统计。随机选取处理器8，对4种不同的方案进行运行后，运行时间设置为300min，比较制造周期的大小，生产线的缓存大小和处理器8的工作效率。运行数据如表1所示。

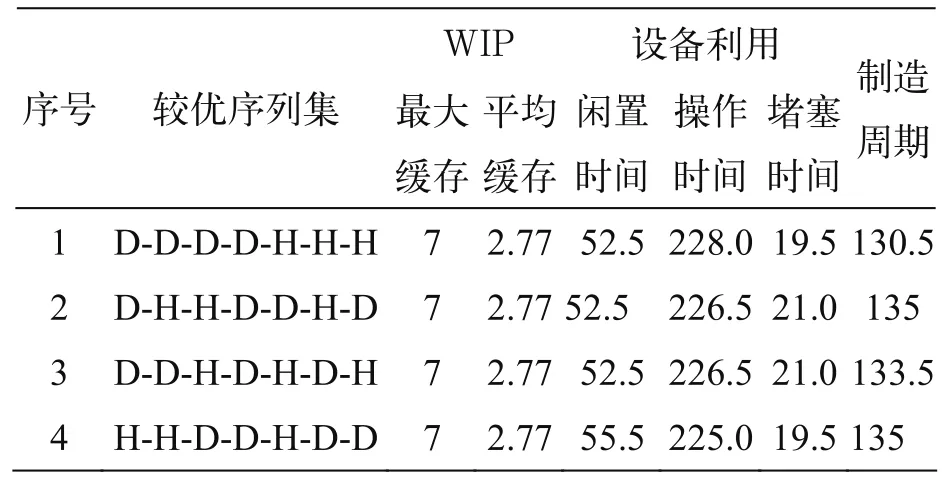
表1 方案运行数据

以方案1为例，制造周期(makespan)的功效函数为：

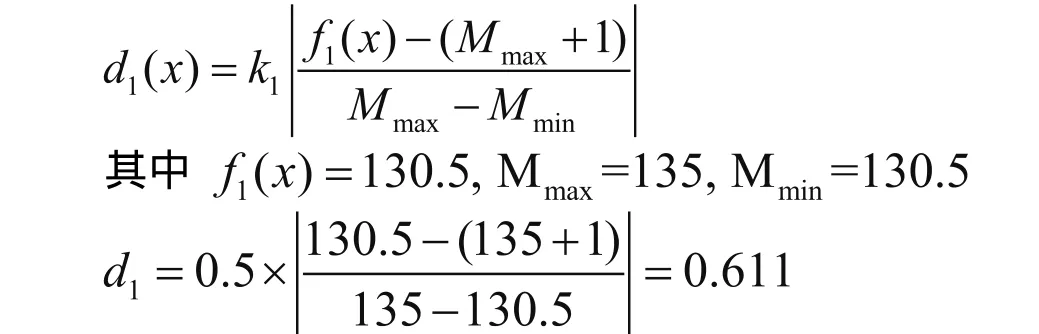
在制品（WIP）的功效函数为：

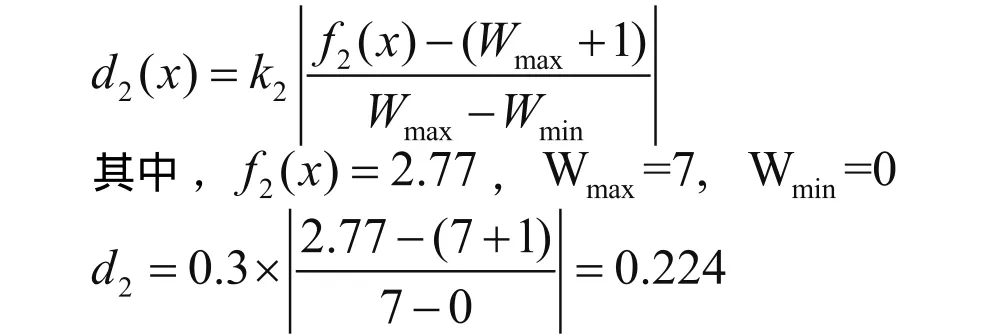
设备利用率(utilization) 的功效函数为：

比较以上4种方案，可知D1为最大值，故方案1为最优方案。

6 结束语

汽车发动机制造车间生产排序是一个非常复杂的离散动态事件。采用建立虚拟生产车间模型进行仿真的方法能够节省车间调度的验证成本，并且能够很大程度上反映生产车间的实际情况。

针对发动机车间的调度问题，首先通过建立MILP数学模型，得出可能的最优排产方案，然后使用Flexsim软件建立虚拟生产环境，对不同品种产品的投产序列进行仿真验证。对得出的实验结果进行分析，建立评价函数，比较计算结果，从而能够找出最优的排产方案。说明利用MILP数学建模与Flexsim建模相结合的优化方法，能够为企业生产线排产提供理论依据。

[1]唐秋华,席忠民,陈平和,严运兵.混装线投产序列和工位任务的协同调度机理[J].工业工程,2008,11(1):20-24.

[2]刘飞.CIMS制造自动化[M].北京:机械工业出版社,l997.

[3]Stefan Voβ,Andreas Witt.Hybrid flow shop scheduling as a multi-mode multi-project scheduling problem with batching requirements:A real-world application[J].Int.J.Production Economics,2007,105:445-458.

[4]Kim Y K,Hyun C J,Kim Y.Sequencing in mixed model assembly lines:A genetic algorithm approach[J].Computers＆Operation Research,1996,23(12):1131-1145.

[5]宋华明,马士华.混合装配流水线上最小makespan的协同优化[J].系统工程理论与实践,2007,27(2):154-160.

[6]乔非,许潇红,方明,吴启迪.半导体晶圆生产线调度的性能指标体系研究[J].同济大学学报,2007,35(4):538-542.

[7]赵建辉,王红军.基于Flexsim的混流装配线投产顺序的仿真[J].微计算机息,2007,23(24):29-31.