基于有限元技术曲轴的动力学性能分析

宋晓玲

SONG Xiao-ling

（洛阳理工学院，洛阳 471000）

1 曲轴动力学分析的基本理论

在发动机中曲轴是主要的旋转机件，通过连杆可以把活塞上下的往复运动转变为循环旋转运动。因此曲轴的动力学性能对于发动机的可靠性以及使用寿命都有着决定性的影响，它是发动机中主要运动部件之一。曲轴在工作过程中的受力情况是非常复杂的，它需要同时承受周期性变化的气缸爆发压力、活塞连杆组往复惯性力、旋转惯性力、附件不规则阻力矩以及外界作用力等多种荷载作用。长期在这种环境中工作，很容易造成曲轴的动应力集中，从而产生疲劳裂纹导致曲轴断裂失效，并且由于曲轴的关键作用它的失效还会产生更严重的影响。随着发动机功率以及性能的不断强化，使得曲轴的工作条件也越来越苛刻，所以曲轴的保护工作显得尤为重要，需要通过一系列研究对其动力学性能有更加细致的了解，为曲轴结构的优化设计提供可靠的理论依据。

在对发动机开发的过程中，针对曲轴在使用上的重要性需要用先进的计算方法进行设计，目前使用最为普遍的是以有限元技术作为研究的主要方法，有限元技术能够使曲轴计算分析的结果更加精确。利用有限元技术建立曲轴的有限元模型，模拟曲轴的真实边界条件进行模态分析，从而获得曲轴前六阶固有频率以及振型，然后再对曲轴进行瞬态动力学分析，获得了曲轴前端、后端的角位移以及应力随曲轴转速的变化规律，对于曲轴的结构设计、制造以及维护都具有现实意义。

2 曲轴有限元模型的建立

利用有限元技术对曲轴的动力学性能进行计算的过程中，由于曲轴的有限元模型包含数十万甚至上百万个自由度，如果将这些自由度直接进行动力学性能分析，庞大的计算量无疑会增加计算的复杂性的从而影响其精确度，通常需要采用模态缩减的方法来简化计算过程，减少运算时间并且提高计算精确度。首先对于一个柔性体有限元系统，进行模态缩减时其动力学方程表示为：

式中M为质量矩阵，K为刚度矩阵，F（t）为外载荷量。由此可知如果该柔性体有限元系统包含的节点很多（A量级），那么M、K的规模将会很大（A2量级），如果直接按照上式的方程进行求解，如此庞大的数据量不仅对于计算系统有着很高的要求，而且一般情况下完全进行计算是根本无法实现的。但是由于外载荷向量[F（t）]中一般只是一些为数不多的非零元素，而将这些非零元素所在行的自由度定义成边界自由度，即直接受到荷载作用的自由度方向u。系统内部其它的自由度则为内部自由度，通过对上式方程进行适当的转变可以得到：

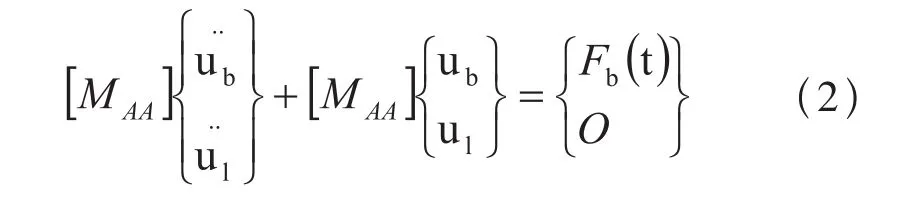
然后再定义一个变换矩阵如下所示：

此矩阵对应的变换为：

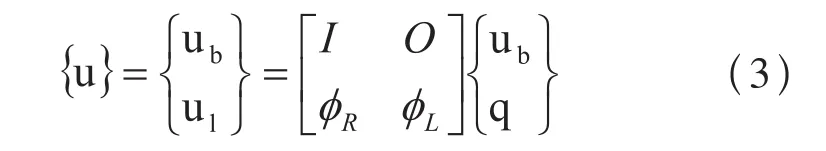
式中ub指边界自由度，ul指内部自由度，φR指刚体向量组，q指模态自由度，φL指内部自由度的模态振型。这种变换被称为Craig-Bampton变换，该变换的矩阵称为CB矩阵φcb。将（3）式代入（2）式中可得：

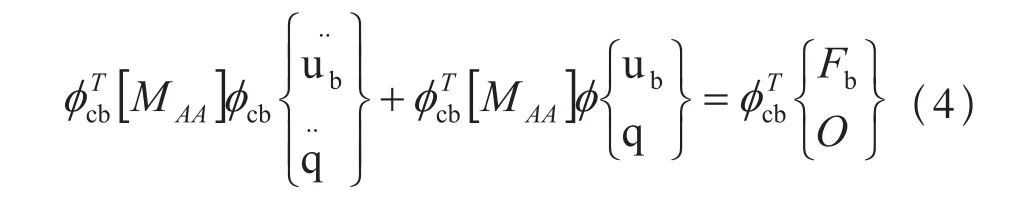
根据CB矩阵的定义，可以将（4）式转变成为：

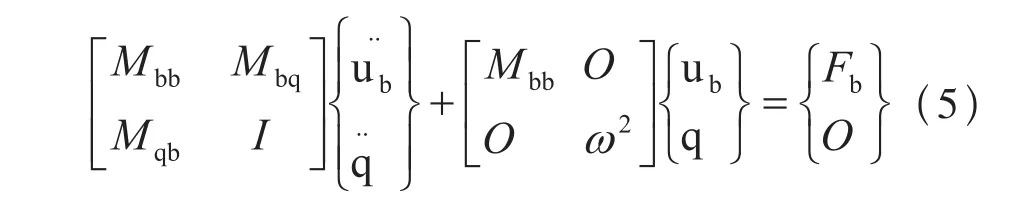
由于模态阶数越高，模态自由度的幅度越小，即可以忽略高于一定阶次的模态运动。因此，对于（5）式，只需要根据实际情况考虑保留前面数个或者数十个模态自由度的方程即可，这样方程的综述便从数十万到上百万个缩减到数十个了，通过求解保留下来的数十个方程组成的方程组，便能得出模态系统的全过程响应，在利用CB逆变换，便能恢复出物理系统所有节点的响应全过程。

然后利用有限元技术建立曲轴有限元模型如图1所示。在曲轴主要受力点包括扭转减振器、凸轮驱动链轮、主轴承、曲柄销以及飞轮等区域建立RBE3约束。由于RBE3约束的参考点并不是独立的，所以需要在参考点设置附属点，然后将参考点与对应的附属点在六个自由度方向上用刚度很大的弹簧绑定，根据实际情况定义了这些附属节点的边界自由度，如表1所示。

图1 曲轴有限元模型

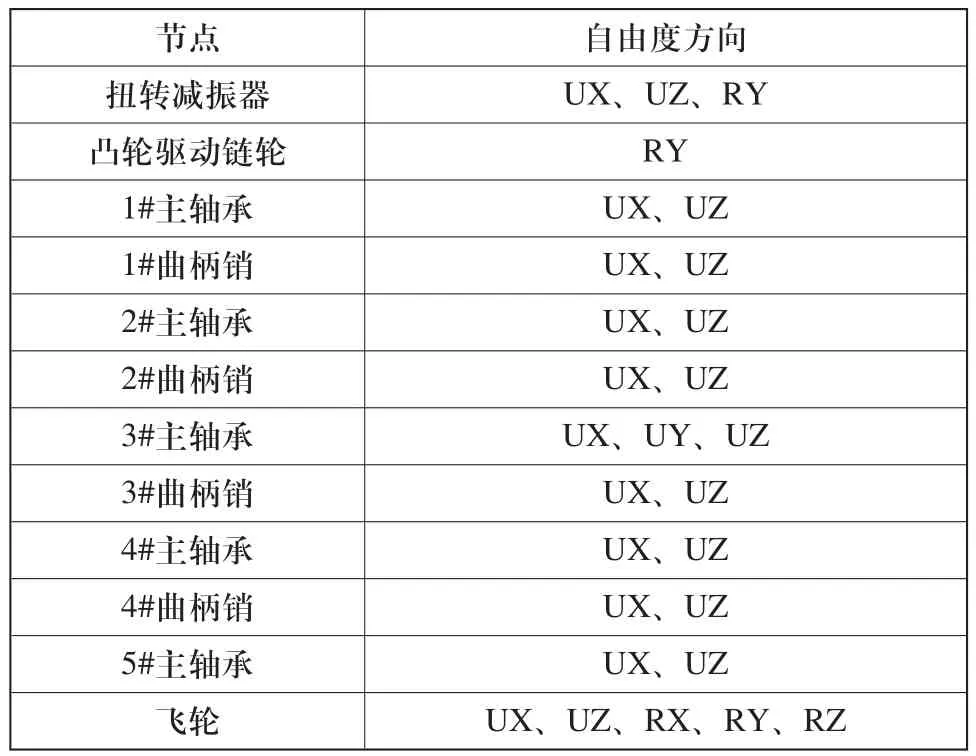
表1 边界自由度列表

曲轴有限元模型的建立包括曲轴柔性体、曲轴皮带轮、飞轮、主轴承、曲柄销和连杆轴等多个部件以及运动副组成。对于柔性体模型，主要通过离散的有限元建立模型，利用软件结合有限元模型的组成与各部件的约束关系建立以曲轴系统有动力学方程并进行求解计算；对于刚体模型，建立动力学微分方程进行描述，曲轴的零部件位置，质量以及转动量等都可以通过CAD软件建立三维模型。

3 曲轴的模态分析

发动机在工作时往往能够达到很高的转速，使曲轴周期性荷载的作用力加大，如果在设计上考虑不足，曲轴与发动机在工作当中产生强烈的共振致使动应力急速增加，长期在这种环境中工作很容易造成曲轴的动应力集中，从而产生疲劳裂纹导致曲轴断裂失效，并且由于曲轴是发动机的主要运动部件，它的失效还会产生更严重的影响，所以需要通过模态分析确定曲轴前六阶固有频率以及振幅。对于发动机而言，只有较低的频率才会引发较大的振动，所以曲轴较低的固有频率对系统的响应影响较大，本文主要研究曲轴前六阶固有频率以及振幅如图2～图7所示。

然后曲轴前六阶固有频率以及振幅的特点总结如表2所示，从表中曲轴振型描述中可知曲轴第一、二阶非零振型分别是在X以及Y方向作一阶弯曲振动；第三、四阶非零振型分别是在X以及Y方向作二阶弯曲振动；第五阶非零振型主要是纵向扭振；第六阶非零振型为纵向扭振加弯曲振动。

图2 一阶非零振型

图3 二阶非零振型

图4 三阶非零振型

图5 四阶非零振型

图6 五阶非零振型

图7 六阶非零振型

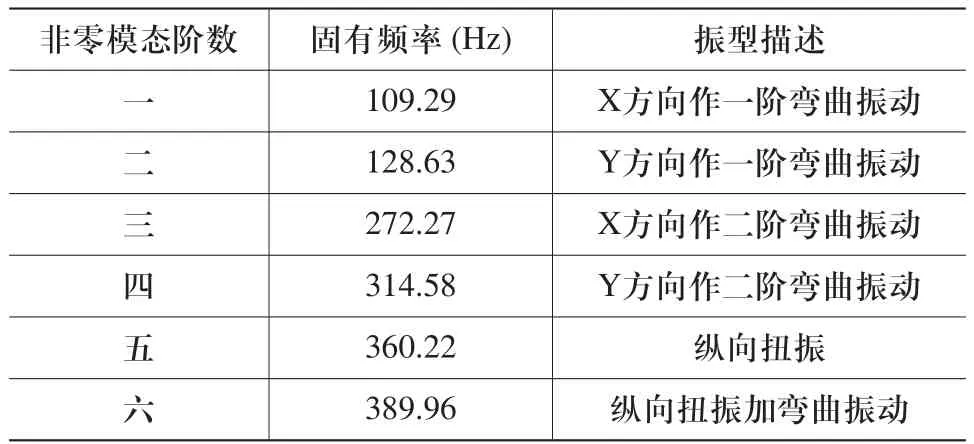
表2 曲轴前六阶固有频率和振幅描述

除此以外，发动机对外输出的有效转矩是指曲轴角位移的乘积，在曲轴工作过程中，曲轴前后端的角位移变化以及各个点的应力分布具有一定的随机性质，因此需要通过瞬态动力学分析确定曲轴前端、后端的角位移以及应力随时间以及转速变化所发生的相应。由于发动机通常都在高转速的环境下工作室能达到很高的转速，因此在计算曲轴对外荷载的响应时，必须将时间变量考虑在内，使用瞬态动力学分析时，通过输入时间以及转动函数的载荷，可以获得随时间以及转动变化的应力以及应变，瞬态动力学分析的运动方程和通用运动方程相同即为 ，然后施加时间历程载荷进行求解，有结果可以得到一系列的载荷循环历程如图8、图9所示：

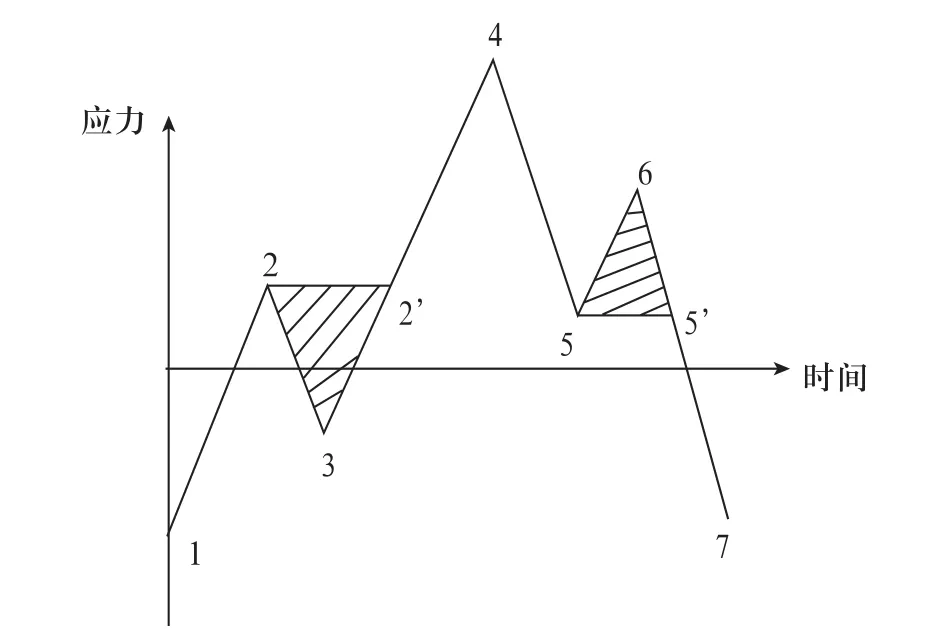
图8 应力—时间历程图

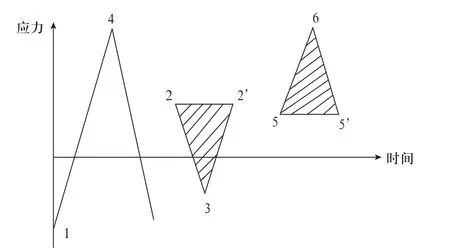
图9 应力—时间历程简化模式

由此进行分析，可以得到曲轴前端、后端的角位移和应力随曲轴转速的变化规律，并且基于此对曲轴进行损伤评估，进一步得到可靠的曲轴动力学参数以及疲劳安全状况，可以在设计的过程中及时发现存在的问题并进行优化，极大的减少试验次数以及费用，为曲轴的制造以及维护提供了有利的理论依据。

4 结束语

综上所述，现阶段在曲轴的设计制造过程当中主要运用的是有限元技术对其进行动力学分析。利用有限元技术建立曲轴的动力学模型，然后进行模态分析，获得了曲轴前六阶固有频率和振幅，结合瞬态动力学分析能够发现曲轴前端、后端的角位移以及应力变化随着曲轴的转速增加而增大，并且容易导致疲劳失效的风险以及其它潜在问题。根据有限元技术对曲轴进行分析，提出一些具有针对性的优化方案，为曲轴的改进设计提供了方向，并且有效地缩减了曲轴等关键部位的的开发周期与制造成本，大大提升了设计的质量。

[1]程晓鸣. 基于虚拟技术的曲轴系统多体动力学研究[D].天津大学, 2006.

[2]鱼春燕.曲轴性能分析及其优化设计[D].江苏大学, 2005.

[3]刘波. 曲轴参数化建模和有限元分析[D]. 武汉理工大学,2006.

[4]程晓鸣. 基于虚拟技术的曲轴系统多体动力学研究[D].天津大学, 2006.

[5]张国庆, 黄伯超, 浦耿强, 王成焘. 基于动力学仿真和有限元分析的曲轴疲劳寿命计算[J]. 内燃机工程, 2006.