开关延迟对Buck变换器分岔的影响

金爱娟， 陈 明， 李少龙

（上海理工大学 光电信息与计算机工程学院，上海 200093）

电力电子电路容易发生各种非线性现象，如分岔、混沌等，直接影响变换器的稳定性和可靠性［1］.国内外学者对DC－DC变换器的分岔和混沌现象已经作了大量的研究，在变换器中发现存在分岔和混沌现象［2－9］，已经建立了数学模型［10－12］，并探讨了混沌的控制和反控制技术［13－14］.然而，一般的文献都假设功率开关管工作在理想的开关状态下，没有考虑开关延迟对系统分岔和混沌的影响［1－15］.很多文献都将电路工作频率设定为几十千赫以下［4－10］，这种情况下几微秒的开关延迟对电路的影响可以忽略.但是，为了提高系统的性能，开关频率一般都工作在几百千赫以上，在这种情况下，开关延迟的影响不容忽视，它的大小可能改变系统的分岔结构甚至稳定性.本文通过大量的计算机仿真数据对一个典型Buck电路在开关延迟影响下的分岔和混沌现象进行分析，为变换器的研究和设计提供参考.

1 系统数学模型的建立

图1是电流模式控制Buck变换器的原理图.用一个频率固定的时钟脉冲信号影响触发器的输出信号，从而改变开关状态，在每个时钟周期的起始时刻输出开关导通信号.将电感电流与参考电流相比较，当电感电流达到参考电流值时，输出开关关断信号.存在开关延迟时，触发器输出开关导通和关断信号以后，开关不能马上动作，存在滞后响应.

电感电流i和电容电压vc设定为系统的状态变量.假设Vin为理想直流电压.导通和关断期间状态变量的关系可以通过线性微分方程组来描述.

开关导通期间

式中，L为电感，C为电容，R为电阻.

开关关断期间，连续电流（CCM）模式下

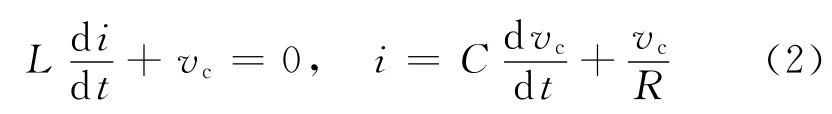
在理想开关和存在开关延迟的情况，导通和关断期间的方程组是一样的，所求解的微分方程的初始值和区间不同.具体的工作状态可以参考后面的电感电流时域图.

图1 电流模式控制Buck变换器的原理图Fig.1 Schematic diagram of a current－mode controlled Buck converter

2 仿真结果

根据图1搭建Matlab电路仿真模型，参数取值为：参考电流iref＝1A，电阻值R＝10Ω，电感值L＝0.4mH，电容值C＝1mF，时钟频率为200kHz，输入电压直流分量的变化范围为10～25V.假设开关管的导通和延迟时间相同.

在文献［16］中，仿真计算使用的算法精度达到10－10，但是，仿真出来的分岔图和庞加莱截面图存在异常数据，文献解释是由于计算机精度引起的计算误差.文献［10］中也提到，由于Buck变换器工作模态的复杂性，它的分岔和混沌建模一直是一个困难的问题，微小差异的参数可能导致截然不同的分析结果，使得出结论的真实性受到质疑.为了提高数据的准确性和可靠性，本文在仿真计算中将精度提高到10－13，从各种仿真数据图上可以观察到，没有出现异常的数据点，进一步提高计算精度后，混沌图没有变化.本文所给出的混沌图中每一个输入电压值对应的周期采样电感电流值和庞加莱截面图中的数据点均是在系统完全稳定以后取出最后500个仿真数据点所形成的.

如图2所示，输入电压为20V，开关延迟时间Td与时钟周期T的比值以0.02的步长增加时，周期采样电感电流iT从稳定值到2倍周期、3倍周期分岔变化，跳跃点发生在0.14和0.38处.由图2可见，开关延迟时间增大会影响到系统的稳定性，甚至进入分岔和混沌状态.由于实际器件的开关延迟时间不是一个稳定的参数，所以，在设计系统选择器件时必须适当考虑一定的安全系数.

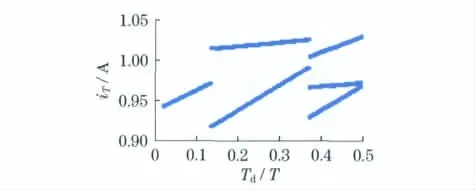
图2 开关延迟时间对分岔结构的影响Fig.2 Influence of switching delay on bifurcation structure

图3显示了开关延迟时间分别为0，0.5，1，2μs这4种不同情况下，以输入直流电压作为变量的混沌图，输入电压值的步长为0.1 V.为了观察开关延迟时间对系统的影响，在图3中，分别对不同开关延迟时间的混沌图进行对比分析，在图3（b）、3（c）和3（d）中，仅仅改变开关延迟时间的大小，其它参数不变.随着开关延迟时间的增大，混沌区域内的窗口有所变化，分岔结构发生了较大的改变，分岔周期数也在增加.如图3（d）所示，已经不是图3（a）所示的标准倍周期分岔，而是3倍周期分岔.

对于其它电路参数的研究，选取图3个别输入电压对应的参数进行详细分析，其它的情况可以依此类推.

图3 以输入直流电压为变量的混沌图Fig.3 Chaos diagrams with DC input voltage as a variable

图4是在Vin＝24V，开关延迟为0.5μs时的一系列波形图.由于存在0.5μs的开关延迟，导致图4（d）电感电流的最大值大于参考电流值，图中的三角形数据是时钟脉冲对应的采样点.在电路稳定以后的庞加莱截面图如图4（a）所示，即使采用理想器件和高精度计算，周期采样电感电流值也不是高精度稳定的.

图5是在Vin＝12 V，开关延迟为1μs时的一系列波形图.在图5中，系统在过渡期出现标准倍周期分岔，稳定以后的周期采样电感电流呈现一种无序的混沌状态.在图5（a）的庞加莱截面图中，数据点的分布疏密不同，但是，在长期的行为中很难发现其规律.从图5（d）可以看到变换器在不同区间开关的工作状态，上升曲线是开关导通阶段，下降曲线是开关关断的电流连续阶段，没有出现电流不连续阶段.电流不连续阶段只有在开关频率较低或开关延迟增加到一定时间以后才会出现.

图6（见下页）是在Vin＝18V，开关延迟为1μs时的一系列波形图.图6（a）的庞加莱截面图是左右两块形状相似的条形结构，从左到右6条数据的点数是37，125，88，37，125和88.系统处于分岔状态时出现的庞加莱截面图可能是环形或其它结构，有可能完全相同，也有可能不同，这取决于系统参数的变化.图6（d）的三角形数据点是周期采样电感电流，其数值范围如图6（a）和6（b）所示，在0.034 s以后倍周期分岔的每一分支产生3倍周期分岔，呈现出6分岔的结构，6个电流值在大范围内虽然存在一定的比例关系，但是，数据的出现没有严格的规律，在小范围内则按照一定的频率比和次序有规律地轮流出现，在无序中呈现出有序.复相同的轨迹，周期采样电感电流值是一个标准的倍周期分岔结构，两个不同的电流值轮流出现，如图7（b）和7（d）所示.

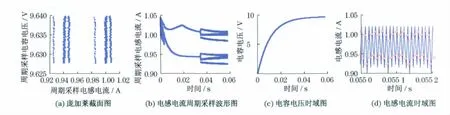
图6 Vin＝18V，开关延迟1μs时的波形图Fig.6 Diagrams for Vin＝18Vwith 1μs switching delay

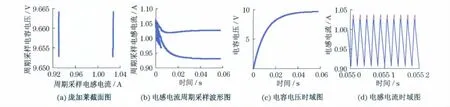
图7 Vin＝24V，开关延迟1μs时的波形图Fig.7 Diagrams for Vin＝24Vwith 1μs switching delay

从图4（c）、5（c）、6（c）和7（c）中可以发现，不管电感电流处于稳定、分岔还是混沌状态，电容电压在系统稳定后的值基本相等.从这个现象来看，在设计系统时，可以根据实际情况将电感电流置于稳定、分岔或混沌状态，对输出电压的影响不大.

3 结 论

采用大量的计算机仿真实验数据对电流模式控制Buck变换器在理想开关和3种典型开关延迟的分岔和混沌图进行对比分析，并针对不同的工作点，通过庞加莱截面图、电流和电压波形图进行比较和分析.当系统的开关频率较高且存在开关延迟或控制滞后时，可能引起分岔结构较大的变化.随着开关延迟的增加，系统参数从稳定向倍周期和多倍周期分岔发展，导致系统出现非预期的运动状态，甚至不稳定.本文的结论对其它拓扑结构的变换器在开关延迟或其它非理想电路参数的分析和研究上具有一定的参考作用.

［1］Yao Y，Fassinou F，Hu T，Stability and robust regulation of battery driven boost converter with simple feedback［J］.IEEE Transactions on Power Electronics，2011，26（9）：2614－2616.

［2］王学梅，张波.H桥直流斩波变换器边界碰撞分岔和混沌研究［J］.中国电机工程学报，2009，29（9）：22－27.

［3］周宇飞，丘水生，陈军宁.滞环电流模式控制Cúk变换器的非线性现象研究［J］.中国电机工程学报，2004，24（3）：96－101.

［4］吴俊娟，邬伟扬，孙孝峰.并联Buck变换器中的混沌研究［J］.中国电机工程学报，2005，25（22）：51－55.

［5］陈明亮，马伟明.多级并联电流反馈型DC－DC升压变换器中的分岔与混沌［J］.中国电机工程学报，2005，25（3）：67－70.

［6］马西奎，刘伟增，张浩.快时标意义下Boost PFC变换器中的分岔与混沌现象分析［J］.中国电机工程学报，2005，25（5）：61－67.

［7］周宇飞，陈军宁.电流模式控制Boost变换器中的切分叉及阵发混沌现象［J］.中国电机工程学报，2005，25（1）：23－26.

［8］刘伟增，张浩，马西奎.基于频闪映射的Boost PFC变换器中的间歇性分岔和混沌现象分析［J］.中国电机工程学报，2005，25（1）：43－48.

［9］张波，齐群.PWM Buck变换器不同工作方式下的次谐波和混沌行为［J］.中国电机工程学报，2002，22（10）：18－21.

［10］张波，曲颖.Buck DC／DC变换器分岔和混沌精确离散模型及实验研究［J］.中国电机工程学报，2003，23（12）：99－103.

［11］张波，李萍，齐群.DC－DC变换器分叉和混沌现象的建模和分析方法［J］.中国电机工程学报，2002，22（11）：81－86.

［12］李虹，张波.DC－DC开关变换器中混沌映射的不变分布求解及其应用［J］.中国电机工程学报，2005，25（23）：54－60.

［13］杨汝，张波.开关变换器混沌PWM抑制EMI的机理和实验研究［J］.中国电机工程学报，2007，27（10）：114－119.

［14］李志忠，丘水生，陈艳峰.混沌映射抑制DC－DC变换器EMI水平的实验研究［［J］.中国电机工程学报，2006，26（5）：76－81.

［15］Wang Yuanbin.Research on chaos in switching DC－DC converters［C］∥Intelligent Computation Technology and Automation，2009，3：91－94.

［16］朱雪丰，徐冬亮，舒秀发，等.Buck转换器中的分岔与混沌研究 ［J］.系统仿真学报，2007，19（15）：3387－3389.