一个新的三维混沌系统
刘汝臣
(辽宁省交通高等专科学校,辽宁沈阳110122)
由于混沌系统有1个正的Lyapunov指数,其动力学行为复杂,在非线性科学以及其他工程领域和社会科学领域得到了广泛的应用.自从1963年Lorenz[1]在分析气候数据时发现第一个混沌吸引子以来,后来人们称之为Lorenz系统.许多科研工作者对混沌的生成产生了浓厚的兴趣,不断地对Lorenz系统改进变形得到好多新的混沌系统[2-10].这些新混沌系统的不断被发现,一方面丰富了混沌系统的数量,另一方面在混沌保密通讯方面以及控制和同步方面也有较广泛的应用.所以构造新的混沌系统是非常有好处的.
本文通过计算机数值计算Lyapunov指数构造了一个新的混沌系统,通过一系列常规分析方法分析了系统的丰富的动力学行为.
1 混沌模型及其混沌吸引子
本文中所构造的新混沌系统数学模型为:

这是一个非线性常微分方程组,其中x,y,z为系统的状态变量,a,b为系统的参数.当参数a=0.11,b=0.3时,利用 Wolf方法数值计算系统的三个 Lyapunov指数为 λ1=0.0647,λ2=-0.0023,λ3=-1.0331,说明此时系统处于混沌状态,图1给出了当参数a=0.11,b=0.3的混沌吸引子相图,轨线相互缠绕,动力学行为比较复杂.但目前轨线方程的计算还没有方法.
2 新混沌系统的基本动力学分析
2.1 时间响应
对于非线性系统而言,从时间相应图上看状态值如果无规律的在一定范围内变化,说明系统可能在做混沌运动.图2给出了当参数a=0.11,b=0.3时系统的三个状态变量的时间响应图.

图1 当参数a=0.11,b=0.3时系统的混沌吸引子 (a)xy平面;(b)xz平面;(c)yz平面Fig.1 Chaotic attractors of system when a=0.11,b=0.3(a)xy plane;(b)xz plane;(c)yz plane
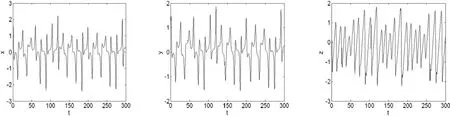
图2 系统的时间响应图(a)tx;(b)ty;(c)tzFig.2 Time responsedigram of the system(a)tx;(b)ty;(c)tz
2.2 平衡点及其稳定性
2.3 典型参数对系统运动状态的影响
为了进一步研究系统参数变化时系统的运动变化情况.图3给出了固定参数b=0.3,系统随参数a∈[0,0.23]变化关于x的分岔图和Lyapunov指数谱图,几个典型参数下的周期轨如图4所示.

图3 系统随参数a变化的分岔图和对应的Lyapunov指数谱图Fig.3 Bifurcation diagram and Lyapunov exponents spectrum of the system with parameter a
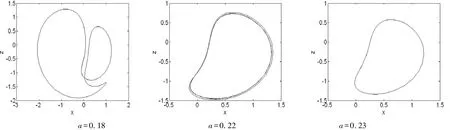
图4 系统在x-z平面的典型周期相图Fig.4 Typical cycle phase portraits of system in x-z plane
图5给出了固定参数a=0.11,系统随参数b∈[0.1,0.3]变化关于x的分岔图和Lyapunov指数谱图,几个典型参数下的周期轨如图6所示.由这些图可见系统随参数变化表现出丰富的动力学行为,在混沌区域也有几处出现较窄的周期窗口.
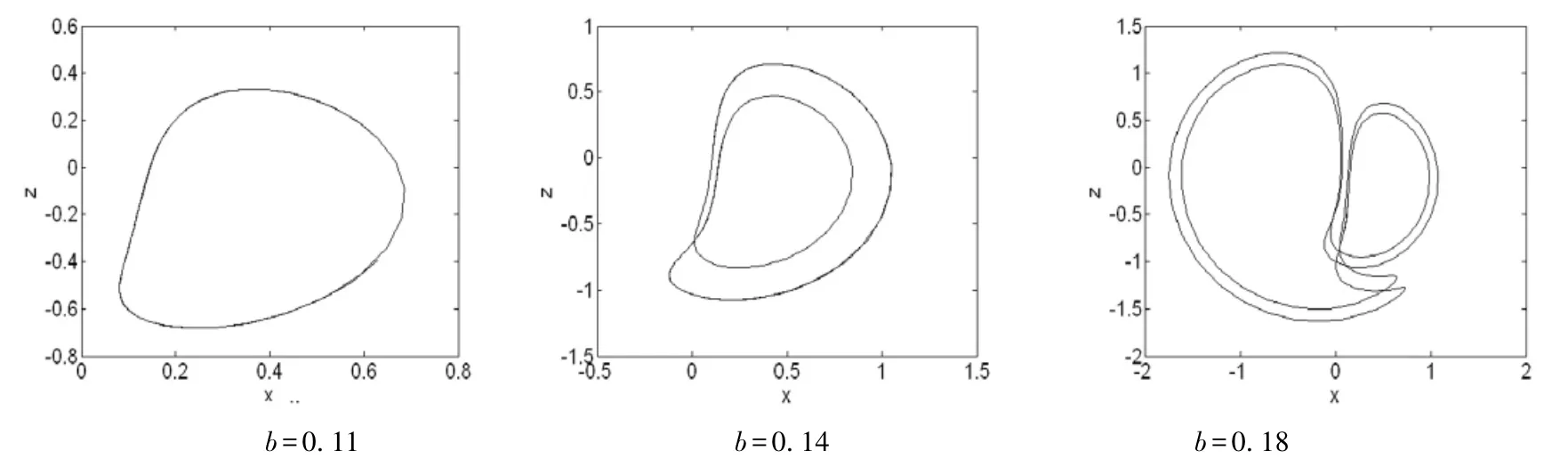
图6 系统在x-z平面的典型周期相图Fig.6 Typical cycle phase portraits of system in x-zplane
2.4 拓扑等价性
由于本文构造的新混沌系统的混沌吸引子比较独特,与Lorenz吸引子形状完全不同,与Chen系统、Lü系统也不同,它们均有3个平衡点,而这个新系统只有2个平衡点,所以该新混沌系统与这3个混沌系统之间均不存在同胚变换,因此是一个新型的混沌系统.
[1] Lorenz E N.Deterministic nonpefiodic flow[J].At Mos Sci,1963,20(2):130-141.
[2] Chen G,Ueta T.Yet another chaotic attractor[J].International Journal of Bifurcation and Chaos,1999,9(7):1465-1466.
[3] Lü J.Chen G R.A new chaotic attractor cioned[J].International Journal of Bifurcation and Chaos,2002,12(3):659-661.
[4] Lü J,Chen G,Cheng D S.Celikovsky.Bridge the gap between the Lorenz system and the Chen system[J].International Journal of Bifurcation and Chaos,2002,12(12):2917-2926.
[5] 高智中.一个新混沌系统[J].湖南文理学院学报,2011,23(1):34-37.
[6] 狄崇利,黄东卫,蔡为民.一类非线性系统的混沌特征分析[J].天津师范大学学报,2010,30(2):1-5.
[7] 王杰智,陈增强,袁著祉.一个新的混沌系统及其性质研究[J].物理学报,2006,55(8):3956-3963.
[8] 高智中.一个新自治混沌系统的动力学分析[J].数值计算与计算机应用,2012,33(1):1-8.
[9] 韩春艳,薛华,吴新华.一个新的混沌模型及其数字伪随机信号的实现[J].河北师范大学学报,2010,34(2):165-169.
[10] 张建雄,唐万生,徐勇.一个新的三维混沌系统[J].物理学报,2008,57(11):6799-6809.

