宇宙学表观视界的霍金辐射和热力学

刘显明

(湖北民族学院理学院，湖北恩施445000)

黑洞物理涉及了引力理论、量子理论和热力学理论，是理论物理学和天文学研究的一个热门研究领域.黑洞物理研究进展中的一个重大发现是20世纪70年代Hawking利用弯曲时空量子场论的方法发现物质塌缩形成的黑洞能够产生热辐射［1］.人们由此意识到Bekenstein发现的黑洞力学四定律［2］就是黑洞的热力学四定律.在这里，黑洞视界的面积、表面引力分别被看作为黑洞的熵和温度.黑洞热力学的建立带来了信息疑难等让人深思未解的疑问，同时也暗示了量子理论、引力理论和热力学之间存在着深刻的内在联系.

关于Hawking辐射的计算，除了Hawking的原始推导方法之外，还有Damour－ruffini法［3］，Hamilton－jacobi方法［4］等.目前，流行的一种方法是Parikh和Wilczek引入的研究黑洞Hawking辐射的量子隧穿法［5］.此研究方法可类比于量子力学中的正负电子对的产生过程.Hawking辐射的现象被描述成视界面附近的正负能粒子对的产生.一个带负能的虚粒子产生后落入了黑洞，同时一个带正能的实粒子产生于视界外.这可以等效看做一个带正能的实粒子从黑洞里面穿过视界.视界在这里被看作为粒子隧穿的势垒.处于无穷远渐近平直区域的观测者可以观测到Hawking辐射.结合能量守恒定律并考虑到辐射过程中的反作用，Hawking辐射被发现不再是纯热辐射，由此可以用来部分解释信息疑难问题.随后这一工作被推广于研究更加一般的Kerr－newman 黑洞［6－8］.鉴于在隧穿法中对能量守恒定律和辐射反作用的考虑，刘文彪教授等［9－10］用Damour－ruffini法研究了更加一般黑洞的Hawking辐射，得到了非纯热谱，部分解释了信息疑难问题.文献［11］，把这一工作进一步推广到研究宇宙黑弦的Hawking辐射.

近年来，人们利用半经典的量子隧穿法探讨了动态黑洞的Hawking辐射.一个物理上的黑洞一般不应该是稳态的，而是动态的，因此动态黑洞的研究更具有现实意义.然而由于一个动态黑洞不再存在类时的Killing矢量场，一般具有事件视界和表观视界，问题变得比较复杂.一方面，Roberto Balbinot［12］，赵峥［13］，Vagenas［14］等讨论了动态黑洞事件视界上的Hawking辐射.赵峥教授把稳态时空中事件视界的整体性和类光性推广于动态时空建立动态黑洞中的事件视界的概念，从而利用Damour－ruffini法证明了事件视界上存在Hawking辐射.他们的结论表明在动态黑洞中可以同样引入Hawking温度、熵的概念，但是得不到一套完美的热力学第一定律.这一工作仍在继续的探索之中［15］;另一方面，研究者对动态黑洞产生了浓厚的兴趣［16］.Hayward［17－19］，Ashtekar［20］以及 Booth 等人先后定义了 Trapping horizons、isolated horizons 、dynamiacal horizons以及slowly evolving horizons.这些视界和熟知的事件视界(event horizons)一样都是3维子流行.不同的是他们更多依赖于局域的特征.在 Hayward［17－19］、Alex B.Nielsen［21］和 Hiscock 等人的研究中指出可以在这些动态的视界上计算Hawking辐射、定义面积熵并且建立热力学定律.最近，半经典的Hamilton－jacobi方法已经被推广用于研究动态黑洞的Hawking辐射［22］.同时，在文献［23－27］中，利用半经典半量子的Hawking辐射的推导方法，仔细的研究了动态黑洞表观视界上的Hawking辐射和热力学.我们的结论表明在表观视界上确实存在热辐射，并且可以建立热力学第一定律.

目前，大量的天文观测数据表明一种未知的暗能量正在驱使宇宙经历一个加速膨胀的阶段［28］.在标准模型中，均匀各向同性的膨胀宇宙可以由Friedmann－robertson－walker(FRW)度规来描述.研究FRW宇宙学时空的量子引力效应对宇宙学和黑洞物理学的发展都具有特殊的意义.因为FRW度规描述的是一个动态的时空，所以在本文中将利用两种动态的乌龟坐标变换，应用Damour－ruffini方法计算FRW宇宙学表观视界的霍金温度，并研究其热力学.

1 Friedmann－robertson－walker时空度规

宇宙学原理要求每一时刻的宇宙空间在宇观尺度下是均匀各向同性的.满足这样要求的时空常用Friedmann－robertson－walker(FRW)度规描述:

其中:a(t)是尺度因子，dΩ2=dθ2+sin2θdφ2表示一个两维的球面 S2，k=±1，0分别对应于空间曲率为正、负以及平直的时空几何.在本文中为了简化计算，仅仅讨论平直时空几何(k=0).

度规(1)可以改写为:

其中:R=ar，x0=t，x1=r，两维的度规 hab=diag(－1，a2/(1－kr2)).在 FRW 宇宙中的表观视界 RA满足:

hab∂aR∂bR=0

经过简单的计算，可以得到平直时空几何情况下表观视界为:RA=1/H.其中:于是利用坐标变换R=ar，线元(2)变成为一个类Painlevé－gulstrand坐标的形式:

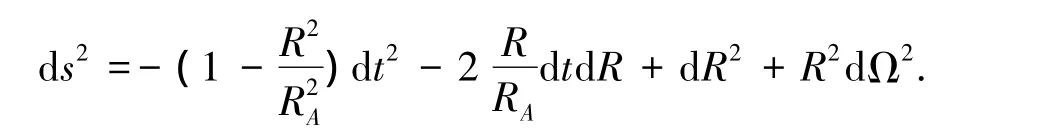
利用量纲约化技术，近表观视界的等效二维度规为:

类光测地线可以通过计算而得到为:

其中±分别与出射光和入射光相对应.

作变分可以得到无质量粒子的Klein－gordon方程为

代入线元(3)，可得在FRW宇宙学时空中表观视界面附近的无质量粒子的Klein－gordon方程:

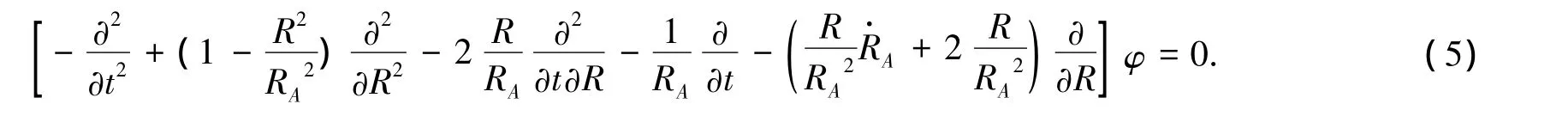
2 瞬时动态乌龟坐标变换和霍金温度

在文献［13］中赵峥教授等第一次应用一个动态的乌龟坐标变换去研究动态黑洞的霍金辐射.这种动态乌龟坐标变换依赖于某一个特定的时刻v0，把它称之为“瞬时”动态乌龟坐标变换.在FRW时空，“瞬时”动态乌龟坐标变换可以设定为:

式中κ t0()为一个待定参数，在乌龟坐标变换下是一个常数，从方程(1)可得:

把方程(11)用于方程(10)，并利用条件(12)，则方程(10)可写成:

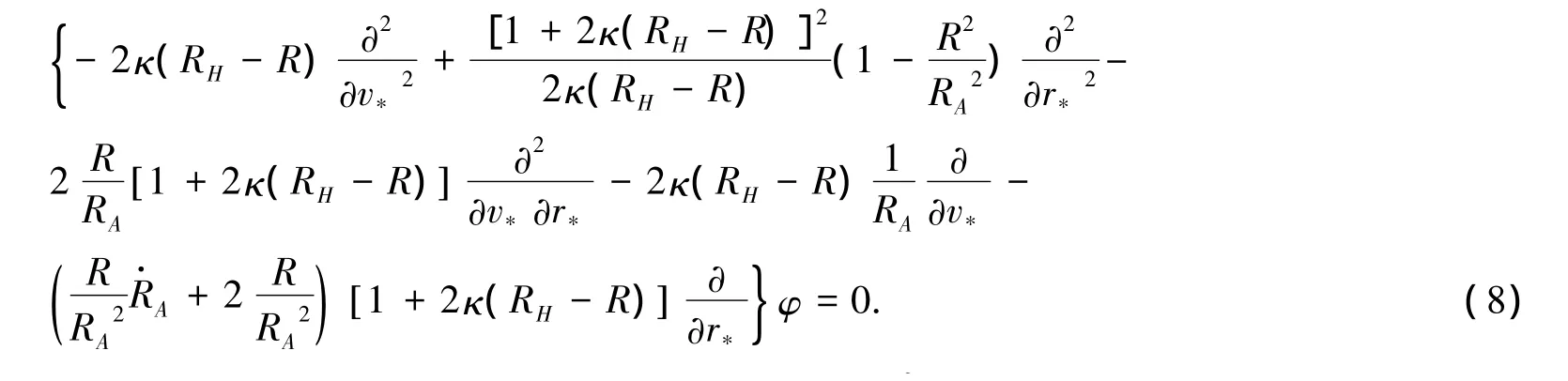
可以假设在位置R=RH处方程(8)可以化为标准的波动方程.当的系数在R=RH处为有限值时则要求RH=RA，所以下面讨论将在表观视界附近讨论，粒子的霍金辐射谱也正好是可以看作来源于表观视界的位置.等进一步，当，可以确定所以方程(8)在表观视界处可以化成标准的波动方程的形式:

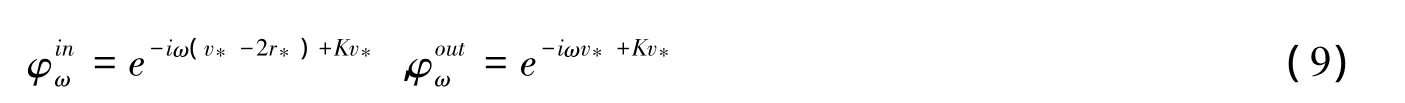
方程(9)分别描述入射波和出射波.由于在FRW宇宙中观者是出于表观视界内的，所以下面的讨论都仅仅关注入射波的情况.

于是可以根据Damour－sannan的工作［3］可以得到入射波的辐射率为

对应的辐射谱为:

式中±分别对应为费米子和波色子，TAH为辐射温度

显然可见式(10)为黑体辐射谱，对应的温度TAH可以理解为在FRW表观视界的霍金温度.此结论与文献［28－29］用隧穿法求出的结果是一致的.

3 推广的动态乌龟坐标变换和霍金温度

用类似文献［23－27］中的工作，引入一个推广了的动态乌龟坐标变换来研究FRW宇宙时空表观视界上的霍金辐射.

动态的乌龟坐标变换可以取为:

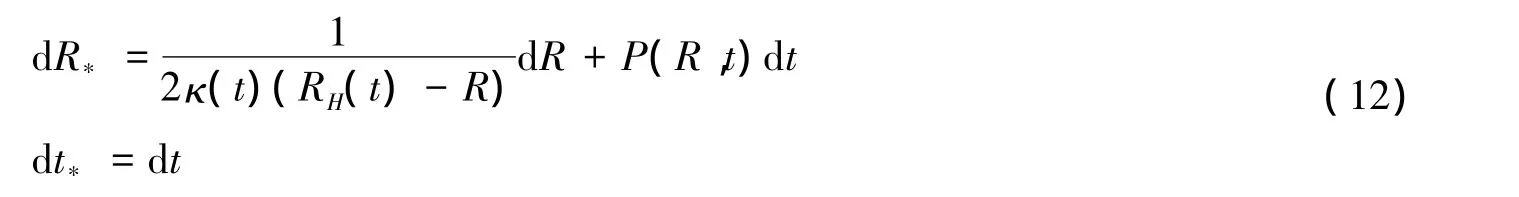
可以验证这里引入的乌龟坐标变换满足文献［23－27］中提出的一般的动态乌龟坐标变换的条件:

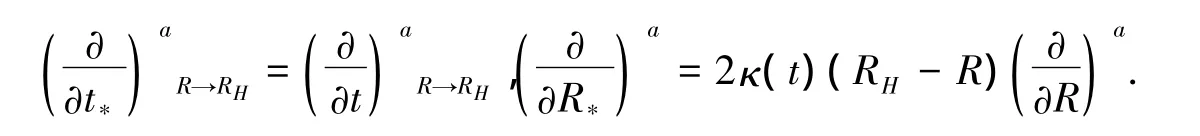
利用坐标变换(12)，可以得到:

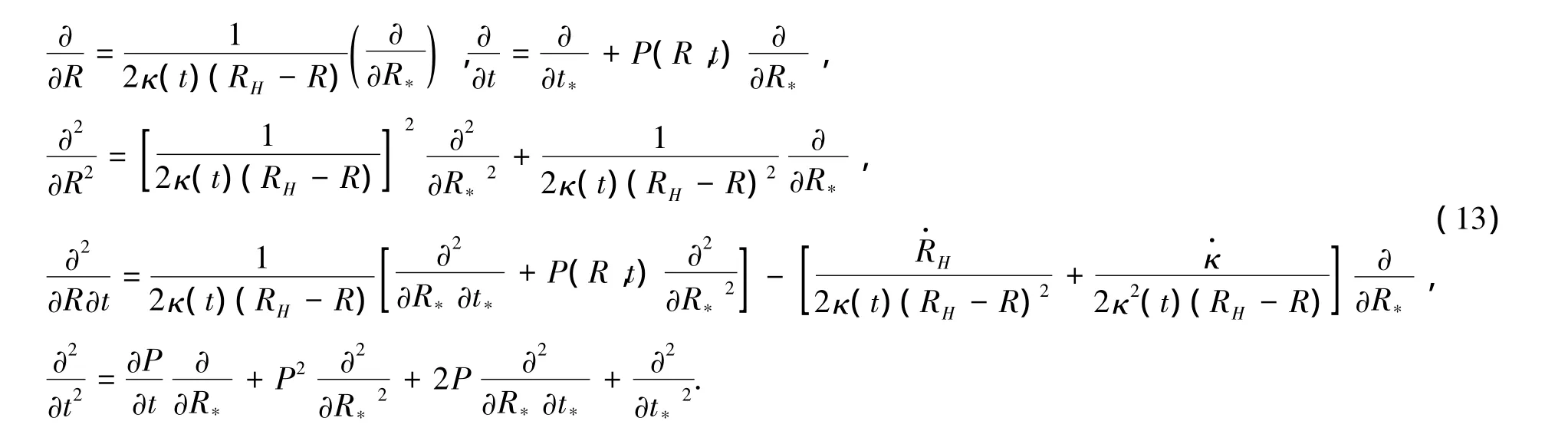
现在把方程(12)代入方程(18)，并利用方程(13)，则Klein－gordon方程可整理为:

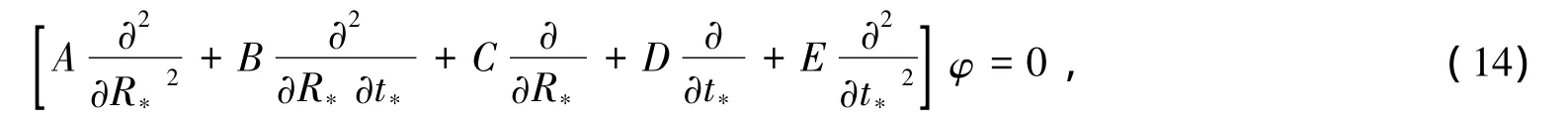
依据文献［23－27］，可以假定方程(14)在视界处化为标准的波动方程.利用，发现系数A在视界附近有限必须要求RH=RA.此条要求说明下面的讨论需要限定在表观视界处讨论，同时也说明FRW宇宙学时空的霍金辐射可以出自于表观视界.如果进一步要求在视界处系数A=1，可以得到类似文献［23－27］，现在要求入射的粒子沿着径向类光测地线进入表观视界内，于是利用方程(4)，可得:

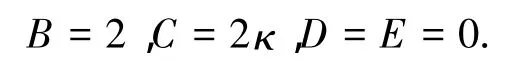
所以，方程(14)能够在表观视界附近处化简为标准的波动方程形式:对应方程的两个线性独立的解为:

其中:L(t*)为的t*函数，记为，这两个解分别代表入射波和出射波.因为在FRW时空中观者在视界之内，所以我们仅考虑来源于视界外的入射波.进一步考虑到方程(12)和类光条件(15)，可以得到动态乌龟坐标的变换的形式为:

把方程(17)带入方程(16)，可以得到入射波函数为:

注意到方程(18)只能描述视界内的入射波，于是利用解析延拓的方法，入射波在视界内外的函数形式可以分别表述为:

于是，利用Damour－sannan的工作［3］，可得入射粒子的辐射率为:

以及对应的霍金温度为:

此结果与在第2节中计算得到的表观视界的霍金温度(11)是一致的.

4 表观视界的热力学

根据球对称时空中Misner－sharp(MS)质量的定义，可以得到在平直的FRW时空的表观视界的MS质量为:MAH=RA/2.

下面假定Bekenstein的面积熵假设对于表观视界仍然成立，可以得到对应于FRW时空表观视界的熵为:

其中AAH为表观视界的面积.因此根据方程(11)或者方程(19)～(21)，可以得到适用于表观视界的热力学第一定律的形式:

在前面的讨论之中，没有讨论时空之中是否有物质，仅仅关注了时空几何部分的能量转化关系.下面将考虑时空中具有物质，并假定物质可以视为理想流体.在FRW宇宙学时空中，流体的压强和密度满足Friedmann方程:

和连续性方程:

方程(22)和方程(23)中的ρ和p分别表示理想流体的密度和压强.

此时宇宙时空总的能量E将要包含几何部分和物质部分，可以改写为:

于是根据方程(22)和方程(24)，可以得到:

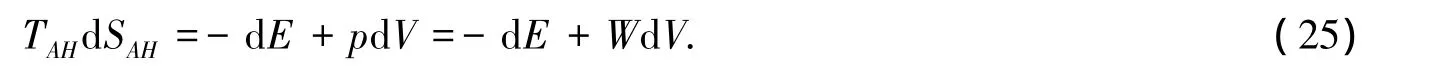
方程(25)可以视为FRW宇宙学表观视界的热力学第一定律的形式.

5 结论

本文利用Damour－ruffini方法研究了FRW宇宙学表观视界的霍金辐射，得到了对应的霍金温度，同时利用Bekenstein－hawking熵和MS质量，在表观视界上建立了对应的热力学第一定律.文中结论证实在文献［23－27］中引入的动态乌龟坐标变换适用于研究FRW宇宙学表观视界的霍金辐射.

动态黑洞的霍金辐射和热力学研究有助于进一步探索引力理论、量子理论和热力学之间的内在联系.在进一步的工作中将会注意以下几个问题:

1)本文结论仅仅适用于视界变化很慢的近平衡情况，对于更一般的复杂情况需要应用非平衡物理的相关知识进一步深入的讨论.

2)动态黑洞时空中的质量以及表观视界的表面引力的定义值得进一步深入的探讨.

3)动态视界中热力学定律中功密度的定义值得进一步商榷.

［1］ Hawking S W.Particle creation by black holes［J］.Comm Math Phys，1975，43(3):199－220.

［2］ Bekenstein Jacob D.Black Holes and Entropy［J］.Phys Rev D，1973，7:2333－2346.

［3］ Damour T，Ruffin R.Black－hole evaporation in the Klein－Sauter－Heisenberg－Euler formalism［J］.Physical Review D，1976，14(2):870－892.

［4］ Srinivasan K，Padmanabhan T.Particle production and complex path analysis［J］.Phys Rev D，1999，60:024007.

［5］ Parikh M K，Wilczek F.Hawking radiation as tunneling［J］.Phys Rev Lett，2000，85:5042－5045.

［6］ Zhang J Y，Zhao Z.New coordinates for Kerr－Newman black hole radiation［J］.Phys Lett B，2005，618(1/4):14－22.

［7］ Jiang Q Q，Wu S Q，Cai X.Hawking radiation as tunneling from the Kerr and Kerr－Newman black holes［J］.Phys Rev D，2006，73:064003.

［8］ Jiang Q Q，Wu S Q，Cai X.Hawking radiation from dilatonic black holes via anomalies［J］.Phys Rev D，2007，75:064029.

［9］ Xiaokai He，Wenbiao Liu.Modified Hawking radiation in a BTZ black hole using Damour－Ruffini method［J］.Physics Letters B，2007，653(2/4):330－337.

［10］ Zhou Shiwei，Liu Wenbiao.Charged Dirac particles'Hawking radiation from a Kerr－Newman black hole［J］.Phys Rev D，2008，77(10):104021.

［11］ Liu Xianming，Liu Wenbiao.Corrected Hawking radiation from a charged rotating black string［J］.Astrophys Space Sci，2008，318(3/4):219－223.

［12］ Babinot R，Barletta A.The backreaction and the evolution of quantum black hole［J］.Class Quantum Grav，1989，6:195－198.

［13］ Zhao Z，Dai X.Hawking Radiation from a Non－static Black Hole［J］.Chin Phys Lett，1991，8:548.

［14］ Vagenas Elias C，Das Saurya.Gravitational anomalies，Hawking radiation，and spherically symmetric black holes［J］.JHEP，2006，0610:025.

［15］ Yang Jian，Zhao Zheng，Liu Wenbiao.Tortoise coordinate and Hawking effect in a dynamical Kerr black hole［J］.Astrophysics and Space Science，2011，331:627－632.

［16］ Gourgoulhon Eric，Jaramillo Josephine Luis.New theoretical approaches to black holes［J］.New Astronomy Reviews，2008，51:791－796.

［17］ Hayward S A.General laws of black－hole dynamics［J］.Phys Rev D，1994，49:6467－6474.

［18］ Hayward S A.Energy Conservation for Dynamical Black Holes［J］.Phys Rev Lett，2004，93:251101.

［19］ Hayward S A.Energy and entropy conservation for dynamical black holes［J］.Phys Rev D，2004，70:104027.

［20］ Ashtekar A，Krishman B.Dynamical horizons and their properties［J］.Phys Rev D，2003，68:104030.

［21］ Nielsen Alex B.Black holes and black hole thermodynamics without event horizons［J］.Gen Rel Grav，2009，41:1539－1584，

［22］ Criscienzo R D.Hamilton－Jacobi tunneling method for dynamical horizons in different coordinate gauges［J］.Class Quantum Grav，2010，27:015006.

［23］ Liu X，Liu W.Where Does Hawking Radiation of a Dynamical Black Hole Come from［J］.Int J Theor Phys，2010，49:1088－1095.

［24］ Zhou Shiwei，Liu Wenbiao.Apparent horizon and event horizon of a Vaidya black hole［J］.Modern Physics Letters A，2009，24(26):2099－2103.

［25］ Niu Zhenfeng，Liu Wenbiao.Hawking radiation and thermodynamics of a Vaidya－Bonner black hole［J］.Research in Astronomy and Astrophysics，2010，10(1):33－38.

［26］ Liu Xianming，Liu Wenbiao.Apparent horizon and event horizon thermodynamics of a Vaidya black hole using Damour－Ruffini method［J］.Astrophysics and Space Science，2011，331:237－244.

［27］ Liu Xianming.General Tortoise Coordinate Transformation in a Dynamical Kerr－Newman Black Hole［J］.Int J Theor Phys，2012，51:518－524.

［28］ Perlmutter S.Measurements of omega and lambda from 42 high－redshift supernovae［J］.Astrophys J 1999，517:565－572.

［29］ Cai Rong－Gen，Cao Li－Ming，Hu Ya－Peng.Hawking radiation of an apparent horizon in a FRW universe［J］.Class Quant Grav，2009，26:155018.

［30］ Misner C M，Sharp D H.Relativistic Equations for Adiabatic，Spherically Symmetric Gravitational Collapse［J］.Phys Rev，1964，136:B571－B576.

［31］ Gong Yungui，Wang Anzhong.The Friedmann equations and thermodynamics of apparent horizons［J］.Phys Rev Lett，2007，99:211301.