复杂装配尺寸链的图论法求解研究

张 亚，冯 刚

ZHANG Ya1,2,FENG Gang1

(1.浙江工业职业技术学院，绍兴 312000；2.浙江大学 机械工程学系，杭州 310027)

0 引言

图论是一个新兴的数学分支,目前在物理学、化学、运筹学、计算机科学、信息论、网络理论以及经济管理等许多领域都得到广泛的应用[1]。在机械装配领域也越来越受到人们的重视[2]。

一般情况下，我们可以利用尺寸链的原理,通过解装配尺寸链求出各装配尺寸。 尺寸链分析是保证机器装配质量的重要方法[3]。然而在机械部件的装配中，如果装配的部件较多、尺寸关系复杂，尺寸链的表示和求解将很困难、繁琐，容易出错。本文根据装配尺寸的图论表示模型,提出了装配尺寸链的矩阵求解方法。此方法可以用一个矩阵式表示出所有的尺寸关系并一次求解出所有封闭环的尺寸，提高了尺寸链求解的效率，为复杂尺寸链的求解提供了有效的方法。下面将以图1所示滚轮部件的装配为例，说明基于图论的装配尺寸链求解方法。

1 装配尺寸链的图论模型

图1[4]所示滚轮部件由六个零件组成，零件的设计尺寸为：L1=15mm,L2=38mm,L3=50mm,L4= 80mm,L5=80.2mm,L6=10mm,L7=15mm,L8=40mm以及L9=0，部件的尺寸与公差模型见图2。现在要求根据零件的设计尺寸求解三个装配尺寸（即封闭环尺寸）：__

滚轮3和框架1之间的间隙X_N1；机架1与螺母6的间隙XN2；机架1大孔 的轴线与滚轮3中垂直于轴线的两个端面之间的中间平面之间的距离为XN3。

我们首先给出装配尺寸链的图论模型。

图1可以定义为二元组G=〈V（G），E（G）〉

1）V（G）是非空的集合V（G）= {v1, v2, ...,vn}，元素vi（i = 1, 2, ..., n）表示图G的结点，即零件的装配特征。本图中只包含与装配尺寸和设计尺寸相关的结点。V（G）称为图G的结点集合，简记为V。

2）E（G）是V中结点的有序偶组成的集合，E（G）= {e1, e2, ..., em} = {vivj, i＜j，i, j∈1, 2, ...,n}。边ek与有序偶〈vivj〉相关联，为有向边，其中vi称为ek的起始结点，vj称为ek的终止结点。本文中，为了判断组成环的传递系数，指定组成环（设计尺寸）的方向为从左侧的节点指向右侧的结点，故规定i＜j。图2所示即滚轮装配的图论模型，图中的粗实线表示装配尺寸即封闭环。

2 装配尺寸链的求解

建立装配尺寸链矩阵式的步骤如下：首先，

利用图论模型中的结点信息求出各组成环的传递系数，然后根据传递系数和边的权值信息建立装配尺寸的矩阵式，求解得到装配尺寸。

2.1 根据结点信息在图中判断增减环，确定组成环的传递系数

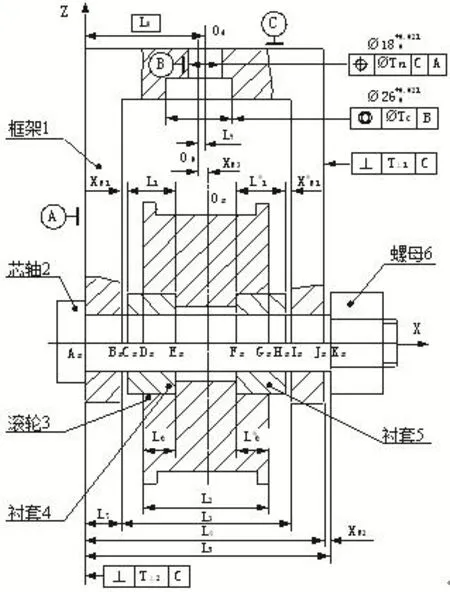
图1 滚轮部件装配图

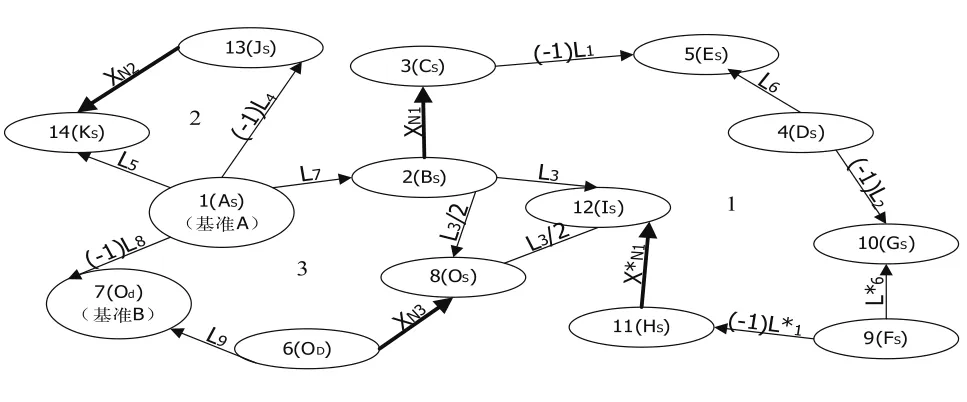
图2 装配尺寸的图论模型

传递系数是表示各组成环对封闭环影响大小的系数。尺寸链中封闭环与各组成环的关系可表示为:L0=f(L1,L2,…,Lm)。设第i个组成环的传递系数为ξi，则ξi＝对于增环，，ξi为正值；对于减环，ξi为负值[1]。在直线尺寸链中，增环的传递系数为+1，减环的传递系数为-1。

组成环或封闭环在图论模型中的有顺时针或逆时针两个相反的方向。本文提出一种在图论模型中求解组成环传递系数的方法，即：与封闭环（装配尺寸）反向的组成环（零件设计尺寸）为增环，传递系数ξij＝+1；与封闭环（装配尺寸）同向的组成环（零件设计尺寸）为减环，ξij＝-1。

图2中有3个包含封闭环的圆环。由L3、L3/2、L3/2组成的圆环没有包含封闭环，未涉及装配关系，故不予考虑。封闭环XN1、XN2、XN3所在的环分别用序号1、2、3标识。各结点对应的特征在装配图中按从左至右的顺序依次为:AS、BS、CS、DS、ES、OD、Od、OS、FS、GS、HS、IS、JS、 KS，为显明起见，依次用1、2、3…14来表示。按照上述方法判断得到的传递系数的值已在图上标出。

2.2 装配尺寸链的矩阵表示与求解

封闭环的基本尺寸等于各增环的基本尺寸之和减去各减环的基本尺寸之和：

对于包含多个封闭环（装配尺寸）的装配尺寸链，我们可以建立其矩阵式如下：

如果一个装配尺寸图论模型包含i个包含封闭环（装配尺寸）的环，设计尺寸为L1～Lj,装配尺寸为XN1～XNi,则有：

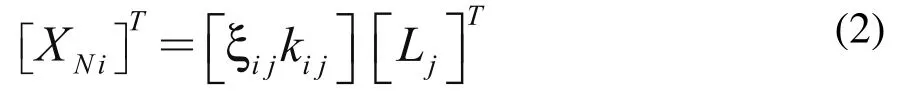
kij为组成环尺寸的比例系数，如对于组成环L3/2， k13＝1/2;

尺寸与设计尺寸之间的线性关系。

本例中， 封闭环的序号i=1，2，3；组成环的序号j=1，2，…,9。

因为X*N1=XN1, 环1中的封闭环相当于2XN1。为了能以XN1作封闭环，各组成环的kij值均需除以2。又因为L*6= L6,L*1= L1, 故k11=1,k12=1/2,k13=1/2,k16=1。

所以尺寸链系数矩阵为：

所以，装配尺寸链矩阵方程为：

本文用mathematica5.0进行矩阵运算。使用主菜单命令“input”下的“creat table/matrix/palette”命令直接输入矩阵。如对于尺寸链系数矩阵，设置矩阵行数与列数分别为i和j，产生一个空白矩阵i×j，然后将 的值依次输入，即可得到尺寸链系数矩阵。矩阵相乘用如下命令：X=KL。求得装配尺寸链的封闭环列向量为：

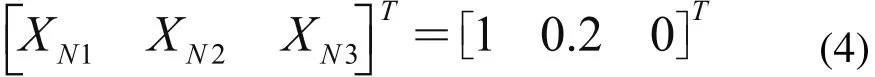
所以，此滚轮部件的装配尺寸为：滚轮3和框架1之间的间隙XN1等于1；机架1与螺母6的间隙XN2等于0.2；机架1大孔 的轴线与滚轮3中垂直于轴线的两个端面之间的中间平面之间的距离XN3等于0，即要求两者共面。

3 结束语

在工程机械的装配中，如果装配的部件较多、尺寸关系复杂，尺寸链的表示和求解将很困难、繁琐，容易出错，甚至无法用通常的尺寸链方法求解装配尺寸。本文根据装配尺寸链的图论模型，建立了装配尺寸链的矩阵式，并提出一种在图论模型中判断尺寸链传递系数的新方法，使得复杂装配尺寸链可以很容易地求解出来并避免差错。通过滚轮部件的装配实例，验证了本文所提出方法的有效性。

[1] 尹成龙.图论法查找和解算工艺尺寸链的研究[J],安徽农业大学学报,1998,25(2):203-205.

[2] 季忠齐,童若锋,林兰芬,蔡铭,董金祥.基于图论和启发式搜索的装配序列规划算法[J],计算机工程,2003,13:115-117.

[3] 徐振高,蒋向前.互换性与测量技术[M],北京:高等教育出版社,2004.

[4] 黄美发,钟艳如,CAD系统中并行公差的建模方法[J],中国机械工程,18:1623-1626.