基于模糊时间并具有成组约束的车间排序算法

黄锦钿，陈庆新，毛 宁

HUANG Jin-dian1, CHEN Qing-xin2, MAO Ning2

（1.揭阳职业技术学院，揭阳 522000；2.广东工业大学，广州 510006）

0 引言

单元成组加工是现代制造企业应用广泛的一种生产作业方式，该生产方式是将加工工艺相似的工件放到一组，并根据工件的工艺要求为所需要的设备分组，运用单元成组加工有利于保证工件加工质量和提高生产效率。文献[1]认为模具型腔的加工受到EDM车间工艺条件的限制，加工型腔所用的电极必须被成组安排到同一台设备，从而研究了后工序带有成组特征的模具电极调度策略，并在不同的加工条件下提出相应的调度算法。文献[2]在假定工件具有精确的加工时间和到达时间前提下，提出了一种前工序具有成组约束的两阶段柔性同序加工车间排序算法。在企业的实际生产中，往往存在大量的不确定因素，如机器故障、操作工人的熟练程度、环境参数等的影响，很少能获得精确的加工时间和到达时间。因此，本文将在文献[2]已有研究的基础上，借助模糊数学理论[3,4]，将工件的加工时间和到达时间作模糊数考虑，在前工序带成组加工约束的两阶段柔性同序加工车间中，基于遗传算法提出一种新的启发式算法，调度目标是为所有工件指定加工设备并确定加工顺序，使所有工件经过这两道工序的最大完成时间最短。现结合模具企业生产的实际情况，将问题进一步具体化，并提出以下假设。

假设1：各部件到达车间的时间已知但不确定，不同部件到达车间的时间不一定相同，同一部件中的工件到达车间的时间相同；

假设2：每个部件包括多个工件，且数量确定已知；

假设3：每个工件都必须经过两道工序的加工，而且加工顺序不能改变；

假设4：允许工件在工序之间等待，两道工序之间具有无限的缓存能力；

假设5：每道工序对应的工作中心都由若干个工作小组组成，每个工作小组中有若干台设备，各工作小组的设备数量不等且确定已知，相同工作小组中的设备工作效率相同，不同工作小组中的设备工作效率不同；

假设6：工件在各工序各工作小组需要的加工时间已知但不确定，相同部件中的工件加工要求相同，不同部件中的工件加工要求不同；

假设7：一台设备在同一时刻只能加工一个工件；

假设8：工件一旦在设备上开始加工，不允许中途停下来，插入其他的工件；

假设9：在前工序，同一部件中的工件必须被安排在同一工作小组加工。

1 模糊时间

1.1 模糊处理

模糊数是模糊集的一种特殊形式。模糊数一般采用分段直线的方法来表示，最常用的就是三角形模糊数和梯形模糊数，其对应的隶属度函数就是三角形和梯形。本文中工件的到达时间采用三角模糊数 来表示，其隶属度函数公式如(1)所示：

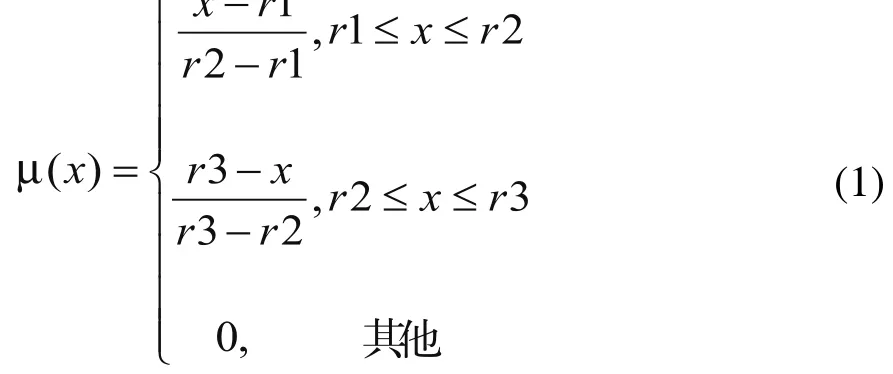
在模具企业的实际生产中，有经验的调度员在估计某一工件的加工时间时，一般认为工件的加工时间在某一个时间区间段内都是合理的，如果低于这个时间段的下界或高于它的上界时，随着偏离的距离越远则其合理性就越低，即满意度越低。因此，工件的加工时间采用梯形模糊数来表示，其隶属度函数如式(2)所示：

在模糊调度问题中，模糊数的求和及取大操作是关键，求和操作用于计算工件的模糊完工时间，取大操作用于确定工件工序的开工时间。由于本文中工件的到达时间和加工时间分别采用三角模糊数和梯形模糊数，因此在求和计算工件模糊完成时间时存在两种模糊数间的三种不同运算，根据模糊数扩张原理，模糊数的求和运算作如下三个定义。

和计算工件的完成时间一样，在确定工件的开工时间时同样存在三种不同的取大运算，根据模糊取大操作的原理作如下三个定义。

定义6：如果三角模糊数和梯形模糊数作取大运算，设则将三角模糊数表示为梯形模糊数的特殊形式，即三角模糊数表示为 ，因此

1.2 排序方法的选用

模糊数的比较是模糊优化的一个关键问题，要使得两个模糊数之间的比较有意义必须在相同模糊度的情况下进行，虽然很多学者都在研究模糊数的比较方法，提出了各种比较指标。但是，迄今为止还没有一个方法被公认为是最好的，所有的方法在复杂的情况下都或多或少地缺乏分辨力，甚至与人们的直觉相抵触。实际应用中，具体采用哪种方法则主要取决于问题的本身和决策者的态度。由于本文研究的调度问题比较复杂，且在实际生产中调度人员的估计方法也是采用取均值的方式，所以本文采用均匀分布的Lee-Li法，把相关的模糊数转化为精确值来处理。

将模糊集 的均值和标准偏差分别记为m()和σ()，借助模糊事件概率测度的概念，均匀分布的Lee-Li法用下式计算均值和标准偏差：

在模糊均值和模糊偏差的基础上，Lee-Li进一步定义了模糊集综合评判排序指标如下：

这里的β是由决策者选定的权值，它反映了均值与偏差在决策者心目中的相对重要程度,通过式(5)我们可以把模糊数转化为精确值，以此为基础得到目标函数值。

2 基于遗传算法的求解过程

2.1 遗传算法概述

遗传算法自从1975 年由Holland 提出至今已被广泛的应用到组合优化、机器学习、模式识别以及人工神经元网络等方面[5,6]。遗传算法基本流程描述如图1所示：

图1 遗传算法流程图

2.2 编码设计

根据本文调度问题的特点，相同部件中的工件在前工序中必须被安排到同一个加工小组加工，因此在编码时将相同部件中的所有工件看成一个整体，同时将前工序中同一个加工小组中的机床看成一个整体。

编码时，用自然数序列代表所有可能的部件加工顺序，而不同加工小组上的部件则用‘0’隔开。对于n个部件、前阶段有M个工作小组的问题，一个合法的染色体应包括n个部件符号，（M-1）个间隔符号‘0’，总长度为（n+M-1）个基因。现假设有7个部件、前工序有3个工作小组的情况，则染色体的基因编码表示应为：[1 6 3 0 7 4 0 2 5]。则各小组上对应的部件加工顺序为：M1：1→6→3；M2：7→4；M3：2→5。

从染色体的编码信息中可以确定部件在前工序中的加工小组和加工顺序，然后对比部件的到达时间和机床的空闲时间，进一步确定工件对应的机床和加工顺序。这种编码方式有利于保证满足工件成组加工的约束，而且有利于提高搜索效率。

2.3 适应度函数设计

本文调度的目标函数值是最短的最大完成时间f(S)。按先到达先加工的原则确定工件的加工顺序，所有工件通过两道工序的最大完成时间为Cmax，现通过下面公式将目标函数值转化为适应度函数值F(S)：

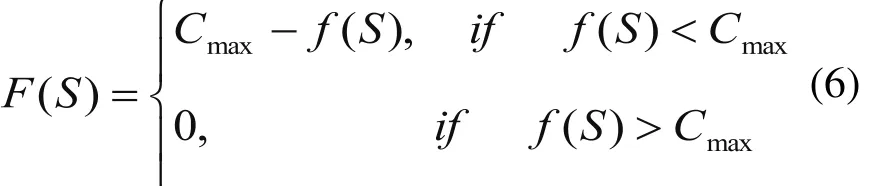
通过式（6）计算转换，使得目标函数值较小的染色体有较高的适应度，而且各染色体将以适当的概率遗传到下一代。

2.4 初始种群设计

为了使初始种群尽可能多样化并且提高寻优效率，本文采用两种方式产生初始种群。第一种方式是采用完全随机方法产生初始种群，例如有n个待排产的部件，前工序中有M个加工小组，则首先产生由自然数1到n组成的随机序列，然后将M-1个0随机插入到序列中，这样就得到一个长度为n+M-1的染色体，反复做上述操作，可以得到若干个随机初始染色体；第二种方式是采用确定方式产生优良初始染色体，采用先到达先加工的原则可以得到一个适应度较高的初始染色体。将这两种方式产生的染色体结合到一起作为初始种群，这样不仅增加了种群的多样性，而且提高了种群的进化进程。

2.5 选择算子

选择过程是为了从当前的群体中选出优良的个体，使他们有机会作为父代将其优良的个体信息传递给下一代，本文采用确定式采样选择方法来选择优良的个体。具体操作步骤如下：

1）计算群体中各个个体在下一代群体中的期望生存数目Ni：

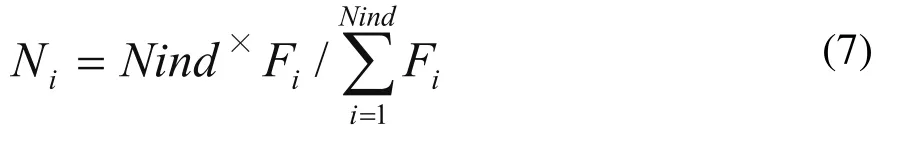
式中，Nind为种群个_体数_量，i = 1,2,3,…,Nind。

2）用Ni的整数部分确定各个对应个体在下一代群体中的生存数目。其中表示取不大于x的最大的整数。此时可确定出下一代群体中的个个体。

3）按照Ni的小数部分对个体进行降序排序，顺序取前Nind-个个体加入到下一代群体中。至此可完全确定出下一代群体中的Nind个个体。

这种选择操作方法可保证适应度较大的一些优良个体一定能够被保留在下一代群体中，并且操作也比较简单。

2.6 交叉算子

交叉运算是指对两个相互配对的染色体按某种方式相互交换其部分基因，从而形成两个新的个体，它在遗传算法中起着关键作用。在交叉运算之前必须对群体中的个体进行配对，本文采用随机配对的配对策_略，即将_群体中的Nind个个体以随机的方式组成 对配对个体组，交叉操作是在这些配对个体组中的两个个体之间进行的。本文每个染色体编码包含前工序中各个加工小组的调度信息，我们将每个加工小组对应的调度称为子调度。本文采用子调度维持交叉算子，即在两个父代染色体作交叉运算时，在两个父代染色体中的各取一个子调度复制到后代中，然后用另一个父代染色体剩余的编码按顺序来完成该后代的构造。交叉过程具体描述如下：

1）从一个父代染色体中找到字符“0”所在的位置，建立一个空白后代染色体，并将父代染色体中的字符“0”复制到后代染色体相应的位置；

2）从该父代染色体中随机取出一个子调度，并将其填入所建后代染色体中的相应位置；

3）在另一个父代染色体中，将与步骤2)所取出的子调度相同的基因标记为“-1”；

4）从左到右扫描另一个父代染色体不为“0”和“-1”的基因，依次将其填入到后代染色体的其余位置。

例子：假设有2个父代Pl和P2，随机选择Pl和P2最右边的子调度作为维持的子调度，交叉运算执行过程如下所示：

父代Pl：1 2 3 0 4 5 6 0 7 8 9

父代P2：2 5 8 1 0 3 4 0 6 7 9

中间执行过程：

父代Pl：1 2 3 0 4 5 -1 0 -1 8 -1

父代P2：2 5 -1 1 0 3 4 0 6 -1 -1

后代Cl：××× 0××× 0 7 8 9

后代C2：××××0×× 0 6 7 9

结果：

后代C1： 2 5 1 0 3 4 6 0 7 8 9

后代C2： 1 2 3 4 0 5 8 0 6 7 9

从上例可以看出，染色体的某一基因片段保持不变，其余基因顺序将被调整，部件在前工序的加工小组分配和加工顺序也将被调整。

2.7 变异算子

根据染色体编码的特点，本文采用随机互换两个基因位置的变异方式，随机交换的基因可以是工件号和工件号，也可以是工件号和“0”的不同组合，所以存在下面4种变异形式：

1）如果两个基因都是工件，可能出现两种情况。一种情况是两个工件在同一加工小组上加工，这时实质是改变工件的加工顺序，如下所示：

变异前：1 3 4 0 5 6 0 7 8 9

变异后：1 4 3 0 5 6 0 7 8 9

2）另一种情况是两个工件在不同的加工小组上加工。这时变异改变染色体的工件顺序和工件对加工小组的分配，如下所示：

变异前：1 2 3 4 0 5 6 0 7 8 9

变异后：1 2 7 4 0 5 6 0 3 8 9

3）如果两个基因都是“0”，则把两个加工小组上的加工任务对调，工件的加工顺序不变，如下所示：

变异前：1 2 3 4 0 5 6 0 7 8 9

变异后：5 6 0 1 2 3 4 0 7 8 9

4）如果一个基因是“0”，另一个基因是工件，则工件的加工顺序和工件对加工小组的分配都发生改变，如下所示：

变异前：1 2 3 4 0 5 6 0 7 8 9

变异后：1 2 3 4 0 5 6 7 0 8 9

3 应用实例

在某模具企业运用本文所提的方法，对14个不同时到达车间的部件进行排序，各部件包括的工件数量见表1。将各件的到达时间用三角模糊数表示，见表2。将各工件在设备上的加工时间用梯形模糊数表示，在前工序车间有大宇和威力两个型号的数控机床，见表3和表4。

表1 各部件包括的工件数量（单位：个）

表2 各部件的到达时间（单位：小时）

表3 各部件Ji对应的工件在前工序各设备的加工工时（单位：h）

表4 各部件Ji对应的工件在后工序各设备的加工工时（单位：h）

在上述给定条件下，应用本文的遗传算法求解，设置运行环境为初始种群染色体数为20个，交叉率为0.5，变异率为0.03，遗传代数为12。通过eM-Plant仿真,发现最好的染色体出现在第9代，第10代，第11代，第12代。均为：[1 3 6 10 14 7 11 0 2 4 8 9 12 13 5]，各机床的计划负荷甘特图如下图2所示。

图2 前工序各机床的甘特图

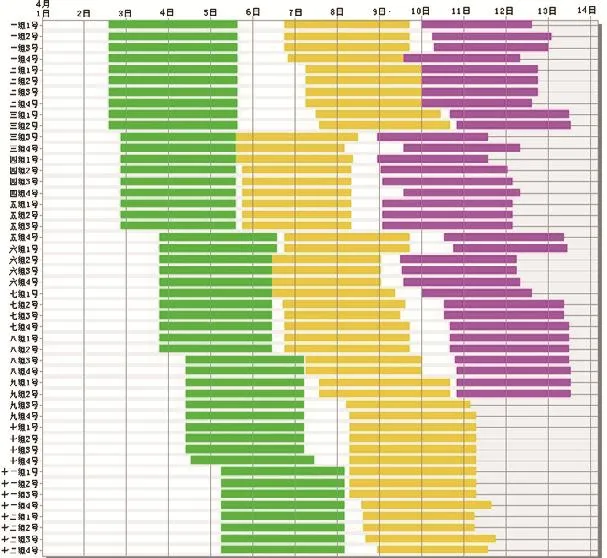
图3 后各机床的甘特图

运用本文提出的遗传算法所有工件通过两道工序的时间是325小时。如果按先到达先加工的原则确定工件的加工顺序，通过两道工序的最大完成时间是369小时，单纯按照Johnson法则确定工件的加工顺序，最大完成时间将是415小时。从这些运行结果对比可以看出，该遗传算法的排序结果优于其它算法，而且计算时间为半秒，适合应用于车间现场。

4 结束语

本文研究了前阶段带有成组约束的两阶段柔性同序加工车间的排序问题，考虑了具有模糊加工时间和模糊到达时间的情况，分别用梯形模糊数和三角模糊数来表示加工时间和到达时间，采用均匀分布的Lee-Li法将模糊数转化为精确值，通过遗传算法优化排序，应用企业的实际算例仿真说明该算法的有效性和可行性。

[1] 孙吴胜.考虑后工序带有成组特征的模具电极调度策略的研究[D].广州:广东工业大学.2007.

[2] 黄锦钿,陈庆新,毛宁.具有成组约束的柔性同序加工车间的排序算法[J].工业工程,2011,V14(2):112-117.

[3] Slowinski R,Hapke M.Scheduling under fuzziness[M].New York:Physica-Verlag.2000.

[4] J.Peng,B.Liu,Parallel machine scheduling models with fuzzy processing times[J],Information Sciences,166,49-66,2004.

[5] 卢永超,陈庆新,毛宁.基于遗传禁忌搜索算法的模具电火花车间调度[J].工业工程,2008,11(5):80-85.

[6] 卢永超,陈庆新,毛宁.模具电火花加工车间的非同等并联机混合遗传算法[J].计算机集成制造系统,2009,15(3):587-543.