波动量法中临界电流数据筛选策略的可行性研究

李 洋，刘自发，王诗超

(1.华北电力大学 电气与电子工程学院，北京 102206;2.广东省电力设计研究院系统规划部，广东 广州 510010)

0 引言

随着电力市场的快速发展，供电公司必须保证供电的可靠性、供电质量和服务水平。然而，由于电力电子技术的迅猛发展，公用电网的谐波问题日益严重。因此，相关部门必须采取有效治理谐波的措施来保证高质量的电能。为合理规范负荷侧对电网的谐波污染，合理地衡量谐波的危害程度成为当务之急[1]。谐波发射水平是衡量谐波危害程度的重要指标。所以，深入研究谐波发射水平显得尤为重要[2～4]。谐波电压发射水平的估计方法主要围绕系统侧等值谐波阻抗的估计来展开，因此谐波发射水平问题的关键在于系统谐波阻抗的估计方法。

文献[5～9]提出了基于干预式法的系统谐波阻抗估计方法，通过改变系统的运行状态产生特定的谐波电流，利用该谐波电流估计系统谐波阻抗;文献[10]阐述了通过双线性回归法估计系统谐波阻抗的方法，该算法可以同时估计出系统侧和用户侧的谐波阻抗;文献[11]描述了采用波动量法估计系统谐波阻抗的方法，通过量测PCC处谐波电压和谐波电流波动来估计系统谐波阻抗(或负荷谐波阻抗)。干预式方法会对电力系统的正常运行产生不利影响，且当PCC处的背景谐波与注入电流频次相同时，将有较大的估计误差;双线性回归法的回归方程缺乏稳定性，误差大，估计精度不高。这几种方法均不宜在工程中使用。波动量法由于估计方法简单、估计准确度高，在提高设备测量精度的前提下，具有很强的工程应用前景。

由于波动量法需要对数据进行大量的采集，通过等间隔求差值的方法获得大量的谐波电压、谐波电流波动量。这些波动量大部分能准确地反映谐波电压和谐波电流的波动程度，从而能得出可靠的谐波阻抗估计值。但依然存在部分波动量值并不能用于谐波阻抗估计，对于此类波动量，我们应当筛除，从而提高利用波动量法进行谐波阻抗估计的精度。目前，波动量法的筛选策略多采用数理统计学方法对谐波电压、谐波电流的波动量数据进行筛选。文献[13]描述了临界电流筛选策略，以临界电流为标准，依据可描绘出电压、电流波动量的幅值关系的曲线来进行波动量筛选。

本文通过PSCAD仿真软件，构造了仿真模型，进行蒙特卡罗仿真，再利用MATLAB软件进行曲线拟合，研究临界电流数据筛选策略是否可以有效地提高谐波阻抗估计值的精度，从而准确地估计出用户侧谐波发射水平。

1 波动量法的基本原理

一般来说，系统谐波阻抗受系统短路阻抗影响较大，当运行方式固定时，短时间内系统谐波阻抗较为稳定，不会有大的波动，相对来说，用户侧的谐波源波动较大，利用被测电压波动量对电流波动量比值的符号特征来估计谐波阻抗和谐波发射水平。

由系统的诺顿等值电路有:

图1 系统的诺顿等效电路Fig．1 Norton equivalent circuit of the system

则有:

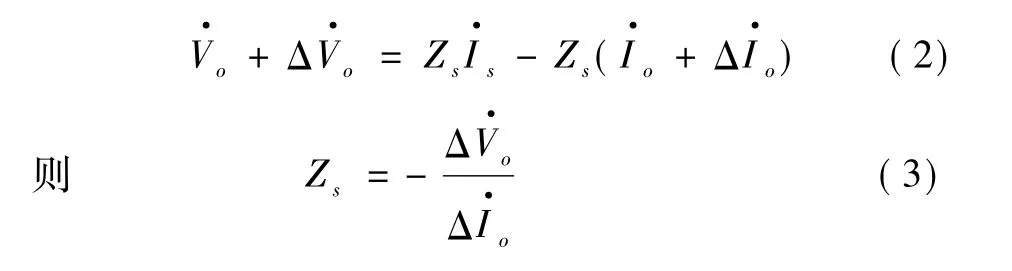
从上述可知，我们测得了公共电气耦合点的谐波电压和电流，再使用这些数据计算出值，由于在实际系统中，阻抗的电阻部分都为正，即 Re[Zs]≥0 并且 Re[Zc]≥0，则定义就有:

当Re[Zk]≥0时，用户侧的谐波电流明显发生改变，则Zk是相应的Zc的估计值;

当Re[Zk]≤0时，系统侧的谐波电流明显发生改变，则 －Zk是相应的Zs的估计值。

通过一系列的测量，建立在大量的数据分析的基础上，可以得到用户侧和系统侧的谐波阻抗并可以减少误差，但是，如果谐波电压和谐波电流的变化太小，波动值和噪声可能是同一水平，估计值就不再有意义了。

得到了谐波阻抗，就可以计算出谐波发射水平为

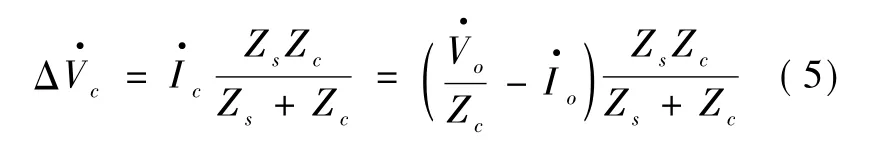
由于Zs表示的系统的短路阻抗，因此，Zs符号Zc，所以就有:

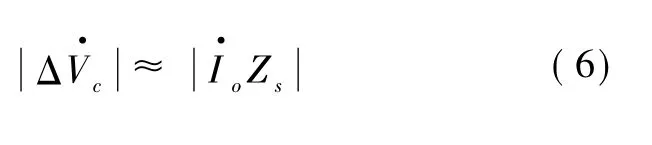
在估计出系统侧的谐波阻抗Zs后，也可根据测量得到的PCC点的谐波电压和谐波电流，从而得出系统侧的谐波电压再根据就可以算出用户侧的谐波发射水平。

2 临界电流筛选策略的基本原理

文献[13]描述了一种筛除不良电压、电流波动量的方法，依据可描绘出电压、电流波动量的幅值关系的曲线来进行波动量筛选。一般来说，系统谐波阻抗受系统短路阻抗影响较大，当运行方式固定时，短时间内系统谐波阻抗较为稳定，不会有大的波动，相对来说，用户侧的谐波源波动较大，以此原理来估算Zs，Zc值。依据采样点计算出 ΔVok，ΔIok(k=1，2，3…．n，其中 n 为采样点数)，再以谐波电流波动差值和作为横轴，谐波电压差值和作为纵轴，绘出两者关系曲线，如图2所示。

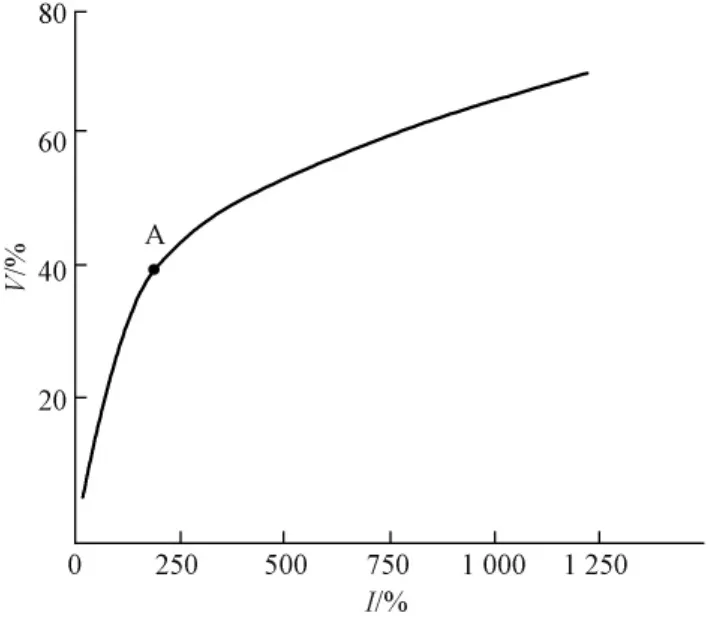
图2 和的关系图Fig．2 the relation betweenand

不难看出A点为转折点，其左边曲线的斜率与负荷谐波阻抗大小有关，右边曲线的斜率反映系统谐波阻抗大小。A点处的电流为临界电流值Icv。只要 ΔIok＞ Icv，即可用于估计系统谐波阻抗值。

3 可行性研究分析

本文为验证该方法的有效性和可行性，通过PSCAD仿真软件，构造了仿真模型，再利用MATLAB软件进行曲线拟合，评估临界电流数据筛选策略在波动量法中的作用。

我们采用PSCAD仿真软件建立双谐波源模型，见图3。其中，系统侧基波阻抗为20+20j(Ω)，负荷侧基波阻抗为20+200j(Ω)。设定系统侧Is1幅值为500 A、相角为0°，负荷侧 Ic5幅值为20 A、相角为0°，负荷侧Ic7幅值为5 A、相角为30°。系统侧、负荷侧二次谐波电流源Is2和 Ic2的幅值在[0，100]A内波动，Is2和Ic2的相角在[0°，180°]内波动。波动频率为10 Hz。

图3 仿真电路图Fig．3 Circuit simulation

进行4次仿真，获得4组仿真算例。每次仿真需量测10 000组PCC处的二次谐波电压、二次谐波电流数据。通过MATLAB软件对每次仿真量测的电压、电流数据分别进行处理。每组算例的计算结果均包含以下几部分:系统侧二次谐波阻抗幅值估计值、幅值误差值σ和二次谐波电压、谐波电流波动量幅值的关系曲线。其中，σ 为与真实值之间的相对偏差，表达式为

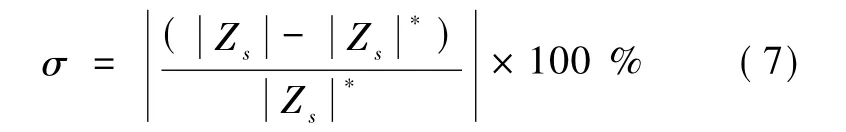
对4幅图进行筛选，得到一些算例的关系曲线有明显的拐点，如图4所示。

列举出几个典型估计结果如表1所示。其中，系统侧二次谐波阻抗幅值的真实值为44.721 36，Ω。

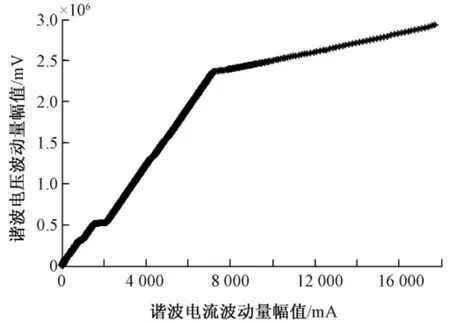
图4 二次谐波电压波动量幅值和电流波动量幅值的关系Fig．4 The relationship between the amount of currentfluctuation and 2 harmonics voltage fluctuation amplitude

表1 二次谐波的典型数据Tab．1 Typical date of the 2 harmunics

图4是算例3的曲线图，由图4和表1知，没有经过临界电流筛的点，获得的系统侧谐波阻抗估计值与真实值相差甚远，估计值幅值误差也非常大。而利用临界电流进行坏点筛除，仅保留大于临界电流值的谐波电流波动量以及相对应的谐波电压波动量，通过这些值进行系统侧谐波阻抗估计，则可获得幅值误差较小的估计值。

为进一步验证该方法的可行性，对仿真模型进行修改并进行蒙特卡罗仿真，利用随机参数设定来实现。将对二次谐波的分析改为对三次谐波的分析，即其中系统侧含Is1和Is3;负荷侧含Ic3，Ic5和Ic7。其他参数设定不变。其中三次系统侧谐波阻抗幅值真实值为63.245 5Ω。进行1 250次蒙特卡罗仿真，每次仿真需改变一次Is3和Ic3的幅值相角的波动范围，幅值波动范围从[0，100]A内随机选取，相角波动范围从[0°，180°]内随机选取，并量测10 000组PCC处的三次谐波电压、三次谐波电流数据。

对1 250组算例的曲线图进行分析，统计得出97组算例的曲线具有明显的转折点。如表2为几个典型估计结果，图5为算例1的关系图形。

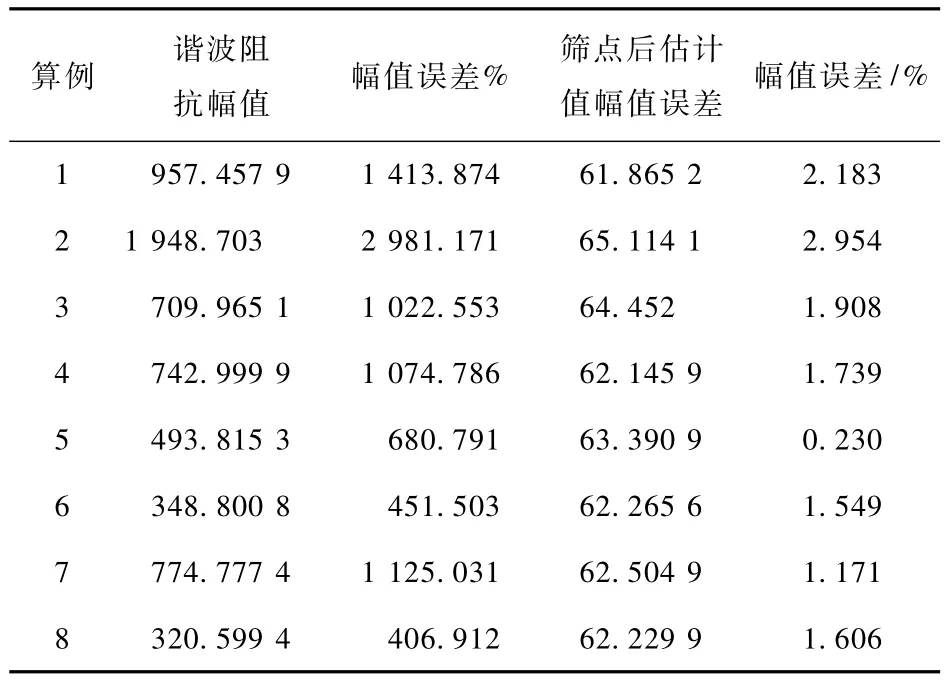
表2 三次谐波的典型数据Tab．2 Typical date of the 3 harmunics

图5 3次谐波电压波动量幅值和电流波动量幅值的关系Fig．5 The relationship between the amount of current fluctuation and 3 harmonics voltage fluctuation amplitude

通过以上大量的仿真数据表明，利用临界电流筛除坏点后，通过保留下的电压、电流波动量进行系统谐波阻抗估计，获得的精度较高。为验证采用临界电流进行坏点筛除的普遍适用性，对出现转折点的97组算例进行分析，对比筛点前后的系统谐波阻抗估计值的分布情况，结果如图6所示。由图6可知，利用临界电流筛除坏点前的谐波阻抗估计值分布规律性较差，变动范围宽且剧烈，并未在某一固定值附近变化。由于系统侧三次谐波阻抗的真实幅值为63.245 59 Ω，图中未筛点前的估计值与真实值相差较大，因此，认为此类估计值不能有效地反映系统谐波阻抗。而观察筛点后的估计值分布图可知，其分布的规律性较强，均围绕在60 Ω左右波动，与真实值较接近，认为此类估计值可较精确地表征系统谐波阻抗值。可见，通过临界电流进行坏点筛除后，系统谐波阻抗的估计值的精度得到了提高。

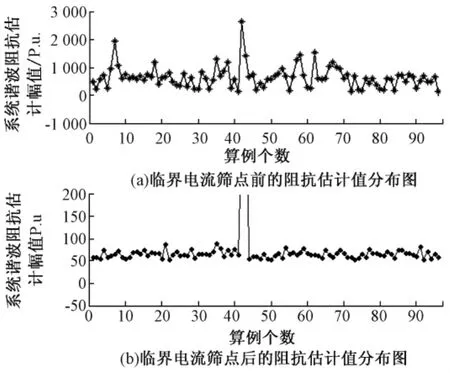
图6 筛点前后估计值分布对比图Fig．6 Estimates of the distribution before and after the screening point comparison

为清晰地量化精度提高的程度，对估计值的幅值误差进行分析，对比筛点前后的估计值的幅值误差的分布情况，结果如图7所示。

图7 筛点前后幅值误差对比图Fig．7 Points before and after the amplitude of the error screen comparison

由图7可知，未利用临界电流进行坏点筛除时，其估计值的幅值误差非常大，经过临界电流处理后，估计误差几乎下降了10倍，误差基本保证在50%以内。说明了临界电流筛选策略的有效性。但我们也发现，该筛选策略能有效地提高估计值的精度，但由于此类估计值的原估计精度极低，因此通过筛选策略处理后获得的估计精度依然不高，估计值的幅值误差依然较大，有近50%的幅值误差值大于10%。所以，临界电流筛选策略能在一定程度上改善估计值精度，但并不能达到最优效果。

前文中提及，存在转折点的曲线被分为两部分，大于转折点的曲线斜率能代表系统侧谐波阻抗，小于转折点的曲线斜率可代表负荷侧谐波阻抗。保留小于临界电流的谐波电流波动量幅值以及相应的谐波电压波动量幅值，依据公式 (4)进行负荷侧谐波阻抗估计，获得97组估计结果，选出几组典型数据如表3所示。仿真模型中的负荷侧三次谐波阻抗的真实幅值为632.455 Ω。

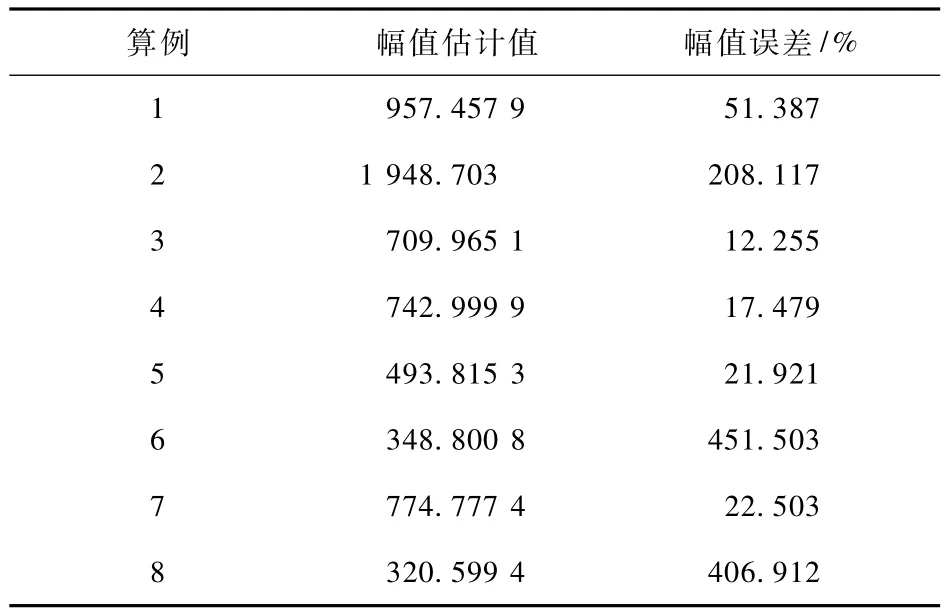
表3 负荷侧三次谐波阻抗幅值估计值Tab．3 The estimate of 3 rd harmonic impedance magnitude at the load side

其中，幅值误差表示负荷侧三次谐波阻抗幅值的估计值与负荷侧三次谐波阻抗的真实幅值之间的差值。97组算例中的谐波阻抗估计值的幅值误差均较大。说明临界电流筛选策略可较准确地筛选出有利于估计系统谐波阻抗的数据，但难以有效地筛选出有利于负荷侧谐波阻抗估计的数据。

通过以上大量的仿真数据表明，利用临界电流筛除坏点后，通过保留下的谐波电压、谐波电流波动量进行系统谐波阻抗估计，可降低估计值的误差，能在一定程度上改善估计值精度，但并不能达到最优效果。

同时值得注意的是，在1 250组算例中仅有97组算例的波动量关系曲线图中存在此类转折点，并且出现转折点的算例的估计值精度都非常低，经过临界电流筛点后的才获得精度相对较高的系统谐波阻抗估计值。未含一个转折点的1 153组算例中，有625组算例的曲线图为一条与直线非常接近的曲线，如图8所示。除此外的算例的曲线图表现得杂乱无章、毫无规律可循，我们可认为是工程条件过于恶劣，导致难以估计除谐波阻抗值。

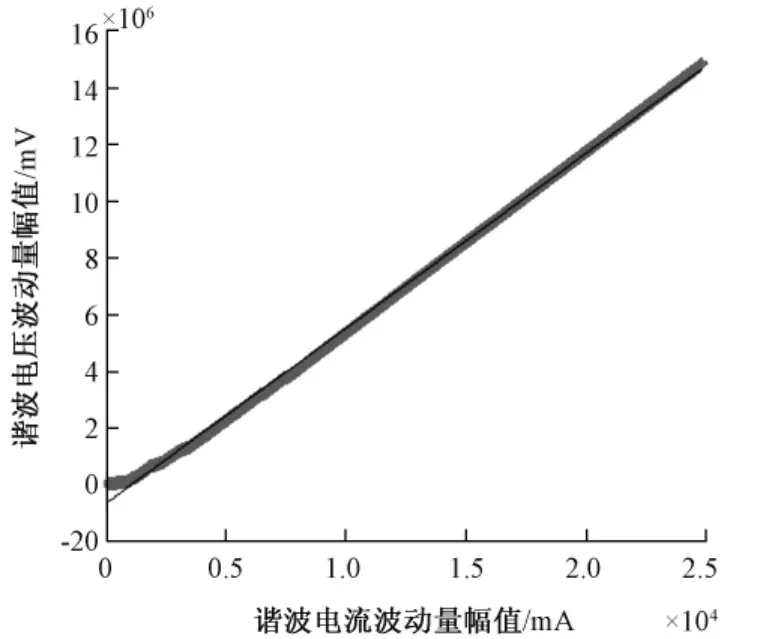
图8 接近直线的电压电流波动量幅值关系曲线Fig．8 The relationship of close to the line voltage and current fluctuations in the amount of amplitude

对这625组算例进行分析，发现这些算例的谐波阻抗估计值一部分在60左右波动，一部分在600左右波动。对所有算例进行分类后绘出其谐波阻抗估计值的分布图，如图9所示。图中的谐波阻抗估计值分为了两部分，我们可认为较小估计值能代表系统谐波阻抗，较大的估计值代表负荷谐波阻抗。说明从此类近似于直线的曲线图中难以区分出估计值究竟是系统侧谐波阻抗估计值还是负荷侧谐波阻抗估计值。

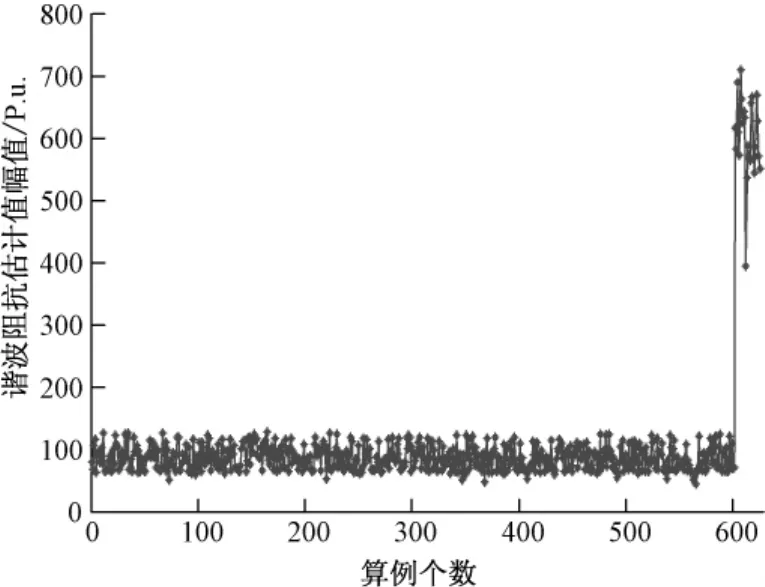
图9 谐波阻抗估计值的分布图Fig．9 The estimate of harmonic impedance

为定量分析此类算例的估计值精度，计算625组算例的幅值误差。对估计值较小的算例而言，其谐波阻抗真实值为系统谐波阻抗值;对估计值较大的算例而言，其谐波阻抗估计值真实值为负荷侧谐波阻抗值。对获得的625组幅值误差进行分析，发现其值均匀分布在0～100%之间。可见，此类算例的谐波阻抗估计值的精度未高于存在转折点的算例的精度，但也远未达到工程精度的要求。则无法通过判定曲线的形状是否为直线，来找寻精度较高的算例，也无法判定获得的估计值的种类。

鉴于上述现象，从物理意义的角度上可理解为，当系统侧波动量远远大于负荷侧波动量时，更接近系统谐波阻抗Zs，因此，电压波动量幅值与电流波动量幅值的关系曲线更接近直线。然而，当不满足该条件时，通过电压波动量和电流波动量的比值获得的系统谐波阻抗估计值的幅值误差较大，公式 (3)不再成立。谐波电压和谐波电流的波动量幅值的关系曲线不再是一条直线的形式，可能会出现转折点，将曲线分为两部分。大于转折点的曲线斜率较接近系统侧谐波阻抗估计值，小于转折点的曲线斜率与负荷侧谐波阻抗相关。

4 结论

(1)临界电流数据筛选策略能有效地提高估计值的精度。未利用临界电流进行坏点筛除时，其估计值的幅值误差非常大，经过临界电流处理后，估计误差几乎下降了10倍，误差基本保证在50%以内。但由于此类估计值的原估计精度极低，因此通过筛选策略处理后获得的估计精度依然不高，估计值的幅值误差依然较大，有近50%的幅值误差值大于10%。所以，临界电流筛选策略能在一定程度上改善估计值精度，但并不能达到最优效果，不能满足较高的工程要求。

(2)临界电流筛选策略可较准确地筛选出有利于估计系统谐波阻抗的数据，但难以有效地筛选出有利于负荷侧谐波阻抗估计的数据。

(3)在实际工程情况中，可能未能绘出存在转折点的关系曲线。如:本文仿真1 250组算例中除97组算例的关系曲线中含有转折点，可利用所述方法进行数据筛选。剩下算例的关系曲线均不含明显的转折点，且这些算例的估计值精度并不都较高，也需要进行劣质数据剔除，则临界电流法不能满足此类数据的筛选要求。可见，该方法在工程上的普遍适用性较差。

[1]Xu W，Lin Y L．A method for determining customer and utility harmonic Contribution at the Point of common coupling．IEEE Transit Power Delivery，VOI.15，No.2，2000．

[2]Srinivasank．On separat ing cu stomer and supply side harmonic contributions．IEEE Trans on Power Delivery，1996，11(2):1003 －1012．

[3]Mou S A，Moussa A M，Blgammal M A．Separation of customer and supply harmonics in electrical power distribution systems．Proceedin-gs of 9th Int ernational Conference on Harmonics and Quality of Power:Vo1 3，October 12，2000，Orlando，FL，USA:1035 －1040．

[4]Xu W，Ahme，Zhang X Q．Measurement of network harmonic impedances:Practical implementation issues and their solutions． IEEE Trans on Power Delivery，2002，17(1):2012－216

[5]YANG H ，Pirottep，Dejaeger E．Harmonic emission levels of industrial loads statistical assessment．CIGRE:Report 362306，August 25，1996，Paris，France:8p．

[6]赵勇，张涛，李建华，等．一种新的谐波源简化模型．中国电机工程学报，2002，22(4):46－51．

[7]赵勇，沈红，李建华，等．谐波源的识别及其与非谐波源的分离方法．中国电机工程学报，2002，22(5):84－87．

[8]刘秀玲，王洪瑞．电网谐波阻抗的测量及其修正．电力系统及其自动化学报，2007，19(2):55－58．

[9]张巍，杨洪耕．基于二元线性回归的谐波发射水平估计方法．中国电机工程学报，2004，24(6):50－54．

[10]Yang H，porotte R，Robert A．Assessing the harmonic emission level from one Particular Customer．Proceedings of PQA，94．

[11]Chazottes，Deflandre B，Gorgette F T，Martinon，Chataigner J，J C．Estimating the true Customer's contribution to the Powersystem harmonic disturbances．EDF＆CNAM，1997．

[12]龚华麟，肖先勇，刘亚梅，等．基于主导波动量筛选原理的用户谐波发射水平评估方法[J]．中国电机工程学报，2010，30(4):22－27.

[13]CIGRE 36.05/CIRED 2 Joint WG CC02(Voltage Quality)Report．Review of methods for measurement and evaluation of the harmonic emission level from an individual distorting load．January 1999

[14]蒋麦占．谐波电流与谐波阻抗的估算——工业与建筑电气系统谐波问题之二[J]．变频器世界，2006，(01)．

[15]余欣梅．考虑谐波影响的配电网电容器优化模型及相关算法研究[D]．武汉:华中科技大学，2004．