基于负荷分解的短期负荷预测传递函数模型

刘 敏，万志宏，文福拴

(1.广州供电局，广东 广州 510620;2.华南理工大学 电力学院，广东 广州 510640;3.浙江大学 电气工程学院，浙江 杭州 310027)

0 引言

短期负荷预测是电力系统规划和运行的基础，关系到整个电力系统运行的安全性和经济性[1]。负荷需求受用电结构、气候变化、星期类型、需求侧管理等多方面因素的影响，这使得负荷变化呈现出非平稳的随机过程。因此，要对负荷进行准确预测是相当困难的。到目前为止，已提出来多种负荷预测方法，如时间序列分析法[2～4]、相似日法[5]、人工神经元网络[6～8]和支持向量机[9]等。

在上述方法中，基于时间序列分析的预报模型在很多领域包括电力系统短期负荷预测中得到了比较成功的应用。到目前为止，应用于电力系统短期负荷预测的时间序列模型主要为累积式自回归-滑动平均模型 (Auto-Regressive Integrated Moving Average，ARIMA)。由于 ARIMA模型只涉及负荷一个变量，无法描述各影响因素对负荷变化的影响，因此这种方法的预测准确性仍不如人意。为考虑各种相关因素对负荷变化的影响，文献[10]采用了传递函数模型分别对双休日和工作日的负荷进行建模，预测精度因此有所提高，但这种方法存在进一步改善的空间。

在此背景下，以文献[10]的工作为基础，本文做了进一步的研究，以改善负荷预测的准确性。基本思路是首先把负荷分解为周期分量和非周期分量，然而对这两个分量分别进行预测。具体地讲，首先基于历史负荷数据，采用传统分解法提取出负荷变化的周期分量，并得到剩下的非周期分量。在此基础上，采用逐步回归法首先从影响负荷非周期分量的因素中筛选出主要因素，然后发展了预测非周期分量的传递函数模型。最后，用广东电力系统实际负荷数据说明了所发展的短期负荷预测模型的实际效果。

1 负荷分解模型

电力系统负荷一般呈现出以周、日为周期的变化规律。所以，可以将负荷分解为周期分量和非周期分量，以提高预测精度。考虑到每天同一时刻的负荷是等时间间隔的 (相隔1天)，这样每天同一时刻的负荷就组成了等时间间隔的随机时间序列。因此，可以采用时间序列理论[11]对负荷进行分析。时间序列分析主要包括两种模型:a.乘法模型;b.加法模型。这里采用时间序列分析中的加法模型对负荷数据进行分解。这样，对于1天24 h 96个时段 (每15 min一个时段)就有96个加法模型，模型的具体形式如式(1):

式中:Pk，t，Dk，t，Sk，t和 Ik，t分别为历史样本中第 k 天中的时段t的负荷序列、负荷序列的趋势分量、负荷序列的周期分量和负荷序列的不规则分量;n为历史样本天数。

各分量的分离过程如下。

(1)对于具有明显非线性趋势的原始序列，可以采用指数、对数或者多项式函数去除原始序列中的非线性。负荷的趋势分量主要受经济增长影响，考虑到短期内经济增长速度保持不变，因此这里采用线性回归法确定趋势分量Dk，t。

(2)用原始负荷序列减去步骤 (1)所获得的趋势分量 Dk，t得到序列{Yk，t}，该序列中含有周期分量和不规则分量。可以采用式 (2)获得周期分量:

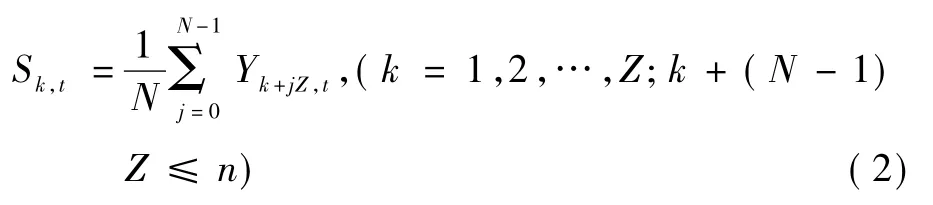
式中:Z为Pk，t周期分量的周期;N为历史数据样本中所包含的周期数。

在提取各分量时，先将负荷数据按照各个时刻分类，形成96个负荷子序列。之后，依次对96个序列提取各分量。这样，序列{Pk，t}是以周为周期的，即Z=7。

(3)用原始负荷序列减去步骤 (1)和 (2)所得的趋势分量 Dk，t和周期分量 Sk，t，求出原始负荷序列的不规则分量 Ik，t。

通过上述步骤可以提取出序列{Pk，t}的周期分量Sk，t，这样就可以预测出待预测日时段 t所对应的周期分量~St。然后，就只需对序列{Pk，t}去除周期分量后得到的序列{Lk，t}建立预测模型，下面将对此展开讨论。

2 数学模型

2.1 变量筛选

由于日最高温度和日最低温度是影响电力负荷的重要因素，而采用前述方法提取出的周期分量Sk，t只与星期类型有关，与日最高气温和日最低气温无关。因此，时刻t的负荷序列{Pk，t}去除周期分量Sk，t后得到的序列{Lk，t}一般会与日最高气温和日最低气温相关。基于这样的考虑，在建立序列{Lk，t}的传递函数模型时，应考虑以日最高气温和日最低气温作为模型的输入量。传递函数模型的输出受到随机事件、日最高气温和日最低气温的共同影响。为简化问题，可以首先对模型的候选输入量进行筛选，剔除相关性较小的输入变量。这里采用逐步回归法[12，13]对输入变量进行筛选。在逐步回归方法中，一般把输入变量称为自变量，把Lk，t称为因变量。逐步回归法每次只引入或剔除一个自变量。一个自变量是否被引入或被剔除则取决于其偏回归平方和的F变量筛选检验结果或校正决定系数的大小。逐步回归法的步骤如下[12，13]:

(1)计算每个自变量与因变量的相关系数r，并根据其绝对值由大到小对自变量排序。选择相关系数绝对值最大的那个自变量进行一元线性回归，并对回归方程进行显著性检验。若回归效果不显著，则说明自变量对因变量的影响不显著。若显著，则进行步骤 (2)。

(2)引入变量。按相关系数绝对值由大到小逐个将自变量引入到回归方程，建立新的回归方程。对引入的变量进行偏回归平方和的F检验。若显著，则引入该变量，否则就不引入。

(3)剔除变量。剔除变量的过程与引入变量的过程相反。

(4)重复步骤 (2)和 (3)，直至自变量筛选结束为止。

2.2 传递函数模型

传递函数模型可以描述自变量与因变量的关系，因此其适于描述Lk，t与日最高气温、日最低气温的关系。为描述方便，给出以下定义:

定义 1 若算子B可以使得:BLk，t= Lk－1，t，BnLk，t=Lk－n，t，则称 B 为延迟算子。

由时间序列理论可知，传递函数模型适用于平稳时间序列。因此，在建立描述Lk，t的传递函数模型前，必须对日最高气温序列{Tk，1}、日最低气温序列{Tk，2} 和序列{Lk，t} 进行平稳化处理。考虑到序列{Lk，t}是负荷序列{Pk，t}去除周期分量得到的，因此可以认为序列{Lk，t}不含有周期趋势。基于上述考虑，为获得平稳时间序列，可以对日最高气温序列{Tk，1}、日最低气温序列{Tk，2} 和序列{Lk，t}分别进行差分运算。若在这三个序列中，存在非平稳序列，则对该序列进行一阶差分运算。若经一阶差分运算后，得到的序列仍为非平稳序列，则对其继续进行一阶差分运算，直至序列平稳为止。

设 {Lk，t} 经过平稳化处理后得到序列{lk，t}，日最高气温序列{Tk，1}和日最低气温序列{Tk，2}经过平稳化处理后分别得到序列{Xk，1} 和{Xk，2}，则Lk，t的传递函数模型可描述如式 (3):

式中:lk，，t为模型的输入时间序列;Xk，i为模型的输出时间序列;Q为经逐步回归筛选后得到的因变量的个数;αk，t为零均值白噪声序列;bi为第i个输入序列的时间延迟;θt(B)=1 － θt，1B － θt，2B2－ … －θt，qBq为q阶滑动平均算子;φt(B) = 1 －φt，1B －φt，2B2－ … － φt，pBp为p阶自回归算子;Ωi(B) =1 － Ωi，1B － Ωi，2B2－ … － Ωi，γBγ为 γ 阶自变量时间序列;Ei(B)=1 － Ei，1B － Ei，2B2－ …－ Ei，μBμ为 μ 阶自变量时间序列。

传递函数模型的建立过程如下[14，15]。

(1)平稳性检验。前已述及，传递函数模型只是对平稳时间序列适用，这样在模型建立之前就必须对输入序列和输出序列进行平稳性检验。这里采用单位根检验法[11]进行平稳性检验，若输入序列和响应序列均为平稳序列，则进行步骤(2)，否则对非平稳序列进行平稳化处理。

(2)预白噪化。对经过适当差分后的输入序列和输出序列利用 Pandit-Wu建模方法[2]建立相应的自回归-滑动平均模型 (Auto-Regressive Moving Average，ARMA)，以产生白噪声序列 {νk，t}和{εk，i}:

式中:Wt(B)=1 － Wt，1B － Wt，2B2－ … － Wt，υBυ为υ 阶自回归算子;Ut(B) =1 － Ut，1B － Ut，2B2－ …－ Ut，ωBω为ω阶滑动平均算子;Γi(B) = 1 －Γi，1B － Γi，2B2－ … － Γi，ρBρ为 ρ阶自回归算子;Hi(B) =1 － Hi，1B － Hi，2B2－ … － Hi，λBλ为 λ 阶滑动平均算子。

(3) 建立预测模型。考察序列 {νk，t}和{εk，i}互相关函数，建立传递函数模型:

式中:{ηk，t}为回归残差序列。

(4)建立残差序列{ηt}的ARMA模型:

3 算例与分析

这里采用广东电力系统2009年5月8日至2009年7月22日的负荷数据以及广东省日最高气温和日最低气温数据作为样本数据，对2009年7月23日的负荷进行预测。短期负荷预测模型建立过程如下。

(1)负荷分解，剔除周期分量。采用第1节介绍的负荷分解模型对各时段负荷组成的序列{Pk，t} 进行分解，剔除周期分量 Sk，t，获得剔除周期分量后的负荷序列{Lk，t}。

(2)采用逐步回归方法筛选出影响 {Lk，t}的主要因素 /变量。以{Lk，t}为指标、日最高气温和日最低气温为候选因素进行逐步回归筛选。现在以2009年5月8日至7月22日0点的、剔除周期分量后的负荷数据{Lk，1}为例来描述筛选过程。计算得知{Lk，1}与日最高气温的相关系数为0.699 9，{Lk，1}与日最低气温的相关系数为0.439 7。这样，在逐步回归中，就先以日最高气温Tk，1为自变量、Lk，1为因变量进行一元线性回归。表1列出了逐步筛选过程中的一些量和相关的检验指标，其中 F1为检验 Tk，1对 Lk，1影响是否显著的统计量，F2为检验 Tk，2对 Lk，1影响是否显著的统计量。

表1 逐步回归Tab.1 The stepwise regression procedure

从表1可以看出，在一元线性回归、引入和剔除过程中，统计量均大于 Fα(这里取 α =0.05)。因此，经过逐步回归后，日最高气温 Tk，1和日最低气温Tk，2均被引入到传递函数模型之中。

(3)建立传递函数模型并进行预测。以步骤(2)筛选出来的主要影响因素/变量作为模型的输入变量，建立 {Lk，t}的传递函数模型，并根据传递函数模型得到待预测日时段t剔除周期分量后的负荷数据的预测值。

(4)待预测日的负荷预测。从负荷周期分量中得到待预测日时段t负荷的周期分量，以及待预测日时段t的负荷预测值。

短期负荷预测流程如图1所示。

图1 短期负荷预测流程Fig.1 The procedure of short-term load forecasting

图2为求得的2009年7月23日的负荷周期分量，图3为该日去除周期分量后的负荷预测值~Lt，图4为该日负荷预测值与实际值。

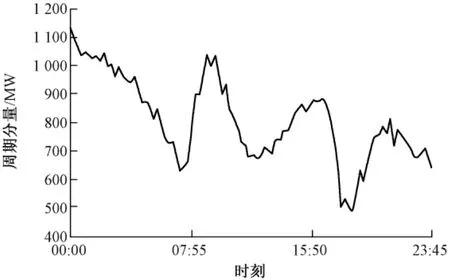
图2 负荷周期分量Fig.2 The periodic component of loads

图3 去除周期分量的负荷预测值Fig.3 The forecasted load with the periodic quantity removed

图4 预测负荷与实际负荷比较Fig.4 Comparisons of forecasted loads and actual loads

为说明本文所发展的预测模型的准确性，这里将本文模型与 ARIMA模型、文献[10]中的模型进行比较。这三种模型在各时段的预测值与负荷实际值见附录A中的表A1。

为了比较这三种模型，这里定义了如下日负荷预测准确率:

式中:Ei为预测日第i个点的相对误差;A为日负荷预测准确率。

从表2可以看出本文模型的日负荷预测准确率高于另外两种模型。

附录A

为更全面地说明所发展的负荷预测模型的准确性，表3列出了三种模型在2009年7月24日至7月30日这一周内的日负荷预测准确率，从中可见本文模型明显优于其它两种模型。

表2 三种模型预测准确率比较Tab.2 Comparisons of load forecasting accuracy indices of three load forecasting models

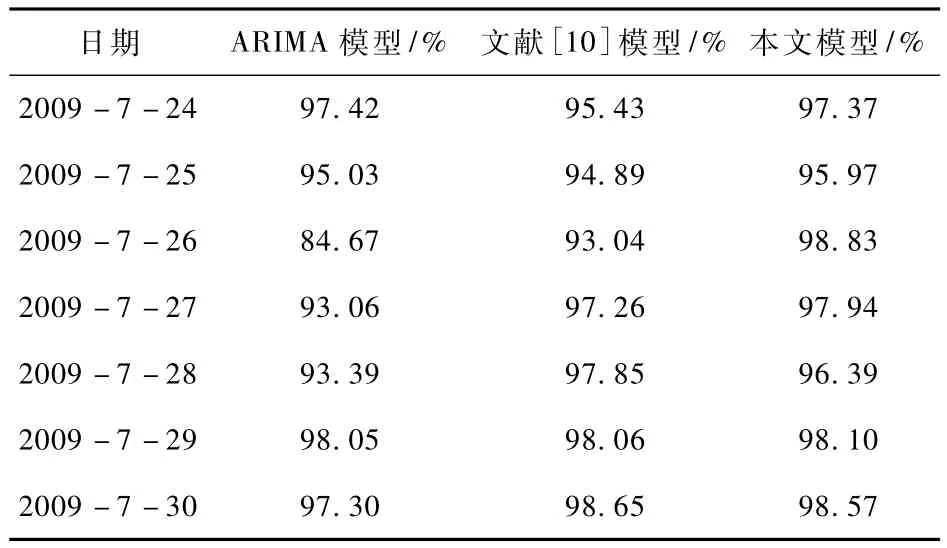
表3 三种预测模型在一周内的预测准确率比较Tab.3 Comparisons of load forecasting accuracy indices of three load forecasting models for one-week period

4 结论

本文发展了一种基于负荷分解的短期负荷预测传递函数模型。采用广东电力系统实际负荷数据所做短期负荷预测结果表明，所发展的方法能够取得较现有的其它两种方法更为准确的负荷预测结果。所发展的负荷预测模型具有下述优点:

(1)该模型能较好反映各种相关因素对负荷变化的影响。

(2)采用负荷分解模型将负荷分解为周期和非周期分量，有效的提高了负荷预测的精度。

(3)采用逐步回归法筛选主要影响因素，也有助于减小负荷预测误差。

表A1 7月23日短期负荷预测结果Tab.A1 Results of load forecasting for July 23

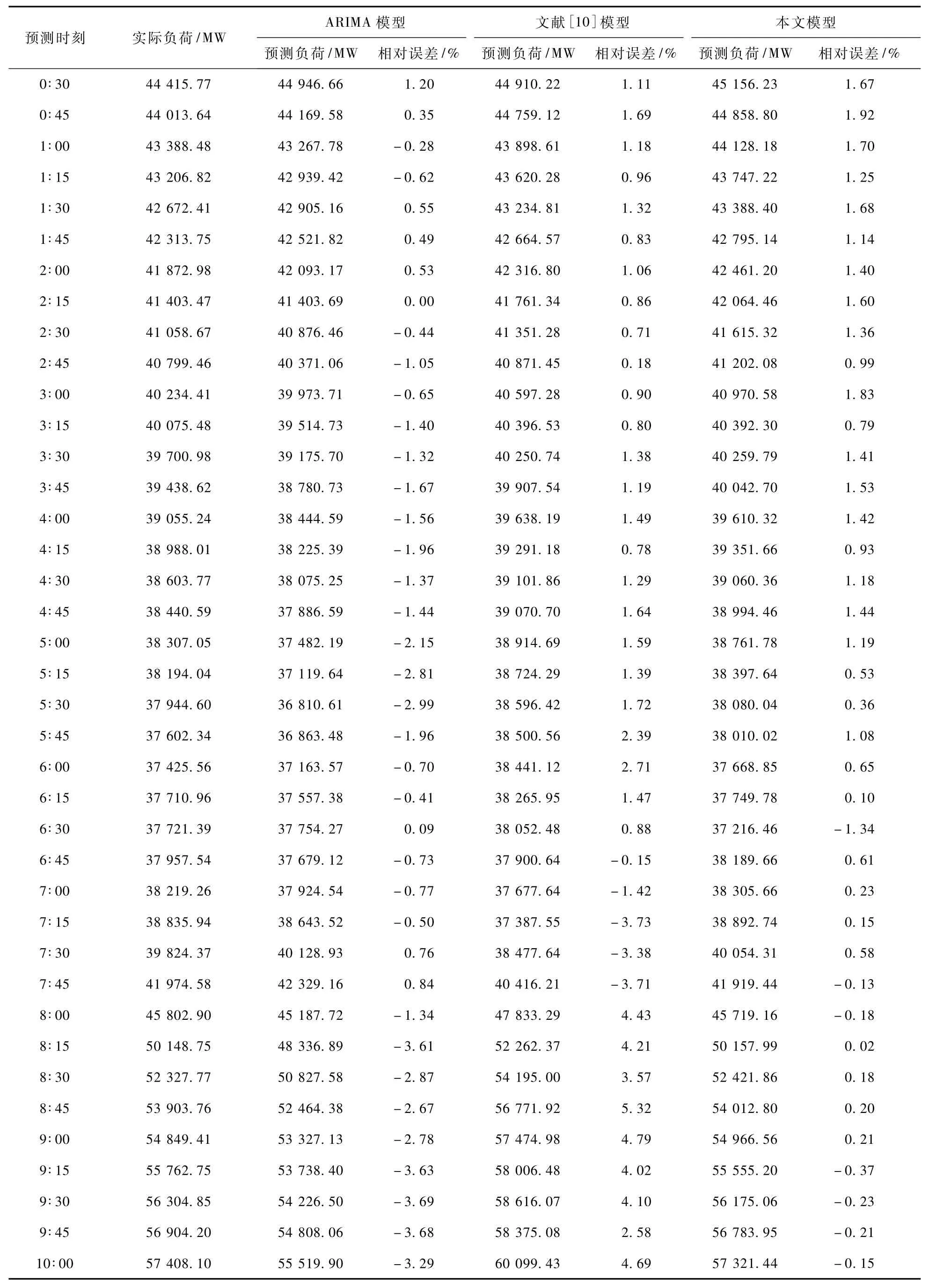
续表

续表

续表

[1]罗滇生，姚建刚，何洪英，等．基于自适应滚动优化的电力负荷多模型组合预测系统的研究与开发[J]．中国电机工程学报，2003，23(5):58－61．

[2]杨叔子，吴雅，轩建平，等．时间序列分析的工程应用[M]．武汉:华中科技大学出版社，2007．

[3]BOX G E P，JENKINS G M．时间序列分析预测与控制[M]．中国统计出版社，1997．

[4]Huang S J，Shih K R．Short-term load forecasting via ARMA modelidentification including non-Gaussian process considerations[J]．IEEE Trans on Power Systems，2003，18(2):673 －679．

[5]莫维仁，张伯明，孙宏斌，等．短期负荷预测中选择相似日的探讨[J]．清华大学学报 (自然科学版)，2004，44(1):106－109．

[6]Hipper H S，Pefreira C E，Souza R C．Neural network for short-term load forecasting:a review and evaluation[J]．IEEE Trans on Power Systems，2001，16(2):44－54．

[7]HiroyukoI M．Deterministic annealing clustering for ANN-termload forecasting．IEEE Trans on Power Systems，2001，16(3):545 －551．

[8]Taylor J W，Roberto B．Neural network load forecasting with weather ensemble predictions[J]．IEEE Trans on Power Systems，2001，17(3):626 －632．

[9]康重庆，夏清，刘梅．电力系统负荷预测[M]．北京:中国电力出版社，2007．

[10]李妮，江岳春，黄珊，等．基于累积式自回归移动平均传递函数模型的短期负荷预测[J]．电网技术，2009，33(8):93－97．

[11]潘红宇．金融时间序列模型[M]．北京:对外经济贸易大学出版社，2008．

[12]何晓群．现代统计分析方法与应用[M]．北京:中国人民大学出版社，1998．

[13]方开泰，金辉，陈庆云．实用回归分析[M]．北京:科学出版社，1988．

[14]SAS/ETS User’s Guide，vision 5 edition[M]．SAS Institute Inc．，Cary，NC，USA，1984．

[15]高惠璇 编译．SAS系统 SAS/ETS软件使用手册[M]．北京:中国统计出版社，1988．