基于多尺度小波分解和时间序列法的风电场风速预测

李东福，董 雷，礼晓飞，廖 毅

(1.华北电力大学 电气与电子工程学院，北京 102206;2.中国南方电网超高压输电公司广州局，广东 广州 510663)

0 引言

由于目前世界能源紧张，电力供需矛盾突出，而常规能源难解燃眉之急，风能作为一种重要的可再生自然能源具有蕴量巨大，可再生性和无污染等优点，所以被公认为是一种理想的可再生能源发电方式。风力发电的输出功率与风电场风速有很大关系，呈现出很强的随机性。对风电场风速进行较为准确的预测，对于电力部门及时调整调度计划，衡量风电场的容量可信度，进而确定合适的风电上网价格，具有重要的现实意义[1～2]。

近年来风电场风速预测的方法较多:神经网络法、时间序列法、卡尔曼滤波法、遗传算法、小波分析[3，4]及其它算法。这些预测方法各有优优势，但也存在一定不足之处，如神经网络法样本训练困难[5，6]，时间序列模型 (ARMA) 的适应性和预测精度问题[7，8]。由于风电场风速序列本身的时序性和自相关性为建模提供了足够的信息，这里的时间序列模型只需要有限的样本序列，就可以建立预测模型，所以得到了广泛的应用，但存在低阶模型预测精度低、高阶模型参数估计难度大的问题[7]，尤其是对于不平稳风序列的预测精度较差;为此本文提出一种基于小波分解和时间序列法的混合建模方式。利用小波分解将各序列分量分别投影到不同尺度上，逐层分解到不同的频率通道上。由于分解后的序列在频率成分上比原始序列单一、平滑，因此分解后序列的平稳性比原始序列好得多。对于非平稳风速时间序列，其小波分解后的重构时间序列就可以考虑用平稳时间序列来处理，对其建立自回归滑动平均模型，很大程度改善了时间序列法对非平稳序列的预测效果。为进一步提高预测精度，模型参数估计和模型定阶过程中分别采用精度较高的最小二乘法与适应性更强的SBC定阶准则[9]。

1 时间序列的小波分解与重构理论

小波分解与重构实质上是通过不同带通滤波器将含有综合信息的一组原始序列分解成多组不同特征的时间序列，一组信号反应原时间序列的内在变化趋势，即逼近信号;其余组的序列反映随机扰动带来的影响，即细节信号[10]。针对不同特征的信号选择不同的参数进行预测。

多尺度小波分解可以通过式 (1)Mallat算法实现。

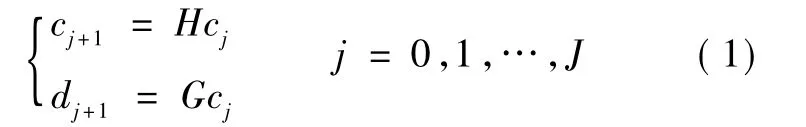
式中:H和G分别为低通滤波器和高通滤波器[8]，小波分解的过程如图1所示。将c0定义为原始序列{V}，于是通过式(1)可以将{V}分解为c1，c2，…，cJ和 d1，d2，…，dJ(J为最大分解层数)，cj和 dj分别称为原始信号在分辨率2－j下的一组逼近信号和多组细节信号。细节信号和逼近信号都是原始序列{V}在相邻的不同频率段上的成分。

经过小波分解后得到的细节序列和逼近序列比分解前的序列点数相应减少，点数的减少会影

图1 小波分解示意图Fig.1 Wavelet decomposition schemes

响最后的预测结果。所以经Mallat算法分解后的各组序列应分别重构回原尺度以增加信号点数，重构算法描述如下:

其中 H*和G*分别是H和G的对偶算子。对c1，c2，…，cJ和 d1，d2，…，dJ分别进行重构，得到 C1，C2，…，CJ和 D1，D2，…，DJ，它们和原始信号 X 的点数一样，并且有:

2 时间序列预测理论

风电场每小时风速数据是随机的动态数据，数据有序性和大小反映了数据内部的相互联系和变化规律，而它们所具有的依存关系或自相关性表征了数据序列发展的延续性，根据时间序列的过去值及当前值来预测未来值[11～13]，可以采用自回归滑动平均模型对平稳风速进行预测。

2.1 自回归滑动平均模型

本文采用ARMA模型对平稳时间序列建模[14～15]，为保证计算精度，减小舍入误差，首先对原始风速序列差分处理消除风速序列的趋势性，同时为适应标准化模型的形式，须对差分后序列 {V(0)t}标准化处理。

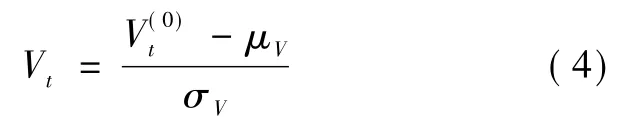
式中:Vt是标准化处理后的新序列{Vt}在t时刻的元素，μV与 σ2V分别为原序列{V(0)t} 的均值与方差的估计值，可由以下两式求得:

根据标准化处理后的风速数据序列 {Vt}，可以建立如下的自回归滑动平均模型 ARMA(n，m):

式中:φi(i=1，2，…，n) 为自回归 (Autoregressive) 参数;θi(j=1，2，…，m)为滑动平均 (Moving Average)参数; {εt}为残差，当模型合适时它是一个均值为零、方差为 σ2α的正态白噪声过程，即 εt∈ N(0，σ2α)。

按式 (7)计算的风速预测序列 {Vt}，还应将其按下式还原成原始预测风速序列{SVt}:

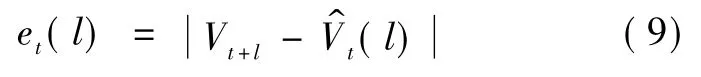
当预测误差的方差值达到指定精度时即认为预测可靠。

2.2 ARMA模型参数估计和适应性检验

模型参数估计和适应性检验是应用时间序列分析法进行建模的关键过程，该过程的适当与否直接影响到模型参数的计算精度和风速预测的好坏。通常模型中的未知参数越多，即自变量越多，模型变化越灵活，模型拟合的准确度就会越高，但未知参数也会增多，未知风险增加，参数估计的难度增大，估计精度反而下降。所以一个好的拟合模型应该是拟合精度和未知参数个数的总和最优配置。

2.2.1 参数估计

模型参数估计的方法很多如:矩估计、最大似然估计、先后估计法等，本文采用最小二乘估计进行参数估计，由于其估计过程充分利用了时间序列观测值的信息，因此估计精度较高。在ARMA(n，m)模型中，即

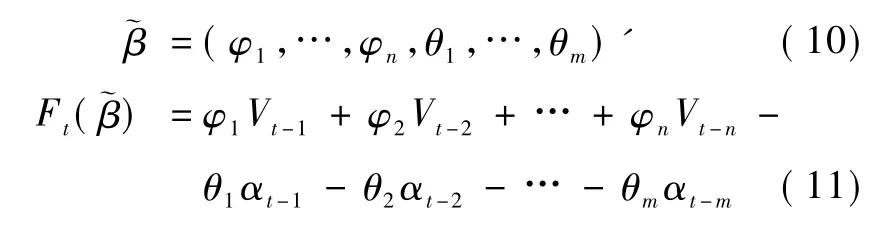
残差项为

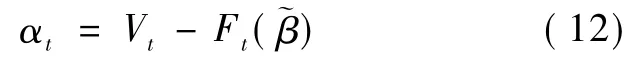
残差平方和为

使残差平方和达到最小的那组参数值即为~β的最小二乘估计值。

2.2.2 模型定阶

常用的建模方法有 Box．Jenkins法、Pandit-WuS．M法以及自回归法等，本文采用 PnaditwuS．M建模方案[9]，即模型定阶时用 ARMA(n，n－1) (n=2，3，4…)，取代 ARMA(n，m)(n=1，2，3…;m=1，2，3…) 模型来进行逐步拟合，缩短建模时间。模型选优过程采用SBC定阶准则，充分考虑到参数个数的惩罚因子和样本容量的关系，避免以往AIC准则在观察值序列越长，相关信息分散时出现的不收敛于真实模型的现象。SBC准则定阶函数[9]定义为

式中:σ2α是残差的方差;p是模型的阶数，对于ARMA(n，m)模型，p=n+m。

其中当公式 (14)函数值SBC(p)达到极小值时所对应的模型阶次p为适用模型阶次。至此，已经确定了时间序列模型的适当阶数与参数，在此基础上就可以对时间序列的未来值进行预测。

3 基于小波分解的ARMA建模

因为风速序列为非平稳时间序列，不利于直接利用ARMA进行建模，所以本文利用小波分析和时间序列法对风速序列进行混合建模，利用小波分解将原始时间序列逐层分解到不同尺度的频率通道上[10，16]，然后分别将其重构回原尺度进行预测，其基本原理如图2所示[14]。

图2 小波分解重构原理图Fig.2 Wavelet decomposition and reconstruction principle diagram

令V:{v1，v2，v3…}是一非平稳时间序列，对其进行小波分解，并且对分解后各层时间序列分别进行重构，可以得到:

式中:VB={vB1，vB2，vB3…} 为逼近信号的重构结果，G1:{g11，g12，g13…}G2:{g21，g22，g23…}…GN:{gN1，gN2，gN3…}分别为第一层至第N层细节信号的重构结果 。因此i时刻的原始风速为

现已知 { ti|i≤M }时刻的值，要预测 tM+l时刻的值，即vM+l由式 (16)得:

vBM+l为 tM+l时刻逼近风速信号的预测值，g1M+l，g2M+l…gNM+l为各层细节信号tM+l时刻的预测值。对上述逼近风速信号和细节风速信号的预测方法与步骤如下:

(1)对Gj(1≤j≤N)和VB建立式 (7)所表示的ARMA模型，并且根据已知的gji(i≤M)和VBi(i≤M)对模型进行参数估计。

(2)对步骤 (1)中建立的ARMA模型应用式 (14)SBC准则进行适用性检验。

(3)根据式 (7)，采用适应性检验后的ARMA模型对逼近信号vBM+l和各层细节信号gjM+l进行预测，得到 vBM+l和 gjM+l的预测值和。

设 vBM+l和 g1M+l，g2M+l…gNM+l预测值为和由式(16)可得原始风速时间序列V的预测值为

预测算法流程如图3所示。

图3 预测算法流程图Fig.3 Prediction algorithm flow chart

4 算例分析

以某实际风电场200组风速数据中前150组作为样本序列 {Vt}建立预测模型，利用该模型预测其后50组风速值。

4.1 基于常规时间序列分析法的预测

首先对原始风速序列进行差分和标准化处理，图4为前150组原始风速序列二阶差分和标准化处理后的结果，该处理一定程度上消除了原始风速的趋势性，有利于提高预测精度。

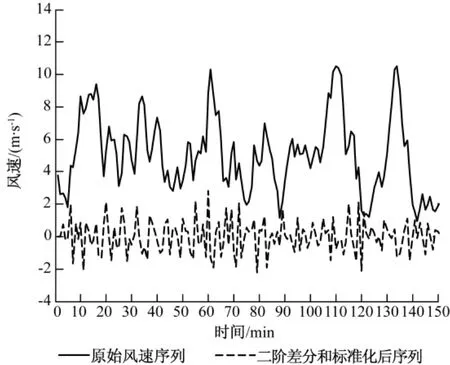
图4 原始风速序列二阶差分和标准化处理结果Fig.4 Second-order difference and standardized treatment results of original wind speed sequence

对标准化处理后的风速序列根据AIC和SBC准则进行模型定阶，由表1可以看出两种计算方式的结果基本一致，ARMA(7，6)模型的AIC值最小，ARMA(6，5)模型的SBC值最小。由于SBC准则相对AIC准则在模型选优过程更具优势，故选用ARMA(6，5)为适用模型。模型定阶后通过式 (10～13)最小二乘法估计ARMA(6，5)的参数，由表2列出。

表1 模型阶数与对应的SBC值与AIC值Tab.1 Model orders and corresponding SBC and AIC value

表2 ARMA(6，5)模型的参数估计值Tab.2 ARMA(6，5)parameters estimation value

为验证拟合模型的准确性，本文根据该预测模型计算后50组的风速值，并与相应的实测风速相比较，结果见图5。

图5 预测风速与实际风速比较结果Fig.5 Forecast wind speed compared with the actual value

由图5可以看出，虽然预测结果一定程度上反映的了风速的变化趋势，但由于差分处理不能很好的消除风速本身的不平稳性，所以预测误差较大，同时预测值也存在不同程度的滞后现象，所以该模型用于不平稳风速分布特性的预测存在一定缺陷。

4.2 多尺度小波分解和时间序列分析的混合预测

首先对原始风速序列进行多尺度小波分解，同时对分解后的逼近信号与细节信号分别重构回原尺度，本文采用Matlab中Biorthogonal小波系的bior3.3小波对风速进行分解重构，分解重构后的风速序列如图6所示:

由图6可以看出多尺度小波分解与重构后的风速序列平稳性与平滑行更好，相似的细节信息更集中，充分体现了风速序列的各尺度详细信息。对分解与重构后的逼近序列与细节序列利用4.1中时间序列分析法进行分层预测，结果如图7所示。

对各层风速序列的预测结果进行叠加合成最后的预测结果，同时将预测结果和原始风速序列进行对比，如图8所示。

图6 原始风速的小波分解与重构图Fig.6 Wavelet decomposition and refactoring of the original speed

图7 各层风速序列的预测结果Fig.7 Forecast result of wavelet decomposition and refactoring series

由图8可以看出，基于小波分解和时间序列法的混合预测法精度更高，预测误差均在5%以内，预测效果较好，证明了模型的有效性。

原始风速小波分解过程中，还存在着分解层数如何确定的问题，小波分解的特性是越往下分解，风速序列划分得越细，逼近信号和细节信号的平滑性和平稳性也越好，但是由于在分解过程中必然会存在计算上的误差，分解层数越多，误差累积的越大，该误差会带到预测的误差中，使预测精度下降。因此选择风速序列分解层数应适宜。表3给出了不同小波分解层数 (2～8)，本文方法的风速预测误差。

图8 混合法预测值与原始风速对比结果Fig.8 The forecast result of hybrid method compared with the actual value

表3 不同分解层数误差比较Tab.3 Error comparison of different decomposition layers

由表3可以看出，当分解层数为4～5时，预测误差基本达到最小，因此在选择分解层数时，如果风速时间序列数据量不是很大，则分解层数一般可以选择4～5层。

5 结论

(1)混合预测方法将不平稳风速序列分解为不同尺度的平稳序列，既弥补了风速不平稳性对预测精度的影响，也充分利用了时间序列分析法对平稳序列的预测优势，一定程度上提高了预测精度。

(2)采用SBC准则的模型定阶方法，考虑了参数个数的惩罚因子和样本容量的关系，避免了观察值序列越长，相关信息分散时出现的不收敛于现象，提高了模型的适应性。

(3)为更好的保证预测准确性，应选择适宜的小波分解层数，同时考虑到在较长时间下时间序列相关性减弱与相关信息分散的特性，预测时间也不宜过长。

(4)本文方法也同样具有风电场风功率预测与分析的应用前景。

[1]张硕，李庚银，周明．含风电场的发输电系统可靠性评估[J]．中国电机工程学报，2010，30(7):8－14．

[2]孙建锋．风电场建模和仿真研究[D]．北京:清华大学，2004．

[3]邰能灵，候志俭，李涛，等．基于小波分析的电力系统短期负荷预测方法[J]．中国电机工程学报，2003，23(1):45－50．

[4]谢宏，陈志业，牛东晓，等．基于小波分解与气象因素影响的电力系统日负荷预测模型研究[J]．中国电机工程学报，2001，21(5):5－10．

[5]韩爽．风电场功率短期预测方法研究[D]．北京:华北电力大学，2008．

[6]杨秀媛，肖洋，陈树勇．风电场风速和发电功率预测研究[J]．中国电机工程学报，2005，25(11):1－5．

[7]潘迪夫，刘辉，李燕飞．基于时间序列分析和卡尔曼滤波算法的风电场风速预测优化模型[J]．电网技术，2008，32(7):82－86．

[8]杨叔子，吴雅．时间序列分析的工程应用[M]．武汉:华中科技大学出版社，1991．

[9]王燕．应用时间序列分析[M]．北京:中国人民大学出版社，2005．

[10]张贤达，保铮．非平稳信号分析与处理[M]．北京:北京国防工业出版社，1998．

[11]Daniel A R ，Chen A A．Stochastic simulation and forecasting of hourly average wind speed sequences in Jamaica[J]．Solar energy，1991，46(1):1－11．

[12]Lalarukh Kamal， Yasmin Zhara Jarfi． Time series models to simulate and forecast hourly averaged wind speed in Quetta[J].Pakistan Solar energy，1997，61(l):23－32．

[13]Billinton R，Chen H，Ghajar R．Time series models of reliability evaluation of Power systems including wind energy[J]．Microelectronics and Reliably，1996，36(9):1253－1261．

[14]吴义纯．含风电场的电力系统可靠性与规划问题的研究[D]．合肥:合肥工业大学，2006．

[15]杨位钦，顾岚．时间序列分析与动态数据建模[M]．北京:北京工业学院出版社，1986．

[16]程正兴．小波分析算法与应用[M]．西安:西安交通大学出版社，1998.

[17]Ingrid Daubechies．Orthonormal bases of compactly supported wavelets[J]．Communication on Pure and Applied Mathematics，1988，41(11):909 －996．

[18]Ashikhmin M．Synthesizing natural textures[J]．2001ACM Symposium on Interactive3D Graphics，2001，(3):217－226．