改进的主成分分析和最近邻的人脸识别方法
刘永生
(杭州电子科技大学计算机学院,浙江杭州310018)
0 引言
人脸识别技术是一个极具现实意义和使用价值的研究领域。目前,主成分分析(Principal Component Analysis,PCA)和独立分量分析是人脸识别问题中的提取阶段采用的两种主要方法。当人脸图像对齐、集合大小已作归一化处理时,基于PCA的识别方法的性能较好[1]。本文提出改进的PCA特征提取方法,采用最邻近分类器来分类识别测试样本,节约了系统内存资源的开销。
1 PCA特征提取的基本思想
1.1 传统的PCA特征提取
设有N个训练样本,每个样本由其象素灰度组成一个向量xi,则样本图像象素数即为向量xi的维数,M为行象素数乘以列象素数,由向量构成的样本集为{x1,x2,…,xn},该样本集的平均向量为:

平均向量又叫平均脸,则每个训练样本与平均脸的偏差为:

则样本集的偏差矩阵为D,D的维数为M×N:

用式3计算样本集的协方差矩阵C,C的维数为M×M:

为了求M×M维矩阵C的特征值和正交归一的特征向量,直接计算是困难的,同时也是非常浪费资源。为此,提出奇异值分解来优化这一问题。
1.2 改进的PCA特征提取
设 A 是一秩为 r的 n ×r维矩阵,则存在两个正交矩阵:U=[u0,u1,…,ur-1]和 V=[v0,v1,…,vr-1],以及对角阵 B=diag[λ0,λ1,…,λr-1],λ0≥λ1≥…≥λr-1,满足 A=UB1/2VT,UTU=I,VTV=I,其中:λi为矩阵AAT和ATA的非零特征值,ui和vi分别为AAT和ATA对应于λi的特征向量。上述分解称为矩阵A的奇异值分解为A的奇异值[2]。构造矩阵:

这样R是N×N维的矩阵,求协方差矩阵Y的特征向量vi和对应的特征值λi。特征脸子空间为:

式中,V=[v1,v2,…,vN],B=diag[λ1,λ2,…,λN],λ1≥λ2≥…≥λN。
ei称为“特征脸”,任何一幅图像都可以表示为这组“特征脸”的线性组合,用他们的线性组合可以重构得到样本中任意的人脸图像,且图像的信息集中于特征值大的特征向量中,即使丢失特征值小的向量也不会影响图像质量。将特征值按大到小的顺序排序:λ1≥λ2≥…≥λm≥…≥λN,对于某一λm,小于λm的λi数值较小,可以忽略。
一幅人脸图像都可以投影到由[e1,e2,…,em]构成的特征脸子空间中,W的维数为N×m。有了这样一个降维的子空间,任何一幅人脸图像都可以向其作投影,并得到一组坐标系数,称为KL分解系数。每幅图像的特征向量可为:

对于任一待识别样本f,可通过向特征脸子空间投影求出其系数向量z:

z就是KL变换的展开系数向量,为m×1维。将向量z作为表示脸部的特征,把其输入到分类器中进行学习和分类,比直接输入图像灰度值的信息要小的多,同时又很少损失原始图像的信息。实际上,根据应用的要求,并非所有的ei都有很大的保留意义。可以选取对应特征值最大的前m个特征向量,使得:

2 最邻近人脸识别方法
本文采用最近领域[3-5]方法作为人脸识别的分类策略来讲述人脸识别过程,依据最短欧几里得距离作为判定准则,在搜索空间中寻找与测试样本距离最近的训练样本,该训练样本所对应的类别,即是测试样本所属的类别。
设具备访问权限的人数为N,每个人有M张照片,就有M×N个训练样本。每一个人作为一个子类w1,w2,…,wN,每个子类有M 个样本(i表示 wi类中的第k 个样本,k=1,2,…,M)计算待识别图像x与全部训练样本之间的欧几里得距离,并选取其中最短的:

可以认为待识别图像与具有最短距离的样本最可能同属于一个子类wj,即x∈wj。
3 实验结果与分析
该实验在Matlab7.1版本上进行仿真,数据库用的是ORL数据库。该数据库一共有400张照片,40人,每人10张,每张照片是112×92=10 304象素的灰度图。考虑到每个人的10张照片的表情变化和遮挡情况,本文选取十折交叉验证的方法进行验证。
在本实验中,用十折交叉验证测试算法准确性。选取每个个体其中的1张照片作为测试样本,剩余的9张作为训练样本,该库中有40个个体,这样测试样本有40张照片,训练样本有360张照片。对测试样本的40张照片分别进行识别,统计正确识别的照片数,计算识别的正确率。重复做该实验10次,在选取测试样本时,轮流选取,计算每次识别的正确率。这样400张照片都进行了识别,最后计算平均识别率。
3.1 PCA特征提取实验
在PCA特征提取实验中,本文计算出了ORL人脸库中的平均脸和特征脸,从左到右分别是原始图、重构特征脸、带能量值的重构特征脸。如图1所示:
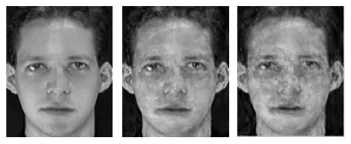
图1 原图和特征脸
3.2 统计分析
选取不同的能量值α,对主分量数和带能量值α的识别率的平均值进行了统计,对每一个能量值α,都要做统计和计算。如表1所示:

表1 不同能量值α的平均识别率
选取不同能量值α,分别计算了不带能量值α的时间和带能量值α时间。如表2所示:

表2 不同能量值α的时间差计算
4 结束语
本文提出了改进的PCA特征提取方法,将传统的PCA方法进行了优化,提高了计算速度和资源利用率。为了提高快速分类识别,本文同时选取了适当主分量数。在分类识别中,采取NNA人脸识别方法,确定待识别图像。通过十折交叉验证方法,验证了改进的PCA和NNA的有效性。该方法获得了较好的识别效果,可供其他科研和工程参考。
[1]Good R P,Kost D,Cherry G A.Introducing a Unified PCA Algorithm for Model Size Reduction[J].Semiconductor Manufacturing,2010 ,23(2):201 -209.
[2]边肇祺,张学工.模式识别[M].北京:清华大学出版社,2000:212-217.
[3]Mohanty P,Sarkar S,Kasturi R.Subspace Approximation of Face Recognition Algorithms:An Empirical Study[J].IEEE Transactions on Information Forensics and Security,2008,3(4):734 -748.
[4]Ni K S,Nguyen T Q.An Adaptable k - Nearest Neighbors Algorithm for MMSE Image Interpolation[J].IEEE Transactions on Image Processing,2009,18(9):1 976 – 1 987.
[5]Mc Names J.A fast nearest- neighbor algorithm based on a principal axis search tree[J].IEEE Transactions on Pattern A-nalysis and Machine Intelligence,2001,23(9):964 -976.

