用SIMULINK的Sigma-Delta调制器行为仿真

何 进，郭裕顺

(杭州电子科技大学电子信息学院，浙江杭州310018)

0 引言

Sigma-Delta是一种得到广泛应用的高精度模数转换器，实际中目前通常由开关电容电路实现［1］。由于这种电路的工作特点，得到一个转换结果需要很多个时钟周期，其分析仿真存在较大困难。通用的电路模拟工具如SPICE虽然可以对这类电路进行仿真，但一次仿真要经历成千上万个时钟周期，需要花费大量的计算时间，因此这样的仿真一般只用于最后的设计验证。设计过程中通常进行的是基于行为模型的行为级仿真方法。按照不同的模型层次，现有的仿真工具可以分成3类:用于概念设计的高层行为仿真、用于设计迭代的中间层等效电路仿真、及主要用于设计验证的底层晶体管级仿真［2］。显然，简单的模型可以得到快速的仿真、复杂的模型能够提供较精确的结果［3］，但要付出较高的计算代价。采取尽量准确的行为宏模型，以在行为级获得与实际电路尽可能接近的结果因此成为减少设计迭代、提高设计效率的关键，也是近年来Sigma-Delta调制器研究中受到很大关注的一个问题［4－6］。本文介绍了一种在MATLAB/SIMULINK中实现的Sigma-Delta调制器行为仿真方法，行为建模时主要考虑了积分器的非理想因素，包括积分器中运放的有限直流增益、有限带宽、摆率和饱和电压。最后通过实例说明这种方法的效果。

1 Sigma-Delta调制器

Sigma-Delta调制器主要由积分器和量化器组成。一阶的调制器如图1所示。它的基本工作原理是:当积分器的输出是正的时候，量化器的输出为正，反馈一个正的信号和输入信号相减，使得积分器的输出向减小;当积分器的输出是负的时候，量化器的输出也为负，反馈一个负的信号和输入信号相减，使积分器的输出增大。

图1 Sigma-Delta调制器的框架图

当调制器工作稳定后，量化输出与输入之间在平均意义上的误差趋于零:

将量化看作是信号与量化噪声的叠加，则输出在z域中可表示为:

U(z)、Q(z)分别是输入信号和化噪声的z域表达式，STF(z)是信号传递函数，NTF(z)是量化噪声的传递函数。对一阶的Sigma-Delta调制器，假定积分器用一个SC积分器实现，其传递函数是:

则输出可表示为:

假定量化噪声是白噪声，根据上述表达式可计算出调制器的信噪比指标。但对实际的调制器，一方面，量化噪声并不完全符合白噪声模型，另一方面，式3描述的积分器模型是理想的，实际积分器包含诸多非理想因素，因此式1到式4只能反映Sigma-Delta调制器的基本功能特性，电路设计需要考虑各种实际因素，作细致的分析仿真。

2 基于SIMULINK的仿真模型

MATLAB/SIMULINK是功能强大的仿真工具，可用于各种工程系统的仿真。Sigma-delta变换器仿真时主要需考虑含积分器的一些非理想因素。本文考虑的积分器非理想因素包括有限直流增益，有限带宽、摆率和饱和电压［4］。考虑上述非理想因素的Simulink模型如图2所示。

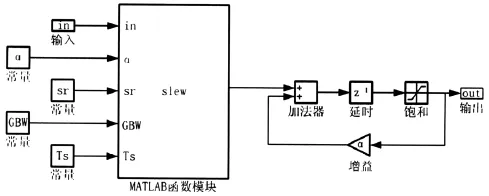
图2 非理想积分器模型

(1)直流增益

实际积分器的直流增益是有限的。有限的直流增益使得输出的反馈只有一部分到达输入端，电荷在开关电容积分器中不能完全被传递。这增加了带内噪声，使开关电容Sigma-Delta调制器的整体性能下降。受此影响，积分器的传输函数变为:

直流增益H0为:

(2)带宽和摆率

有限的单位增益带宽和摆率的影响可以用MATLAB的用户自定义的函数slew表示。图2中在积分器的前端有一个函数模块，从图2中可以看出该模块除了输入信号外，还包括积分器的泄漏α(即alfa)、摆率sr、单位增益带宽GBW和开关时钟周期Ts，由于这些因素，积分器每个时钟周期得到的输出成为［1］:

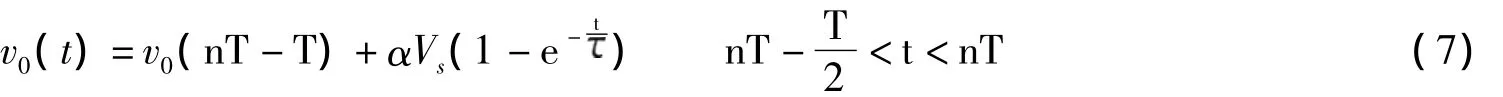
式中，Vs=Vin(nT－T/2)，α代表积分器的泄漏，=1/(2 GBW)，GBW是单位增益带宽。输出电压的斜率最大值位于零时刻，对输出电压求导可得:

当斜率的最大值小于运放的摆率，积分器的输出将不受摆率的限制，可用式7描述输出特性;当斜率的最大值大于运放的摆率，摆率将会限制积分器的输出。输出被分成两个部分，有一个从受摆率限制到不受限制的过程，这个过程可以表示为:

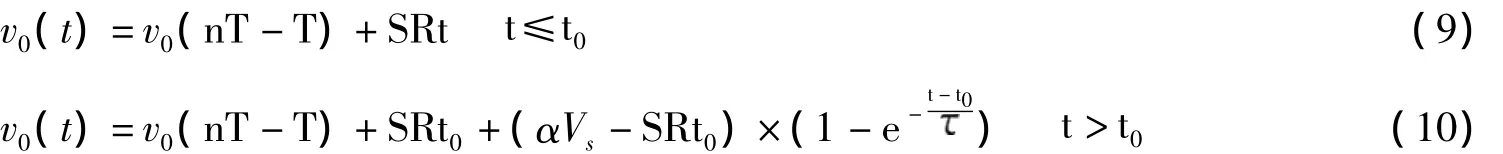
根据函数的连续性可以得到:

(3)输出电压限制

Sigma-Delta调制器的动态范围是设计者主要考虑的因素之一，运算放大器的输出电压的限制将会影响动态范围，所以需要模拟运放输出电压的限制。使用SIMULINK的饱和模块加在积分器的反馈环路中来控制输出。

3 仿真实验结果

为了验证上述非理想积分器的效果，对一个一阶Sigma-Delta调制器分别用SPICE和SIMULINK进行了仿真。选用的调制器如图3所示，开关1和2分别工作在互不交叠的时钟相位，运算放大器的直流增益为80dB，单位增益为5.2MHz，摆率为8V/μs。用SPICE对电路作晶体管级仿真。SIMULINK的仿真模型如图4所示，其中的积分器采用图2的模型。输入信号幅度是0.6V，频率为3 662Hz，采样频率是 4MHz，过采样率为 128，选取采样点数为 16 384，b1=0.5，b2=1。

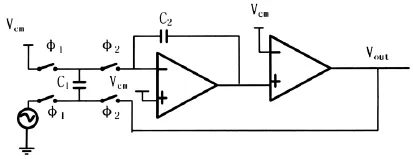
图3 一阶Sigma-Delta调制器

图4 一阶Sigma-Delta调制器的结构

仿真结束后，可得到比较器输出的一个高低电平码流。由于衡量Sigma-Delta调制器的主要性能指标是信噪比和有效位数，因此仿真结束后，还要对数据做快速傅里叶变换得到功率谱，从变换结果中提取信号功率与噪声功率，再按信噪比定义算出SNR。有效位数要先算出信噪失真比SNDR:

再由ENOB=(SNDR－1.76)/6.02得出有效位数。

两种仿真得到的功率谱结果如图5，6所示，可计算出信噪比分别是53.611dB和55.596dB，对应有效位数分别为8.613位和8.943位。对这一调制器，理想情况下的信噪比是62dB，对应有效位数9.97位。可以看出SIMILINK仿真与SPICE晶体管级仿真的结果是较为接近的，但用SPICE的仿真时间为869s，而SIMULINK仅仅需要几秒，大大提高了计算效率。存在的误差说明SIMULINK仿真中尚有未包括的一些实际因素，还需要进一步改进模型。

图5 PSPICE仿真功率谱密度

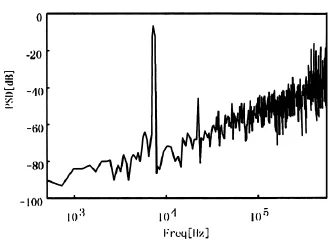
图6 SIMULINK仿真功率谱密度

4 结束语

本文用MATLAB/SIMULINK中实现了Sigma-Delta调制器的行为仿真，仿真时考虑了积分器的一些主要的非理想因素，通过实例验证了这种方法的效果。从仿真结果可以看出，行为级仿真能对调制器性能作较好的预测，同时大大提高了仿真速度，这在设计中是很有意义的。影响Sigma-Delta调制器的非理想因素还包括时钟抖动，开关热噪声等等，同样可以使用SIMULINK对其建模，使这种行为仿真更精确。

［1］Galton I.Delta-sigma Data Conversion in Wireless Transceivers［J］.IEEE Transactions on Microwave Thoery and Techniques，2002，50(1):302 －315.

［2］Dong Y，Opal A.An Overview on Computer-Aided Analysis Techniques for Sigma-Delta Modulators［C］.Canada:IEEE International Symposium on Circuits and Systems，2001:423 －426.

［3］Guo Y，Peng L.Efficient Look-Up-Table-Based Modeling for Robust Design of ADCs［J］.IEEE Transactions on Circuits and Systems，2007，54(7):1 513 －1 528.

［4］Korotkov A S，Telenkov M V.Simulation of Linear and Non-linear Effects in Switched-Capacitor Delta-Sigma Modulators［C］.Proc:IEEE 7th CAS Symposium on Emerging Technologies，2005:58－63

［5］Lei J M，Dai X W，Zou X C.Modeling non-idealities of Sigma Delta ADC in Simulink［C］.China:International Conference on Circuits and Systems，2008:1 040 －1 043.

［6］Malcovati P，Brigati S，Francesconi F.Behavioral modeling of switched-capacitor sigma-delta modulators［J］.IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications，2003，50(3):352 －364.