高精度数控机床主轴伺服控制系统研究

姬清华，连黎明

JI Qing-hua, LIAN Li-ming

（新乡学院，新乡 453000）

0 引言

数控机床主轴驱动系统作为机床的最核心的关键部件之一，其输出性能对数控机床的整体水平是至关重要的。因此就需要开发出技术性能高、价格低廉的交流主轴驱动系统。直接转矩控制技术作为继矢量控制之后发展起来的高性能交流电机控制技术，它直接将磁通和电磁转矩作为控制变量，因此无需进行磁场定向和矢量变换，这种对电磁转矩的直接控制，无疑更为简捷和快速，进一步提高了系统的转矩响应能力，且无超调，系统的动静态品质都很好。[1,2]本文提出了一种基于直接转矩控制的数控机床主轴驱动系统，并将模糊控制与空间矢量调制技术相结合，目的是为了减小转矩和磁链脉动，改善和提高异步电动机直接转矩控制系统控制性能。

1 模糊直接转矩控制系统

在传统直接转矩控制中，一个采样周期中只作用一个电压矢量，该电压矢量根据定子磁链误差和转矩误差从选择表选出，在每个控制周期里，通过合理选择电压矢量，使定子磁链和电磁转矩向各自的给定值变化，从而把转矩和定子磁链误差限制在滞环内，这种控制模式算法简单，转矩响应速度快。但是在数字系统的一个采样周期内，只有有限且不连续的空间电压矢量的选择，并且选择电压矢量时未考虑转速的因素，这样会使转矩急剧地增加或减少，导致转矩的脉动远远超过设定的滞环宽度，使电机产生不希望的噪声和转矩振动。另一方面，逆变器的开关频率是不固定的，滞环比较器的幅值大小影响着开关频率，在数字化的直接转矩控制系统中，由于数字计算的系统滞后、传感器的灵敏度及A/D转换时间等影响，也使在当前采样周期和下一个采样周期之间产生的滞后可能使误差超过滞环宽度，造成磁链和转矩的脉动增大。[3]因此，要实现对直接转矩控制系统的改进，应该以减少转矩脉动和使开关频率固定化为目的。

作为一种智能控制方法，模糊逻辑控制技术为进一步改善直接转矩控制系统的性能提供了有力的支持。将模糊逻辑技术与传统的直接转矩控制相结合，能显著地提高控制系统的动态响应性能，但是在减小转矩脉动方面，提高的幅度不大。主要原因在于可选择的空间电压矢量仍然只有8个，每个采样周期只作用1个电压矢量，开关频率也未提高。[4,5]

因此要显著地减小转矩脉动，改进传统直接转矩控制算法的性能，除了利用模糊逻辑控制技术以外，再结合新的控制策略，就可以进一步提高直接转矩控制系统的性能。空间矢量调制（SVM）技术可以有效地减小转矩脉动，并且在基于SVM 的直接转矩控制中逆变器开关频率恒定，而且在一个采样周期中含有零电压矢量，从而能够有效地抑制转矩、磁链和电流的脉动。

2 模糊SVM直接转矩控制系统

模糊SVM直接转矩控制法将模糊控制技术、空间矢量调制技术与传统的直接转矩控制技术相结合。该算法运用模糊控制器，根据感应电动机定子磁链偏差和转矩偏差以及定子磁链的所在位置，快速、简单和较准确地找到所期望的空间电压矢量us，然后结合SVM技术，用8个基本空间电压矢量来合成，该算法由于采取了SVM技术，因此该算法能保持频率的恒定。控制系统框图如图1所示。

图1 模糊SVM算法的基本框图

2.1 参考电压矢量的获得

能够准确补偿定子磁链误差与转矩误差的电压矢量称为参考电压矢量。定子电压方程为：

式中us为定子电压空间矢量，Rs为定子电阻，is为定子电流空间矢量，s为定子磁链空间矢量。

假设Rsis很小并且可以忽略，则式（1）可以改写为：

当采样时间Δt为恒定值时，定子磁链的变化量几乎与电压空间矢量成正比，并且当有非零电压矢量作用时，定子磁链空间矢量将会迅速变化，其方向与电压空间矢量的作用方向一致，如图2所示。

图2 静止坐标系中的空间电压矢量与定子磁链矢量

从图2可以看出，在静止参考坐标系中，定子磁链的变化Δs可以分解为两个相互垂直的分量Δs和ΔsF，ΔsF影响定子磁链的大小，而Δs影响转矩的大小。期望的空间电压矢量（即参考电压矢量）us*的大小取为一恒定值，而方向为角度*，它由两部分组成，即：

式中， 为偏转角，从图2可知，它由定子磁链偏差Δs和转矩偏差ΔTe得到。当转矩偏差远大于定子磁链偏差时，增大可以快速减小转矩偏差，同理，当定子磁链偏差远大于转矩偏差时， 减小可以快速减小磁链偏差。在启动时，首先要快速建立磁场，此时 可以取得很小。由于 同时影响转矩偏差和定子磁链偏差，而转矩偏差和定子磁链偏差之间的关系不能直接用公式表示，即两者之间不易解耦，所以采取模糊控制的方法来得到偏转角 。

2.2 模糊控制器设计

模糊控制器使用模糊的方法把不同等级的转矩、磁链偏差分成不同的模糊子集，用模糊推理及模糊决策来选择最优电压矢量。

模糊子集为模糊控制器的2个模糊输入变量即转矩偏差ETe和磁链偏差Es的绝对值，和1个输出控制量即期望的参考电压矢量的偏转角 。

转矩偏差ETe是给定转矩Te*（速度PI 调节器输出值）与实际电磁转矩观测值T?之差，其隶属函数如图3所示。磁链偏差Es为定子磁链给定s*与定子磁链实际观测值s之差，其隶属函数如图4所示。磁链偏转角 由定子磁链偏差Δs和转矩偏差ΔTe得到，其隶属度函数为三角形隶属函数，如图5所示。

图3 转矩误差 |ETs| 的隶属函数

模糊控制规则可由|ETe|，|Es|和 来描述，共16 条规则，如图6所示。第i条规则Ri描述如下：

If |ETe| is Aiand |Es| is Bithen is Vi

图4 磁链误差 |Eψs| 的隶属函数

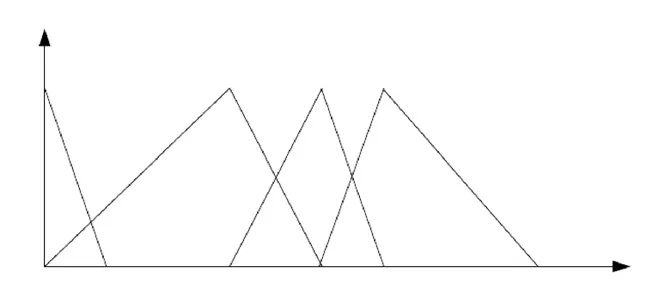
图5 偏转角η的隶属函数

图6 直接转矩模糊控制规则

模糊推理是采用模糊逻辑由给定的输入到输出的映射过程。本文采用Mamdani型模糊推理的max-min合成法，这是一种以模糊关系合成法则为基础的推理方法。

3 基于模糊SVM 控制的直接转矩控制系统的仿真

为了验证所提出的模糊直接转矩控制好方案的有效性和可行性，在Matlab/Simulink 环境下进行了仿真分析。仿真主要参数为：额定电压UN=220V，额定频率fN= 50HZ，额定转速nN= 1440r/min，定子电阻Rs= 0.435Ω，转子电阻Rr=0.816Ω，定子电感Ls= 0.004H，转子自感Lr= 0.002H，互感Lm= 0.124H，极对 p=2，转动惯量 J = 0.089kg ·m2。采样周期50μs，给定参考磁链值为0.9Wb。

为了对比控制效果，先后采用了传统的基于圆形磁链的直接转矩控制方法和改进后的模糊直接转矩控制方法，并给出了不同控制方法时的磁链、轨迹和电流响应曲线，如图7!图9所示。

图7 定子磁链响应曲线

图8 稳态时圆形磁链轨迹

从以上仿真结果可以看出，传统基于圆形磁链的直接转矩控制方法中，磁链、轨迹以及电流的脉动都比较大，而改进后的直接转矩控制中，磁链、轨迹以及电流的脉动都明显减小，而且响应也比传统的要快。说明改进后的直接转矩控制方案能够有效地减小转矩、磁链及电流脉动，并且具有更好的动态响应能力。经过以上对仿真结果的分析，验证了模糊SVM 方法在异步电动机直接转矩控制系统中的可行性。

图9 a相电流曲线

4 结束语

本文研究和分析了一种结合模糊控制技术的电压空间矢量调制（SVM）的直接转矩控制策略，详细分析了其原理与实现，并在MATLAB/SIMULINK环境下进行了仿真分析。仿真结果表明该控制方案既保持了直接转矩控制的快速动态响应特性，又有效减小了转矩与电流的波动。

[1] 张剑, 许镇琳, 潘月斗. 组合机床交流主轴伺服系统全数字检测研究[J].组合机床与自动化加工技术, 2005(2):50-52.

[2] 许海平, 葛琼璇. 数控机床数字交流主轴伺服系统的研制[J]. 新技术新工艺, 2000(8): 6-8 .

[3] D Casadei, G Grandi, G Serra, A Tani .Effects of flux and torque hysteresis band amplitude in direct torque control of induction machines .In 20th International Conference on Industrial Electronics Control and Instrumentation,1994(1): 299-304 .

[4] Bacha F, Dhifaoui R，Buyse H. Real-time implementation of direct torque control of aninduction machine by fuzzy logic controller .Proceedings of the International Conference onElectrical Machines and Systems (ICEMS),2001(2): 1244-1249.

[5] 汤兵勇, 路林吉, 王文杰. 模糊控制理论与应用技术[M].北京: 清华大学出版社, 2002: 1-4.