人机交互领域中Fitts’定律研究

0 引言

人机交互系统的可用性越来越受到研究人员和设计人员的关注，研究方法包括用户测试法、专家评审法和访谈法等，同时提出了多种预测模型，如GOMS模型、击键层次模型和Fitts’定律等。Fitts’定律是其中很重要的一种定量预测模型，在人机交互领域得到了比较广泛的应用，为设计人机交互界面的设计提供了科学依据。

1 Fitts’定律的提出

Fitts’定律是1954年由美国Fitts博士提出的[1]，用于研究指点设备指向目标所需要的时间。该定律指出使用指点设备到达一个目标的时间同以下两个因素有关：

1）设备当前位置和目标位置之间的距离（A）。距离越长，所用时间越长；

2）目标宽度（W）。目标越大，所用时间越短。

该定律可用式（1）表示：

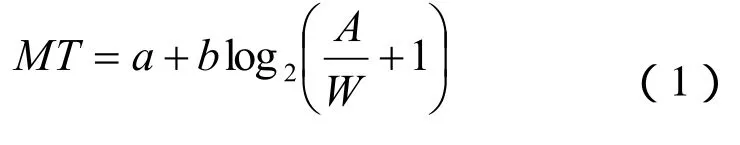
其中MT为执行点击运动所需要的移动时间，a，b是经验系数，其依赖于具体的实验环境。log2(A/W＋1)为任务难度系数（ID，Index of Dif fi culty），表示用户执行任务的难易程度。

2 Fitts’定律在人机交互界面研究中的发展与应用

用Fitts'定律对人机交互界面进行研究时，界面的维度是很重要的一个因素。因此，以界面的维度来划分Fitts'定律在人机交互界面中的应用研究。

2.1 Fitts’定律在一维交互界面中的应用研究

Fitts’定律最初提出来时只适用于一维空间中，即只考虑目标的宽度，假定目标的高度为无限长[2,3]，示意图如图1所示。

图1 Fitts’定律在一维界面中应用示意

2.2 Fitts’定律在二维交互界面中的应用研究

Crossman[4]首次将Fitts’定律引入到二维界面应用中， 提出的观点是“目标的垂直高度对移动时间有显著影响”，并给出了计算公式

式（2）中a，b，c是经验系数，H表示目标的垂直高度。

Hoffmann和Sheikh[5]于1994年进行研究得到的结论为：“目标的宽度和高度是相互影响的”。这一结论与Crossman[4]的研究结论有较大不同。

MacKenzie和 Buxton于 1992年 对 Fitts’定律进行了扩展，提出5个不同的难度系数表达式，分别是：

1）以目标宽度和高度的最小值作为因子，如式（3）：

2）以运动方向上目标“外观宽度”W’作为因子，如式（4）：

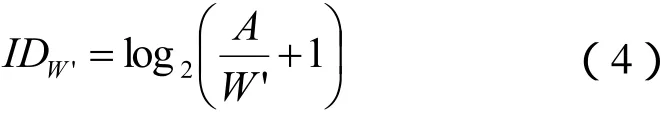
所谓“外观宽度”，如图2所示。

3）以目标宽度和高度的总和作为因子，如式（5）：

图2 目标外观宽度示意图

4）以目标宽度和高度的乘积作为因子，如式(6)：

5）表达式（1）中的难度系数，如式（7）：

结果表明难度系数IDmin(W,H)的计算结果与实验结果最吻合，其次是IDW’。

对于IDW’，从图3（a）可以看出，目标高度对IDW’没有影响；对于IDmin(W,H)，存在的不足主要包括三点，分别如图3（b）、3（c）、3 （d）所示：

1）从图3（b）我们可以看出，如果目标的宽度比高度大的话，那么目标的宽度对IDmin(W,H)没有影响；

2）从图3（c）我们可以看出，移向目标的角度对IDmin(W,H)没有影响；

3）从图3 （d）我们可以看出，变换目标的高度和宽度对IDmin(W,H)没有影响。

为了解决IDmin(W,H)和IDW’两种模型存在的不足， Accot和Zhai[3]于2003年提出了一种带权重的欧几里得模型：

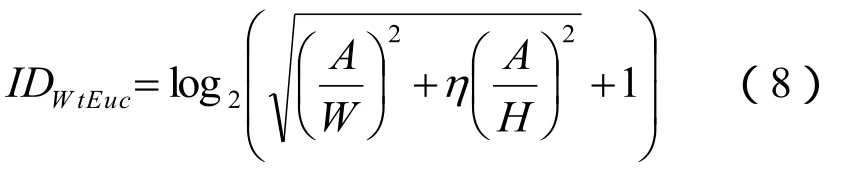
图3 模型缺陷示意图

式（8）中 为经验系数，使得目标的高度和宽度对用户操作的难度系数的影响不同；（A/W, A/H） 为“二维空间中起点到目标的距离”。该模型与IDmin(W,H)和IDW’两种模型相比有了显著的改进，然而，不同的移向目标的角度和目标的不同形状在模型IDWtEuc中还是没有加以考虑。

Fitts’定律应用于儿童产品的设计是目前二维界面中研究的一个热点问题，例如美国的马里兰大学人机交互研究中心Hourcade等进行的一系列研究，以及荷兰的阿姆斯特丹大学人机交互中心的Donker和Reitsma针对儿童使用鼠标的行为进行的一系列研究等。

国内针对Fitts’定律进行的研究主要集中在网站的设计中，如2006年丁宇[6]采用Fitts’定律对电子商务网站的可用性进行研究。

2.3 Fitts’定律在三维交互界面中的应用研究

在三维环境中应用Fitts’定律的研究相对比较少，最早在该方面进行研究的是Ware，他将二维环境下的IDmin(W,H)进行扩展，得到在三维环境下适用的IDmin表达式，如式（9）：

为了改变W, H, D三个因子对IDmin的影响程度， Grossman和Balakrishnan[2]于2004年进行了一项研究，将H, D两个因子前加上了权重因子α和β，得到模型（10）：

2003年Accot和Zhai[3]提出了一个在三维环境下适用的带权重的欧几里得模型，如式（11）：

为了解决二维环境下“没有将移向目标的角度考虑在内”问题， Grossman和Balakrishnan[2]将fW,H,D(θ)影响因子引入到模型（10）中，得到模型（12）：

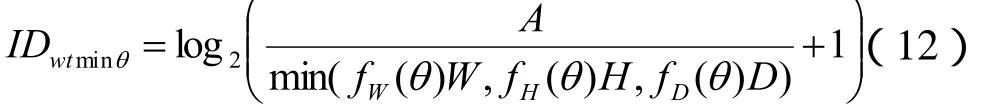
其中 fW(θ), fH(θ), fD(θ)分别表示移向目标的角度θ在不同方向上的影响权重。

将fW,H,D(θ)影响因子引入到模型（11）中，得到模型（13）：

测试用户操作绩效时需要考虑漫游速度，但是上述所有模型中都没有将漫游速度考虑在内，为此，任刚等在2008年进行的一项针对手机三维用户界面ID评估的研究中就将漫游速度引入到模型中，得到模型（14）：

其中v为漫游速度，λ为操作方式的难度系数，f（λ, v）是一个经验公式，表明了在一定的操作方式下速度对操作精度的影响。在三维环境下使用漫游技术进行物体选取所用的时间和距离A、角度θ、漫游速度v以及操作方式的难度系数λ相关，而与三维物体自身的大小和角度无关。

3 结束语

Fitts’定律是人机交互领域重要的预测模型，为人机交互提供了一个度量的法则。

但Fitts’定律在人机交互领域应用时也存在一些局限：Fitts’定律不能描述双手操作时的移动时间；Fitts’定律没有考虑用户执行真实任务时的系统反应时间、用户的思考时间等因素。

Fitts’定律在三维用户界面中的应用研究需要特别加强，需要考虑的因素比二维用户界面多很多，例如如何度量三维界面中目标的宽度，如何设计三维界面中的漫游速度等。

[1] P. M. Fitts. The information capacity of the human motor system in controlling the amplitude of movement [J].Journal of Experimental Psychology, 1954, 47(6): 381-391.

[2] T. Grossman, R. Balakrishnan. Pointing at Trivariate Targets in 3D Environments [C]. Proceedings of the ACM Conference on Human Factors in Computing Systems(CHI), Vienna, Austria, ACM Press, 2004: 447-454.

[3] J. Accot, S. Zhai. Refining Fitts' law models for bivariate po-inting [C]. Proceedings of the ACM Conference on Human Factors in Computing Systems (CHI), Florida,USA, ACM Press, 2003: 193-200.

[4] E. R. F. W. Crossman. The measurement of perceptual load in manual operations [D]. PhD thesis, University of Birmingham, 1956.

[5] E. R. Hoffmann, I. H. Sheikh. Effect of varying target height in a Fitts' movement task [J]. Ergonomics, 1994,37(6): 1071-1088.

[6] 丁宇. 从Fitts定律看电子商务网站的可用性设计[J]. 商场现代化, 2006, 12: 101-102.