干摩擦力学系统的建模及振动响应分析

汪 俊WANG Jun

（广州城市职业学院 信息与汽车工程学院，广州 510405）

0 引言

干摩擦广泛存在于机械系统的摩擦副中，如金属丝减振器，金属橡胶元件，车辆中离合器的主动盘与从动盘的摩擦面中，如图1所示。其减振的频带宽，可有效的降低系统的振幅，是一类行之有效的被动隔振和减振装置，因此得到了工业界的广泛关注。

图1 离合器中的干摩擦交接面

由于干摩擦力学特性的强非线性(如回复力与位移曲线呈迟滞特性)，使得干摩擦元件的设计较为困难，通常依靠经验或大量的试验试制等手段进行设计，成本高，周期长。为此，建立合理的干摩擦力学模型和推导计算量适当的数值方法就显得尤为重要。至上世纪三十年代以来，国内外众多学者对此展开了大量研究。

Den.Hartog在1931年提出了理想的干摩擦模型(coulomb模型)。假设一物体在干摩擦交接面上运动，干摩擦阻力总是阻碍运动，因此，干摩擦力的方向总与运动方向相反，但其大小不变。从时域上看，干摩擦阻力的波形为方波，其变化规律可表示如下：

其中，Ft为干摩擦阻力的大小， 为物体的运动速度。

Den.Hartog的模型表达了理想的干摩擦。然而，大量的实验研究表明，物体与干摩擦表面相接触时，物体速度方向的改变并不是突然发生的，而是存在一个过渡过程。由于接触面本身有一定的弹性，在外力的作用下，造成了接触面有一定的弹性变形。当外力的方向改变时，物体的运动方向并没有立刻改变，当外力的大小增大到一定程度，物体与接触面才产生相对位移。

考虑到接触面的弹性性质，Iwan在1961年提出了著名的双折线迟滞模型，该模型将干摩擦阻力看成一根弹簧和一个标准的coulomb摩擦副串联，且能更好的表达干摩擦阻力的非线性性质。

本文针对一个含有干摩擦元件的单自由度系统，实测了其在谐波激励下出现的粘滑运动，并将计算值与实测值进行了对比。结果表明，文中给出的建模和计算方法是有效的。

1 单自由度干摩擦系统的实验研究

测试对象为一含干摩擦的单自由度系统，图2为测试原理图。由MTS的作动端对物体施加垂直方向的位移激励x (t)＝x0＋xmsin (2π ft)，其中，f为激励频率(Hz)，xm为激励幅值(mm)，x0(mm)为预载。图2中，OA所示的位置是初始位置。在预载x0的作用下，OA由初始位置运动至水平位置OB，然后在水平位置OB附近作往复摆动。

假设在位移激励Δx下，OB运动到了OC。假设OA的长度为l，则的摆角为：

图3为时间-摆角关系的测试结果，可见单自由度系统时间—摆角呈现明显的粘-滑运动。

图2 单自由度运动响应测试原理

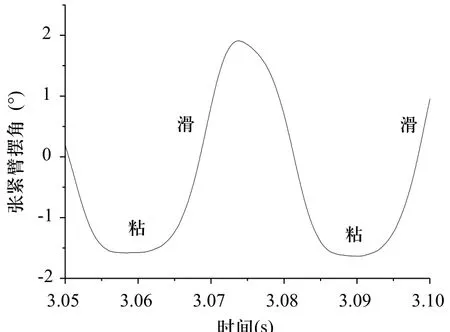
图3 单自由度系统的粘-滑运动

2 单自由度干摩擦系统的力学模型

研究对象为图3所示的振动系统。该系统由两轮、一带和一个集中质量组成。其中，集中质量连接弹簧k (N/m),阻尼c (Ns/m),集中质量受到幅值为P (N)、频率为ω (rad/s)、相位为0度的激励力作用。假设集中质量与带之间的摩擦为干摩擦，则该集中质量的受力情况与图2中的单自由度物体类似。文中只考虑集中质量在力激励作用下的位移的时域响应和频域响应，不计算两轮和带的运动，因此，图1中振动系统可视为单自由度系统。

以地面为参考坐标系，以集中质量的静平衡位置为坐标原点，设集中质量的位移为x (m)且向右为正，带的速度为vb(m/s)，干摩擦为Z (t)，则集中质量的运动微分方程为：

由于干摩擦的作用，使得集中质量的运动出现滑移—粘着—滑移交替出现的情况，因此分别讨论滑移、粘着时的运动方程及相应的解。

其中，Z (t)表示干摩擦的大小为时间的函数，其增量形式的本构关系为：

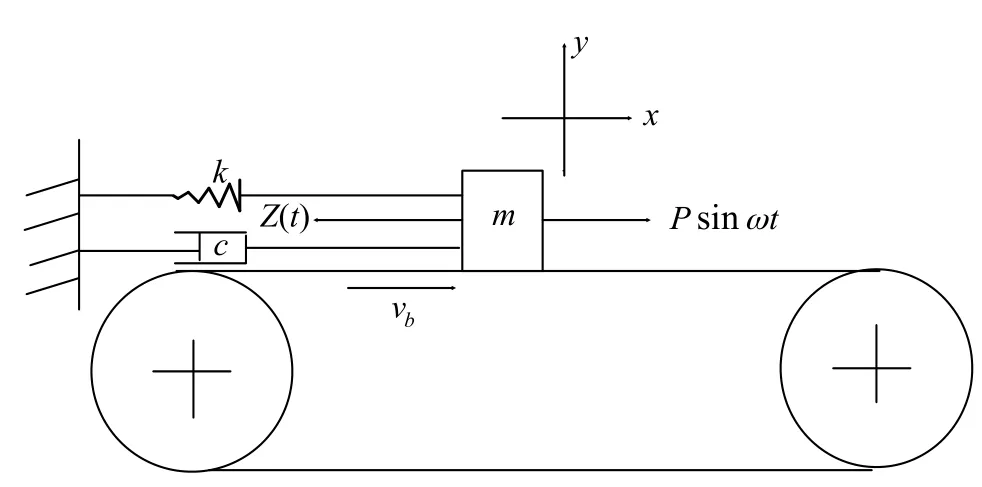
图4 包含双折线模型的单自由度振动系统

3 系统响应的求解方法

由于干摩擦的作用，使得集中质量的运动出现滑移—粘着—滑移交替出现的情况，因此分别讨论滑移、粘着时的运动方程及相应的解。

3.1 集中质量的运动为滑移时的运动方程

当集中质量的运动为滑移时，在用双折线模型描述干摩擦力的情况下，干摩擦相当于刚度为ks的弹簧，因此，式（3）变为：

定义如下的变量：

则（6）变为：

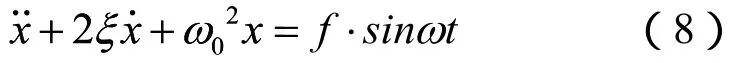
式（8）为二阶常系数非齐次微分方程，其解由对应的齐次微分方程的通解和非齐次微分方程的特解组成。通解只对应于振动响应的过渡阶段，会随时间推移而消失，因此不予考虑。可设式（8）的特解的形式为：

其中：

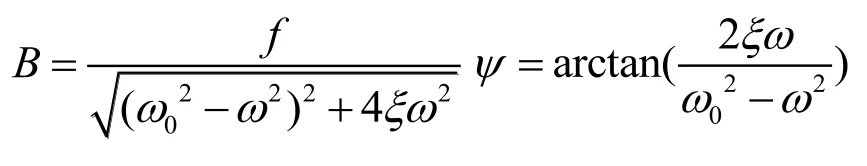
3.2 集中质量的运动为粘着时的运动方程

其中，xslip为当集中质量由滑移变为粘着时的临界点所对应的位移，t为粘着段对应的时间区间的长度。

3.3滑移—粘着临界时刻的

当滑移和粘着的运动方程分别确定后，集中质量的时域位移响应可在滑移、粘着段分段可导，因此，求解滑移—粘着—滑移变化的临界时刻就十分重要。当集中质量的速度 时，系统由滑移变为粘着，因此可将 作为判断临界时刻的标准。

本文采取变步长法，求解滑移—粘着的临界时刻，图5为计算程序的流程图。集中质量处于粘着的时间与处于滑移的时间之和为周期的一半，因此粘着—滑移转变的临界时刻可由此确定。

3.4 系统幅频响应的求解方法

由于双折线本构关系Z (t)为非线性的泛函，其示意图如图6所示，造成直接求频响方程十分困难，因此考虑Z (t)的简化形式。

双折线迟滞模型的阻力具有周期性，且没有第一类间断点，并绝对可积，因此，可将其阻力展开成Fourier级数。

如图7所示，可将双折线迟滞模型的阻力分段表示：

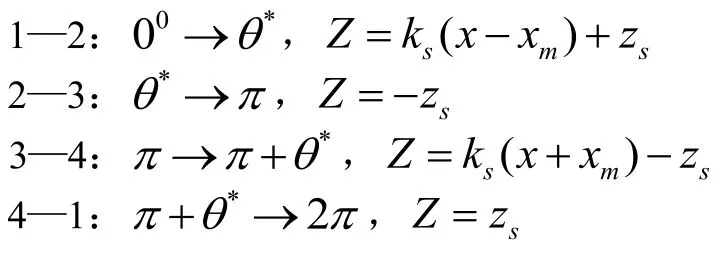
在2处，1—2与2—3分别表示的分段函数应连续，可得：

图5 临界时刻计算流程图

图6 双折线示意图

xy为双折线本构关系的滑移极限。所以，利用分段积分定理，可得阻力F的Fourier级数为：

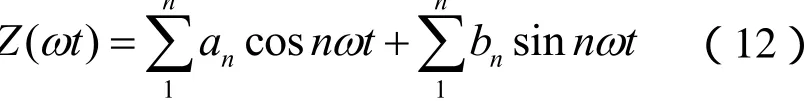
其中：

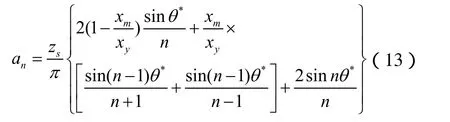
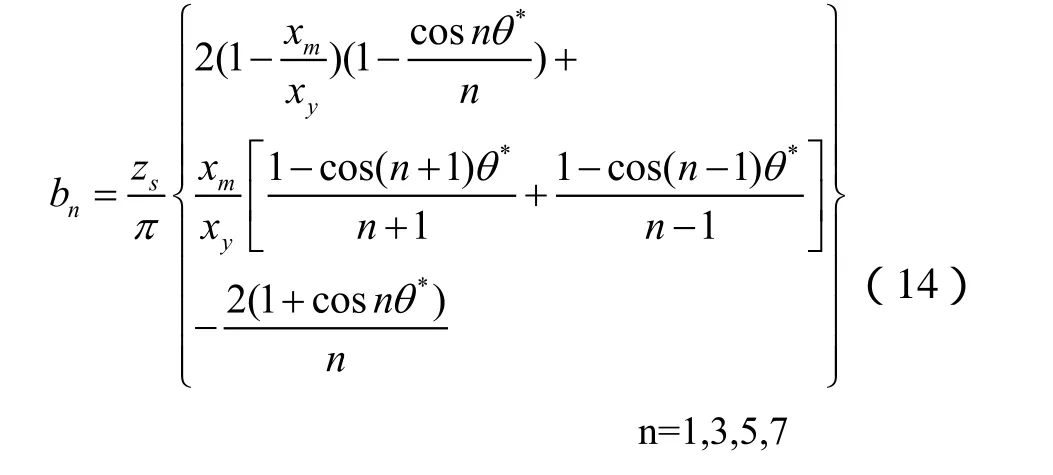
以往的文献曾对式（12）进行频谱分析，指出，式（12）中的高次谐波位移与基频位移之比均低于5.5%，甚至往往低于1%。因此，可取式（13）中n=1的各项来近似代替双折线迟滞模型的阻力。

当n=1时，简化后可得：

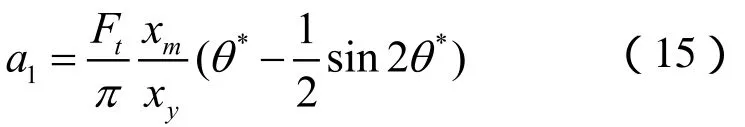
因此，双折线迟滞模型的等效阻力为：

将式（13）代入式（1）中，再对式（1）进行傅里叶变换，经整理、简化后最终可得：

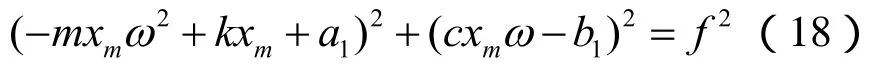
其中，xm为集中质量位移响应的幅值，利用Newton迭代法求解非线性方程（18）即可得到集中质量的幅频响应曲线。

4 计算结果及分析

为分析不同的系统参数对集中质量粘滑运动的影响，在幅值为20N，频率为5HZ的简谐激励下，分别计算了不同参数时系统的时域位移响应。系统的各参数如表1所示。

表1 系统参数

4.1 时域响应

为分析不同的系统参数对集中质量粘滑运动的影响，在幅值为20N，频率为5HZ的简谐激励下，分别计算了不同参数时系统的时域位移响应。系统的各参数如表1所示。图7为集中质量的位移响应。由图7可见，文中的计算方法可表征集中质量的粘滑运动，且带速的大小对位移的幅值有影响，带速增大时位移的幅值增大。

4.1.1 不同阻尼时集中质量的位移响应

图8为集中质量的位移响应，由图8可见，阻尼的大小对位移的幅值有影响，带速增大时位移的幅值减小。

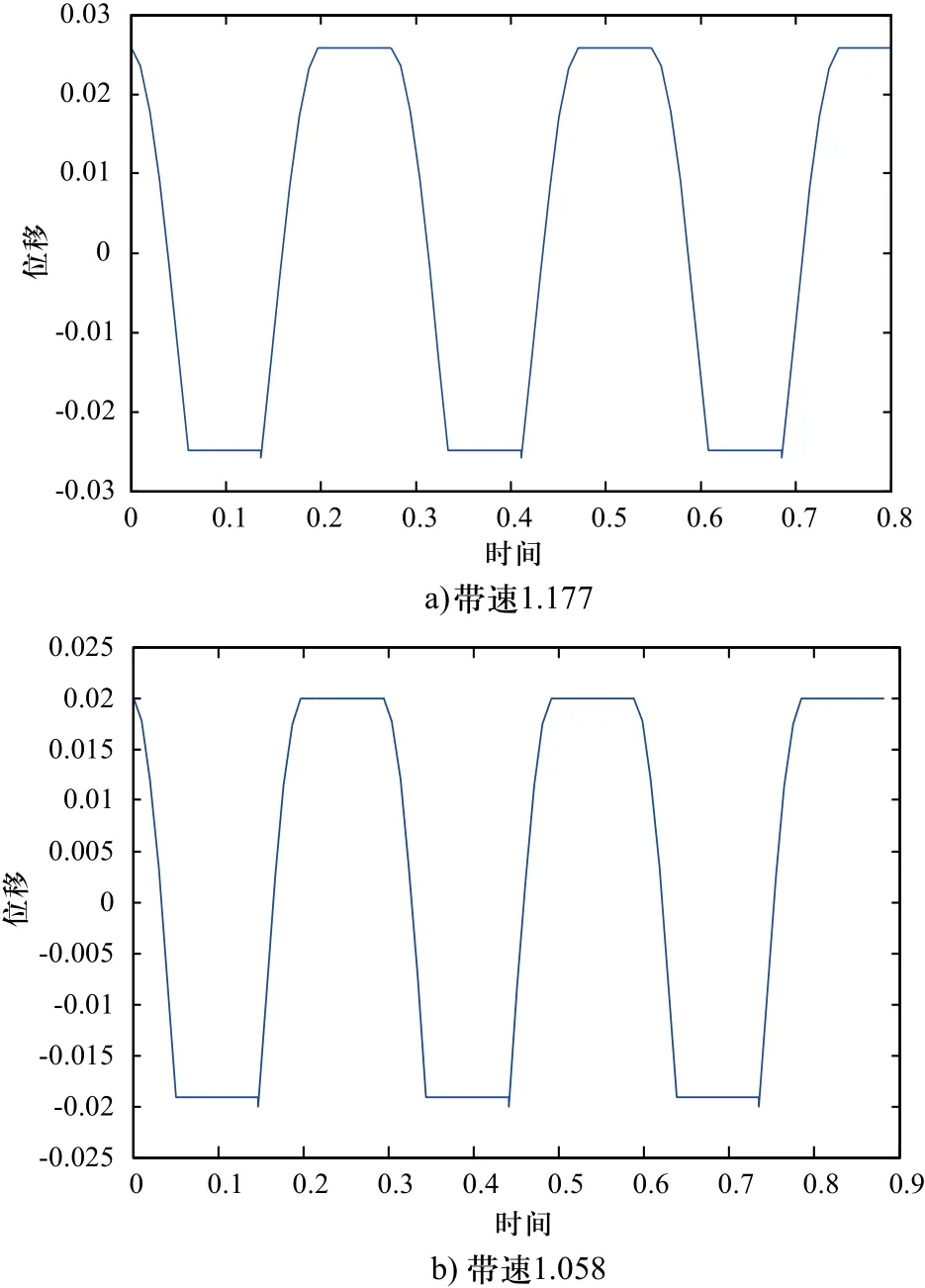
图7 集中质量位移响应

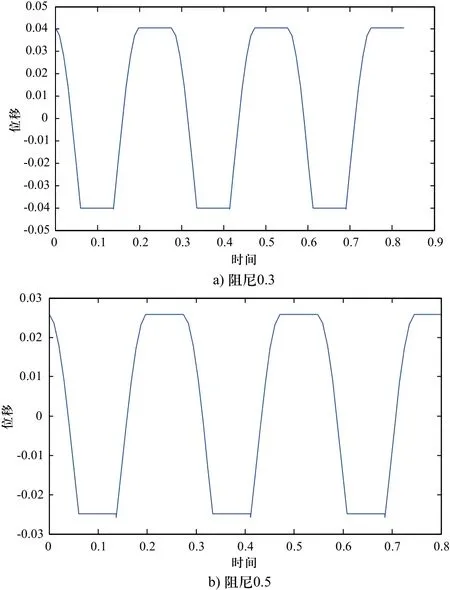
图8 集中质量位移响应 (m=0.5，k=10，zs=20，ks=25)

图9 集中质量位移响应 (c=0.5，m=0.5，zs=20，ks=25)

4.1.2 不同刚度时集中质量的位移响应

由图9可见，刚度k的大小对位移的幅值有影响，k增大时位移的幅值减小。

4.2 幅频响应

取系统参数为 m=0.05，c=0.5，k=25，zs=20，ks=22，在幅值为30N，频率为0～10HZ扫频的激励下，计算集中质量的幅频响应，结果如图10所示。可见当激励频率为5.1HZ左右时，幅频响应达到峰值。

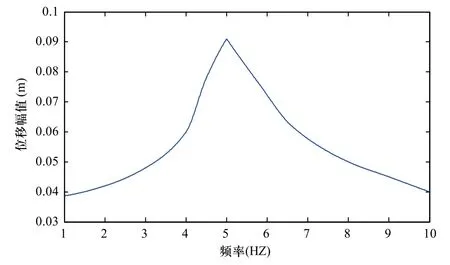
图10 集中质量的幅频响应曲线

5 结论

文中给出了干摩擦系统的建模及计算方法，分析了干摩擦系统中的参数对系统响应的影响，结果表明，文中的建模和数值方法是有效的，可供干摩擦设计借鉴。

[1] Den Hartdog,Forced vibration with combined coulomb and viscous friction[J]. Trans ASME, 1931: APM-52-15.

[2] Iwan W.F. The dynamic response of the bilinear hysteretic system [D]. Califonia: Califonia institute of technology,1961.

[3] 胡海岩, 李岳峰. 具有记忆特性的非线性减振器参数识别[J]. 振动工程学报, 1989, 2(2): 17-26.

[4] 李冬伟, 白鸿柏, 杨建春, 等. 非线性迟滞系统建模方法[J]. 机械工程学报, 2005, 41(10): 205-210.

[5] 路纯红, 白鸿柏, 胡仁喜. 金属橡胶/橡胶复合叠层耗能器动力学模型[J]. 振动工程学报, 2008, 21(5): 493-497.