一类需求不确定闭环物流系统的模糊规划模型与仿真

徐家旺，徐国慧，张 毅

(1.沈阳航空航天大学经济与管理学院，沈阳 110136;2.中国科学院沈阳自动化研究所，沈阳 110016;3.辽宁中晨市政工程有限公司，沈阳 110000)

从物流角度讲，闭环物流实质上是通过产品的正向交付与逆向回收再利用，使“资源—生产—消费—废弃”的开环过程变成了“资源—生产—消费—再生资源”的闭环反馈式循环过程。从技术上讲，闭环物流包括正向物流和逆向两部分。正向物流是一种常见的物流形式，是原材料经过一系列制造加工形成最终产品，再由分销商将其交付给顾客以满足他们需求的过程;逆向物流则是将顾客使用过的废旧产品或原材料经回收、再制造等加工处理，以充分利用其经济价值的过程［1－5］。

正向与逆向物流模型的集成称之为闭环物流模型，目前还很少有研究考虑这个问题。Fleischmann等［6］通过综合考虑没有加工能力限制的正向物流和逆向物流，设计了一个逆向物流网络，Salema等［7］对此逆向网络模型进行了扩展，提出了一个更一般的模型并将其运用于一家伊比利亚的公司，此模型考虑了加工能力有限、产品多样、需求不确定并且有废旧品回收的更一般的逆向物流网络设计问题。然而，这两个模型都没有考虑供应商以及正向物流和逆向物流之间的联系等问题。

事实上，在实际的物流系统中，顾客的需求、成本、提前期、产品质量等都是不确定的。因此，在研究物流运作管理研究时，必须要考虑如何来描述这些不确定性因素，并需要研究这些不确定性因素是如何影响物流运作策略的。从现有的相关文献看，人们通常采用概率分布、模糊集和情景集等3种方法来描述不确定性［8－11］。此外，Dimitris和Melvyn将不确定性描述为对称有界区间，并提出了一套线性鲁棒公式［12］。最近，Wang和Hsu［13］研究了正向物流与逆向物流集成问题，建立了一个线性闭环物流规划模型。然而，此模型仅考虑了一个阶段并且没有考虑整个产品的生命周期。通过改进文献［13］中所提出的闭环物流系统框架，Jia等［14］采用基于情景分析的鲁棒优化方法建立了需求是不确定的、多供应商、多制造商、多分销商、多顾客组成的多层闭环物流系统运作模型。采用具有已知概率的离散情景描述不确定性虽然简单但难以涉及闭环物流系统实际运作中不确定性存在的每一种情况，而且基于情景分析的鲁棒优化方法会在建模过程中增加大量的约束条件，使模型变得非常大，计算起来非常困难。鉴于此，本文在文献［14］的基础上，采用模糊集描述需求的不确定性，考虑如图1所示闭环物流系统的运作问题，建立该系统的模糊规划模型，并通过仿真算例来验证所建立的模糊规划模型的有效性。

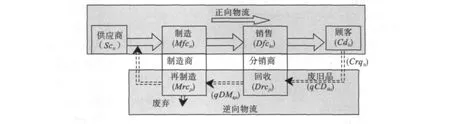
图1 闭环物流系统的结构框架

1 符号与假设

1.1 符号

下标:i—供应商(i=1，2，...，I);j—制造商(j=1，2，...，J);k—分销商(k=1，2，...，K);l—顾客(l=1，2，...，L);t—阶段(t=1，2，…，T)。

参数:Scit— 阶段 t供应商 i的供应能力;Mfcjt—阶段 t制造商 j的正向物流处理能力;Mrcjt—阶段t制造商j的逆向物流处理能力;Mvit—制造商j采用供应商i提供的原材料进行生产时的单位生产成本;Mfj—制造商j运营的固定成本;MDvjk—制造商j到分销商k的单位运输成本;Dfckt—阶段t分销商k的正向物流处理能力;Drckt—阶段t分销商k的逆向物流处理能力;DCvkl—分销商 k到顾客 l的单位运输成本;DMvkj—分销商k到制造商j的单位运输成本;Dfk—分销商k运营的固定成本;Cdlt—阶段t顾客l的需求;Crqlt—阶段t顾客l的废旧物品回收数量;CDvlk—分销商k从顾客l处回收废旧品的单位成本;Lfj—制造商j处理废旧品的单位成本;γjt—阶段t制造商j废旧品废弃率。

决策变量:qfMijt—阶段t制造商j利用供应商i供应的原材料生产的产品数量;qrMjt—阶段t制造商j的再制造量;qlMjt—阶段t制造商j再制造时的废弃量;qMDjkt—阶段t制造商j运往分销商k的产品数量;qDCklt—阶段t分销商k销售给顾客l的产品数量;qDMkjt—阶段t分销商k运往制造商j的废旧品数量;qCDlkt—阶段t分销商k从顾客l处回收的废旧品数量。

1.2 假设

建模过程中，图1所示系统需满足下列条件:(1)所有顾客的需求都是不确定的，并可用模糊集描述;(2)物流仅能在2个相邻的层级之间流动;(3)废旧产品的回收率和废弃率都是已知的;(4)再制造的延迟时间为τ;(5)产品的生命周期为T－τ，在生命周期中的废旧概率为μp(p=1，2，…，T － τ)，且=1;(7)阶段 t顾客 l处的回收率为ηlt。

2 模 型

在图1所示的闭环物流系统运作过程中，顾客的需求是不确定的。一般情况下，不确定性可用一个区间来表示，为了分析方便，在此将顾客的不确定性需求Cdlt的波动范围描述为［Cdlt，Cdlt+ΔCdlt］。其中，ΔCdlt是已知的非负常数，为 Cdlt的伸缩度，标志顾客需求的不确定性程度。令ΔCdlt=ρ% ×Cdlt，通过改变ρ的值来表示不同的伸缩度，即不确定性程度。

令μlt为阶段t顾客l的需求未满足量，plt为未满足需求的单位惩罚。在图1所示的闭环物流系统运作过程中，追求运输总成本、开工运营总成本以及所有未满足需求的惩罚之和为最小，则系统的运作目标函数可以表示如下:

其中，∑t∑i∑jMvij×qfMijt为制造商利用供应商供应的原材料制造新产品的总费用;∑t∑j∑kMDvjk×qMDjkt为将产品从制造商运往分销商的总运输费用;∑t∑k∑jDMvkj×qDMkjt为分销商将回收的废旧品运往制造商的总费用;∑t∑jLfj×qlMjt为制造商处理再制造后遗留废弃物的总固定费用;∑t∑jMff×αjt为制造商的运营固定费用;∑t∑kDfk× βkt为分销商的运营固定费用;∑l∑tplt×ult为顾客需求得不到满足时的处罚;∑t∑k∑lDCvkl×qDCklt为分销商将产品运往顾客的总运输费用;∑t∑l∑kCDvlk×qCDlkt为分销商回收废旧品的总费用。

为了建立系统运作的模糊规划模型，将以上的目标模糊化后得到目标的隶属函数:

其中，TCmin和 TCmax应满足 TCmin≤ TC≤TCmax，它们是决策者根据实际情况给出的总成本费用TC的最小期望值和最大期望值。当然，在实际运用时，也可以参照对应的确定数学规划问题的最优解给出TCmin和TCmax的具体估计值。

图1所示系统的运作受到如下几个条件的约束［14］。

供应商原材料供应能力约束:

制造商正向物流加工能力约束:

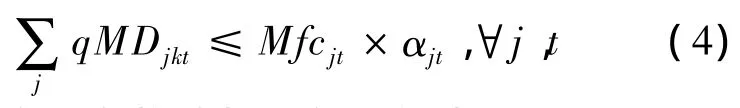
制造商逆向物流加工能力约束:

分销商正向物流处理能力约束:

分销商逆向物流处理能力约束:

制造商物流的流入与流出平衡约束:

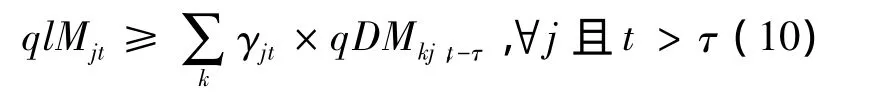
分销商处物流的流入与流出平衡约束:

尽量满足顾客的需求

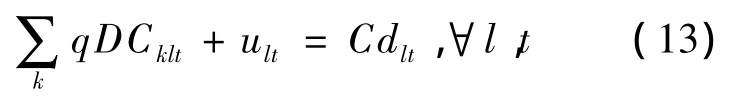
由于以上约束条件中带有不确定性参数Cdlt，因此需要将其模糊化，得到以下的隶属函数:

顾客处产品废弃与回收之间的关系:

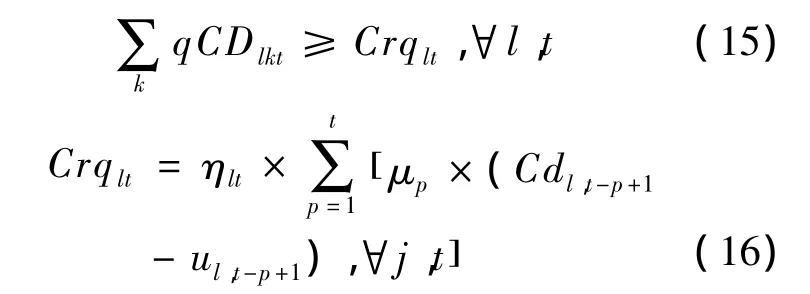
0－1变量:

非负、整数条件:

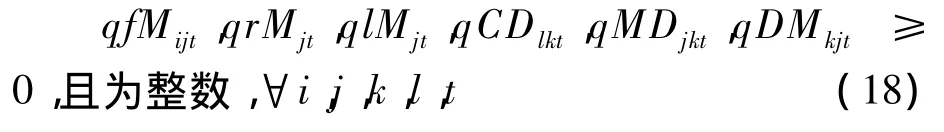
以上所建闭环物流系统运作模糊规划模型中包含了隶属函数，为了求解方便，在此根据模糊数学原理［15］，将以上的模糊规划模型转化为如下的混合0－1整数线性规划问题。

目标函数:

min λ

其中0≤λ≤1。

约束条件:

其中，TC如式(1)所示。

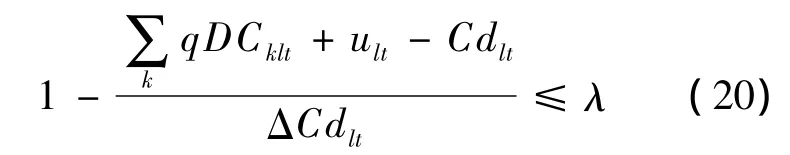
其他的约束条件还包括不含不确定性参数的约束条件(3)－(12)、(15)－(18)。

3 仿真分析

考虑由3个供应商、5个制造商、3个分销商和4个顾客构成的4阶段闭环物流系统。根据历史资料得到的各阶段所有顾客平均需求(需求确定情形)如表1所示。分销商从顾客处回收废旧品的单位成本以及制造商运用不同供应商供应的原材料制造产品的单位可变成本如表2所示，供应商、制造商、分销商各阶段的加工处理能力、运营固定成本以及它们之间的单位运输成本分别如表3和表4所示(其中的一些数据来源于文献［13］，并假定以上参数值在4个阶段均相同)。

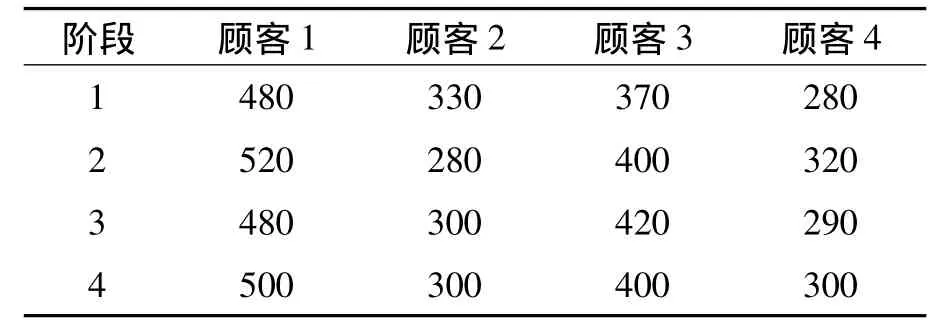
表1 顾客的平均需求

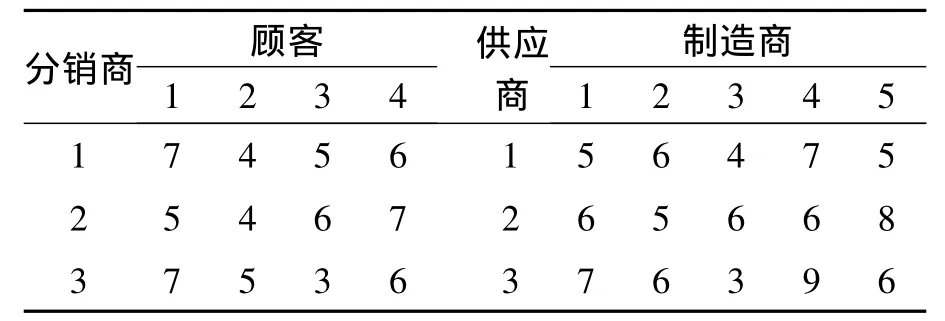
表2 可变成本

表3 加工能力及运营固定成本

表4 单位运输成本

产品的生命周期P=4，生命周期内产品废旧的概率分别为 μ1=0.1，μ2=0.2，μ3=0.3，μ4=0.4，废旧品再制造延迟τ=0，各阶段顾客废旧产品回收率均为60%(即ηlt=60%，∀l，t)，且顾客需求未得到满足时，每单位的处罚均为100(即plt=100，∀l，t)，所有制造商处理废旧品的单位成本均为5(即Lfj=5，∀j)。

根据以上给定的参数值，采用优化建模软件LINGO9.0，针对几种不同的运作情形对所建模糊规划模型进行了仿真模拟，得到的具体结果如下。

(1)当需求是确定的时候，需求量取表1所示的平均需求值，通过计算得到仿真模型的目标函数值为119908，系统各阶段的运作策略如表5所示。

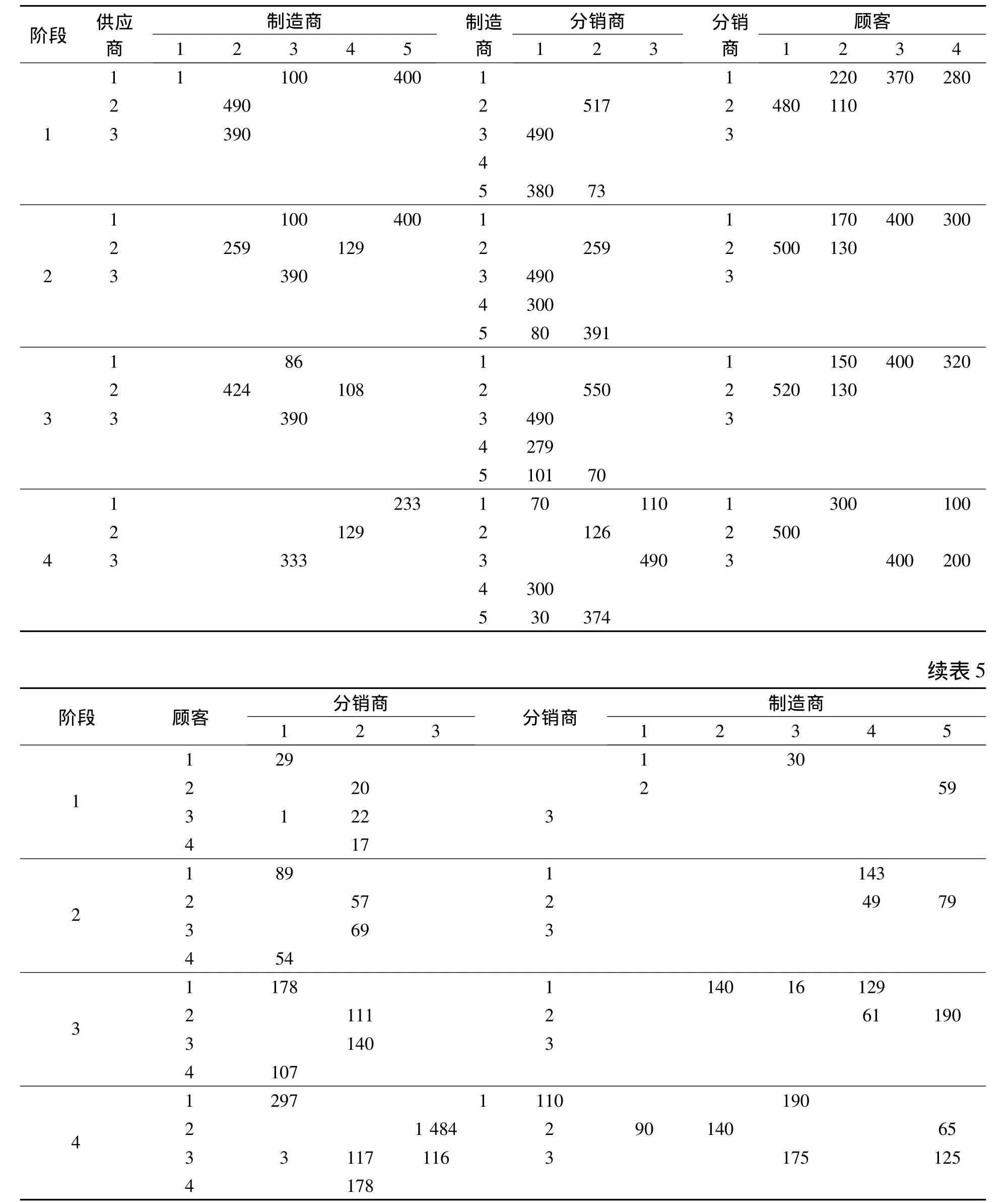
表5 需求确定情形系统的运作策略

从表5可以看出，在前3个阶段，制造商1和分销商3均不需要开工，制造商1仅在第4阶段运营，且仅加工废旧产品即进行再制造，顾客的所有需求全部得到了满足。同时可以发现，随着时间的推移，从顾客处回收的废旧产品逐渐增多，制造商从外部供应商处购买原材料制造新产品的数量逐渐减少。从以上的仿真结果可以看出，模型能够很好地从经济学角度为绿色供应链管理服务。

(2)当需求是不确定的时候，利用以上所给定的参数值，取伸缩度ρ为20，即需求的波动区间为［Cdlt，1.2×Cdlt］。通过计算可得，此时仿真模型的目标函数值为146148，系统各阶段的运作策略如表6所示。

表6 需求不确定情形(ρ=20)时系统的运作策略

与需求确定时的情形相似，制造商1在4个阶段均不制造新产品，仅在第4阶段利用回收的废旧产品进行再制造;分销商1在第1和第2阶段既不销售新产品也不回收废旧产品，即不运营，这样能够节约不少的固定运营成本。随着时间的推移，从顾客处回收的废旧产品逐渐增多，制造商从外部供应商处购买原材料制造新产品的数量逐渐减少。除了在第2阶段顾客1和顾客4的需求满足量低于平均需求外，其他任何阶段任何顾客的需求满足量均超过了平均需求量，因此，在需求不确定情况下，分销商需付出比较大的需求过量风险。

(3)一般地，在模型的实际应用过程中，需求的波动区间可以通过历史资料估计出来。在此，我们利用所建模型计算了需求不确定伸缩度ρ分别取 0、5、10、15、20、25、30、35、40、45 和 50 共 11个不同值时的目标函数值和运作策略。表7列出了ρ取不同值时的目标函数值。

表7 取不同值时的目标函数值

从表6和表7可以看出，顾客需求不确定时，无论需求波动的范围有多大，系统中的各成员均需付出比较大的需求过量风险。模型的最优目标函数值说明，需求不确定时，系统的总成本均会较需求确定时的值有不同程度的增加，但从表7的数据看来，在需求不确定伸缩度的ρ值不超过50时，总成本的增加量最大不会超过确定时总成本的25%。利用该模型所得的最优运作策略，决策者可以根据顾客需求的不确定性程度来做出最佳决策方案。

4 结束语

基于早期的研究结果，设计了一个新的闭环物流系统。在此系统中，废旧品的回收由分销商完成，制造商同时进行制造和再制造，同时顾客的需求是不确定的。本文采用模糊集将不确定性需求描述为一个模糊区间，建立了该系统的模糊规划模型，并利用仿真算例验证了模型的可用性。仿真算例的结果表明，虽然需求的波动会使系统的总成本较需求确定时的值有不同程度的增加，但决策者仍可以根据顾客需求不确定程度来做出最佳决策方案。

［1］ Ko H J，Evans G W.A genetic algorithm －based heuristic for the dynamic integrated forward/reverse logistics network for 3PLs［J］.Computers＆ Operations Research，2007，34(2):346 －36.

［2］ Pishvaee M S，Farahani R Z，Dullaert W.A memetic algorithm for bi－objective integrated forward/reverse logistics network design［J］.Computers＆ Operations Research，2010，37(6):1100 －1112.

［3］ Fleischmann M，Bloemhof－ Ruwaard J M，et al.Quantitative models for reverse logistics:a review［J］.European Journal of Operational Research，1997，103:1－17.

［4］ Lu Z Q，Bostel N.A facility location model for logistics systems including reverse flows:the case of remanufacturing activities［J］.Computers＆ Operations Research，2007，34(2):299 －323.

［5］ de la Fuente M V，Ros L，Cardós M.Integrating forward and reverse supply chains:application to a metalmechanic company［J］.International Journal of Production Economics，2008，111(2):782 －792.

［6］ Fleischmann M，Beullens P，Bloemhof－Ruwaard J M，et al.The impact of product recovery on logistics network design［J］.Production and Operations Management，2001，10(2):156 －173.

［7］ Salema M I G，Barbosa－Povoa A P，Novais A Q.An optimization model for the design of a capacitated multi－product reverse logistics network with uncertainty ［J］.European Journal of Operational Research，2007，179(3):1063 －1077.

［8］ Liu M L and Sahinidis N V.Process planning in a fuzzy environment［J］.European Journal of Operational Research，1997，100:142 －169.

［9］陈红萍，杜健邦，穆东.基于供需不确定的供应链FUZZY规划模型分析［J］.物流技术，2010(2):155－158.

［10］阮家港，扶秀红.模糊需求与模糊提前期易逝品供应链渠道协调的数量折扣契约研究［J］.科技与管理，2011，13(4):73 －77.

［11］莎娜，季建华，陈祥国.供应链不确定性的情景分析探讨［J］.情报杂志，2011，30(2):194 －198.

［12］Dimitris B，Melvyn S.The price of robustness［J］.Operations Research，2004，52(1):35 －53.

［13］Wang H F，Hsu H W.A closed －loop logistic model with a spanning－tree based genetic algorithm［J］.Computers ＆ Operations Research，2010，37(2):376－389.

［14］Jia H L，Xu J W，Sun Z F.An optimization model for closed－loop logistic system with uncertain demands［C］.Proceedings of the 29th Chinese Control Conference，2010:1201 －1206.

［15］Yang Z Z，Yu B，Cheng C T.A parallel ant colony algorithm for bus network optimization ［J］.Computer-Aided Civil and Infrastructure Engineering，2007，22:44－55.