基于模糊距离变换的骨架剪枝算法

张国栋，韩佳池

(沈阳航空航天大学计算机学院，沈阳 110136)

骨架作为一种简单的物体形状表示方式，不仅结合了物体的轮廓和区域信息，同时反应了物体重要的视觉信息，能够方便的实现物体的特征匹配。基于骨架的目标表示和识别技术是模式识别和计算机视觉的重要研究内容，被广泛的应用于字符识别、指纹识别及医学图像分析等领域。

目前最具代表性的骨架定义主要有两种。一种是火烧1模型(Grassfire)，该模型假设物体边界点上的火源同时向内燃烧，火焰成等距同心圆向内推进，两圆的切点就是物体的骨架点。细化法(Thinning)是模拟烧草模型的典型代表。传统的细化算法能够很好的保证骨架的连通性，但不能保证骨架点的准确性。另一种是最大圆定义法(maximal disk)，将骨架定义为物体内最大圆圆心的集合［1］。基于距离变换的骨架提取算法就是利用最大圆的理论，将任意点的距离变换值作为圆的半径，比较所有内切圆的包含关系最终找到最大圆的圆心。基于距离变换的骨架算法能够保证骨架的正确位置，确保骨架的拓扑结构，但缺点是不能保证骨架的连通性。典型的骨架生成算法无法避免的导致骨架产生过多的毛刺状分枝，通常都需要一些后期的处理，因此骨架剪枝技术就成为一种辅助需要［2－3］。

模糊距离变换结合了距离变换与模糊理论的双重特点，因此同距离变换一样模糊距离变换也能够反应物体的中轴信息。与此同时，由于模糊距离变换是对灰度图像的操作，同时考虑了图像的灰度信息和位置信息，因此相较于距离变换来说具有更强的稳定性，并且能够加精确的反应物体骨架点位置。对于边界模糊的物体不再需要对其进行二值化操作，在处理模糊图像时这一特性解决了难于对模糊图像二值化的问题。通过以上分析可以发现，使用模糊距离变换值作为衡量骨架分支重要程度的标准，可以实现对物体粗骨架的剪枝操作。

本文提出的剪枝算法依据模糊距离变化这一理论基础，在物体粗骨架图中计算与骨架点相对应的模糊距离变换值，利用模糊距离变换值作为骨架分枝的显著性度量标准，选取有效的剪枝阈值，通过分级剪枝操作去除骨架中的毛刺。

1 算法基本理论

1.1 基于模糊理论的模糊距离变换

距离变换作为一种有效的方法被广泛的应用于目标识别和图像处理领域。距离变换是针对二值图像的操作，表示目标点到距其最近背景点的距离。由于距离变换的定义无法有效的应用于模糊对象中，因此我们将在模糊对象中的距离变换称作模糊距离变换［4］。模糊距离变换是对灰度图像的操作，它同时考虑了图像的灰度信息和距离信息。模糊距离变换通过引入一个隶属度函数，拓宽了距离变换的应用范围，使其可以用于解决模糊对象问题。模糊距离变换(fuzzy distance transform，FDT)是模糊子集上的一个路径长度，是两点之间所有路径长度的最小值［5］。下面给出模糊距离变换在数字网格空间中的定义和实现算法。

定义1(隶属度函数)设X是一个集合，S是X的模糊子集，则S是一个有序对集合，S={(x，μs(x))|x∈X}其中 μs(x):X→［0，1］是集合 S 的隶属度函数。

定义2(支持域)o描述模糊分割后的目标物体，目标物体o的支撑域Θ(O)是所有隶属度函数值不为零的像素的集合，如公式(1)所示。

定义3(链接)相邻两点p和q之间的长度定义为链接〈p，q〉，链接〈p，q〉的长度如公式(2)所示。

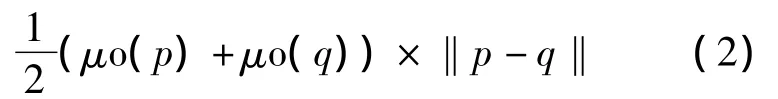
定义4(路径)在集合S中，点p∈S到点q∈S的路径 π 是一个连续序列，〈p=p1，p2，…，pm=q〉其中 pi∈S，1≤i≤m，对于任意的1≤j≤m，pj与pj+1是邻接关系。

定义5(路径长度)路径 π=〈p=p1，p2，…，pm=q〉的长度记为Πo(π)，是路径π上所有链接的和，如公式(3)所示。

假设P(p，q)表示p点到q点间所有路径的集合，对于任意的路径 π∈P(p，q)，如果满足 Πo(πp，q)≤Πo(π)，则称 πp，q∈P(p，q)是 p 点到 q点的一条最短路径。用ωo(p，q)表示p点到q点的模糊距离，即从p到q的最短路径的长度，如公式(4)所示。

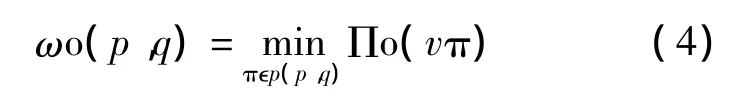
定义6(模糊距离)在数字空间中，Ωo(p)表示模糊对象中p点的模糊距离变换值，是p点到距其最近的背景点的模糊距离，如公式(5)所示。

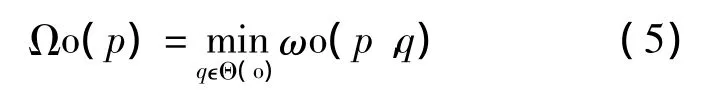
本文使用Punam K.Saha提出的动态规划方法计算物体的FDT值。

1.2 骨架中点的类型

实现骨架剪枝算法的关键之一在于找到骨架的各个分枝。骨架中的每个分枝都是由骨架上的点组成，因此分清骨架中点的类型则变得极为重要。骨架中的点主要分为3种，即端点、节点和一般点。其中一般点是骨架的主要组成部分，节点和端点则出现在骨架发生剧烈变化的地方，他们反应了骨架主要的拓扑变化。将节点和端点统称为特殊骨架点。下面给出骨架点的具体描述。

对于任意骨架点p的8－邻域范围内仅存在一个骨架点时，我们称它为端点。端点标识骨架每个分支的起点。对于任意的骨架点p的8－邻域范围内存在至少两个骨架点时，我们称它为节点。节点是骨架不同部分的交汇点。若节点的8－邻域范围内存在3个骨架点且任意两个骨架点不相邻，则此节点有3个分枝，称p为三分枝节点。如果任意的节点p存在至少两个尾枝，则称它为多尾枝节点。去除端点和节点后，骨架中其它点的8－邻域范围内存在两个骨架点，我们称他们为一般点。

骨架的一般点构成的连通集合称为骨架段。由定义可以看出骨架中大部分的点都是一般点。连通任意两个特殊骨架点且不通过第3个特殊骨架点并且具有惟一连通通路的骨架段称为骨架的分枝。将节点与节点之间的骨架称为一般分枝，将节点与端点之间的骨架称为尾枝。由任意端点可以惟一的确定一条尾枝。将由同一节点引出的多个尾枝中不符合条件的尾枝称为毛刺。将非毛刺的尾枝称为一般尾枝。

2 算法实现

2.1 算法基本原理

本文提出的基于模糊距离变换的骨架剪枝算法，在对模糊距离变换图像成像特点分析的基础上，在粗骨架中使用模糊距离变换值作为骨架点的权值，按照规定的剪枝规则和设定的剪枝阈值，实现对粗骨架图像进行分级的骨架剪枝操作，最终得到只反映物体主要拓扑结构的骨架。

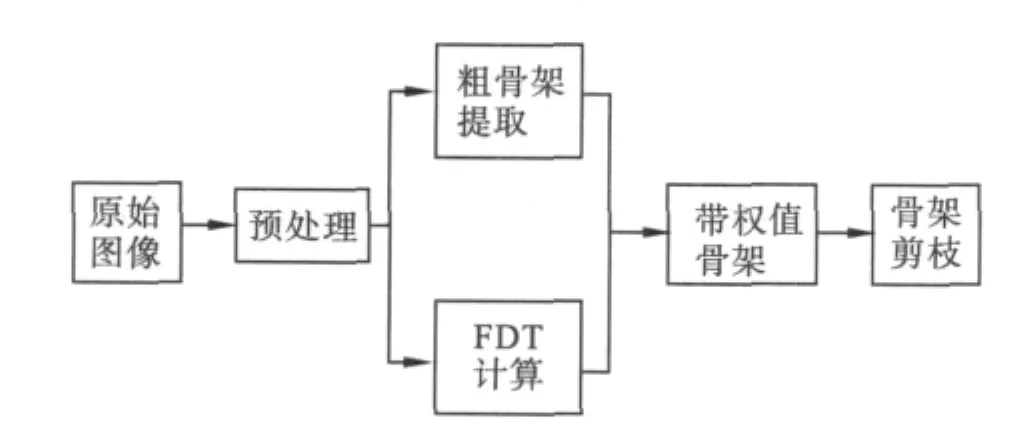
图1 算法流程

图1给出了该算法的基本流程。首先对原始图像做去噪声、计算隶属度等预处理;然后使用动态规划算法对预处理后的图像进行模糊距离变换操作，同时使用现有的形态学骨架提取算法获得目标物体的粗骨架图像;接下来结合上一步骤所得到的粗骨架图像和模糊距离变换图像获得带权值的骨架图;最后结合骨架的最小尾枝权值和当前尾枝权值确定动态剪枝阈值，并结合分级的剪枝规则实现剪枝操作。

2.2 算法描述

2.2.1 骨架权值计算

通过模糊距离变换我们得到了一个标量场，即模糊距离变换场。按照骨架的最大圆定义可以发现模糊距离变换与骨架之间有着某种联系［6］，骨架点处的模糊距离变换值比其大多数相邻点的模糊距离变换值要大。因此，利用模糊距离变换值作为骨架分枝的权值，对粗骨架进行剪枝操作将会得到良好的效果。在计算图像的模糊距离变换时使用1.1节中所介绍的距离计算公式和实现方法，选取高斯函数为隶属度函数，如公式(6)所示。

其中f是图像灰度函数，mA和σA分别是灰度的平均值和标准差，Gma，σA是未规范化的高斯函数。

图2(a)为由彩色图像得到的灰度图，图2(b)表示了图2(a)中物体的模糊距离变换，亮色处表示数值较大的位置，图2(c)为利用matlab自带函数bwmorph得到的物体粗骨架图。从图2(b)中可以看到，模糊距离变换图像的脊线能够精确的表示物体的拓扑结构。从图2(c)中我们可以看到，由函数bwmorph得到的骨架中，除了能够反应物体拓扑特征的关键分枝外，在每条关键分枝上还存在很多细小的多余分枝，这些多余分枝会直接影响后续目标识别和特征提取等操作的效果及正确性。这里我们使用模糊距离变换作为剪枝权值同时结合了骨架的位置和灰度信息，与文献［3］中使用的受图像形状因素影响过大的方法相比有更好的准确性和稳定性。

图2 物体灰度图、物体FDT图、物体的粗骨架图、物体的带权值骨架图

利用粗骨架上各点对应的模糊距离变换值便可以得到带权值的粗骨架图，如图2(d)所示。具体步骤如下。

步骤1:利用bwmorph函数对图像进行骨架提取，得到粗骨架图像。

步骤2:利用动态规划法对图像进行模糊距离变换计算，得到图像的模糊距离变换图。

步骤3:合并(1)(2)得到的结果，即得到带权值的粗骨架图像，该骨架图反映了骨架的不同等级信息。

2.2.2 剪枝阈值的确定

剪枝阈值作为判断尾枝是否为毛刺的依据，对骨架的剪枝效果起到了决定性的作用。在粗骨架图中检测并标记骨架的端点和节点。从骨架的每一个端点出发，对骨架进行跟踪，直至跟踪到一个节点，得到一条尾枝，将尾枝上所有骨架点的值进行累加作为该尾枝的权值。设置一个能够反映尾枝重要程度的剪枝阈值。将尾枝的权值与剪枝阈值做比较来判定该尾枝是否是骨架的毛刺。被判定为毛刺的尾枝意味着它是由噪声或细节产生的，在目标匹配中将不予以考虑。如果被判定为一般尾枝，则说明它能够反映目标的重要形态结构，对后期工作的开展意义重大。

剪枝阈值(Ath)的选取必须能够动态的表征全局信息，并且能够体现当前尾枝的信息，这样才能保证快速、有效的实现骨架剪枝操作。设骨架中尾枝权值的最小值为 Amin，当前尾枝权值为Anow，剪枝阈值如公式(7)所示。

每次删除毛刺都会影响到Amin的值，随着剪枝次数的增加Amin的值在不断增大，说明Amin能够动态的表示骨架的全局信息，这也是我们在选取剪枝阈值时使用Amin值的主要原因。

2.2.3 骨架的分级剪枝

由于删除毛刺的同时会导致新的毛刺的产生，因此骨架剪枝不可能一步完成，必须分级进行处理，级别由小到大会导致剪枝后的骨架结构由繁到简。适度的把握剪枝级别有助于得到精确的骨架结构。级别过小会导致骨架分枝过多，无法准确的反映物体的真实结构;级别过大会导致骨架分枝过少，无法正确表示骨架的拓扑结构，最终导致错误的表现物体的形状及形态。

为了实现分级剪枝，设计如下的剪枝规则。如果节点只有一个尾枝，则将尾枝的权值与剪枝阈值做比较，若尾枝的权值小于剪枝阈值，则认为该尾枝并非是目标的结构信息，应将其作为毛刺去除，否则保留。如果节点为多尾枝节点，则需对其进行分类处理，首先将小于阈值的尾枝去除，若仍存在两条的尾枝，则比较两尾枝权值的差值与阈值的大小，找到毛刺尾枝予以去除。

每次剪枝后，骨架中端点和分叉点的信息都会改变，因此每次剪枝结束后都需要重新检测骨架中的端点和分叉点。尾枝类型的转换及骨架点的更新原则。假设由节点p引出n条尾枝，如果p的k(k＜n)条尾枝被去除，骨架的端点数减少k个，节点p变为(n－k)条尾枝节点;如果p的(n－1)条被删除，p点转化为普通的一般点，剩下的这条尾枝与节点所在的骨架段组成了一条更长的尾枝，骨架的端点数减少(n－1)个。假设从节点p只引出一条尾枝，若该尾枝是毛刺则去除，此时节点变为一般点，否则保留，骨架点信息不变。根据上述操作不难看出，每次删除毛刺都会影响到Amin的值，随着剪枝次数的增加Amin的值在不断增大，说明Amin能够动态的表示骨架的全局信息，这也是我们在选取剪枝阈值时使用Amin值的主要原因。

在某一级别处理结束之后，如果端点的数目没有变化，说明本级处理过程没有去除任何一条尾枝，此时算法收敛，终止处理过程。需要注意的是，在本算法中如果骨架比较简单，在处理级别还未达到极限处理级别时，算法就会结束。此时骨架将是一条折线，没有任何的分枝。可见，在实际应用中，针对骨架的复杂情况选取适当的处理级别是十分重要的。

3 实验结果及分析

实验中，首先对原始图像进行形态学骨架提取(使用Matlab7.0中提供的形态学骨架化函数bwmorph)，然后使用本文提出的骨架剪枝算法对形态学方法得到的粗骨架进行剪枝处理。骨架尾枝权值的计算和骨架剪枝规则按照前节介绍方法进行，剪枝从第一级别开始，直至得到最佳效果。不同的图像得到的骨架图复杂程度不同，在剪枝时所需的剪枝级别也相应的不同。

对枫叶图像进行实验，结果如图3所示，左边是试验原图像，中间是原图像通过形态学骨架算法提取的粗骨架，右边是对中间图像剪枝后的结果。可见，剪枝后的骨架正确的反应了枫叶叶片的形态结构，同时有效的去除了有细节部分所产生的小分支。

图3 图2中物体骨架提取和毛刺去除效果

图4是对同一飞机图片不同仿射变换结果进行剪枝的试验结果。左边一列为图像在不同仿射变换下的灰度图像，中间一列是不同仿射变换图像的粗骨架图像，从图4中我们可以看出，同一图像在不同的仿射变换后得到的粗骨架图是截然不同的，右边一列是应用本文算法，对粗骨架剪枝后的结果图像。

通过对图4中3组图像的对比不难看出，该算法对不同仿射变换后的复杂图像具有良好的剪枝效果。与文献［2］中提出的使用骨架权值的最大值和最小值结合得到的剪枝阈值相比较，本算法提出的剪枝阈值在剪枝操作中效率更高。表1中分析了在以上两幅图像中使用不同的剪枝阈值所需要的剪枝操作次数。

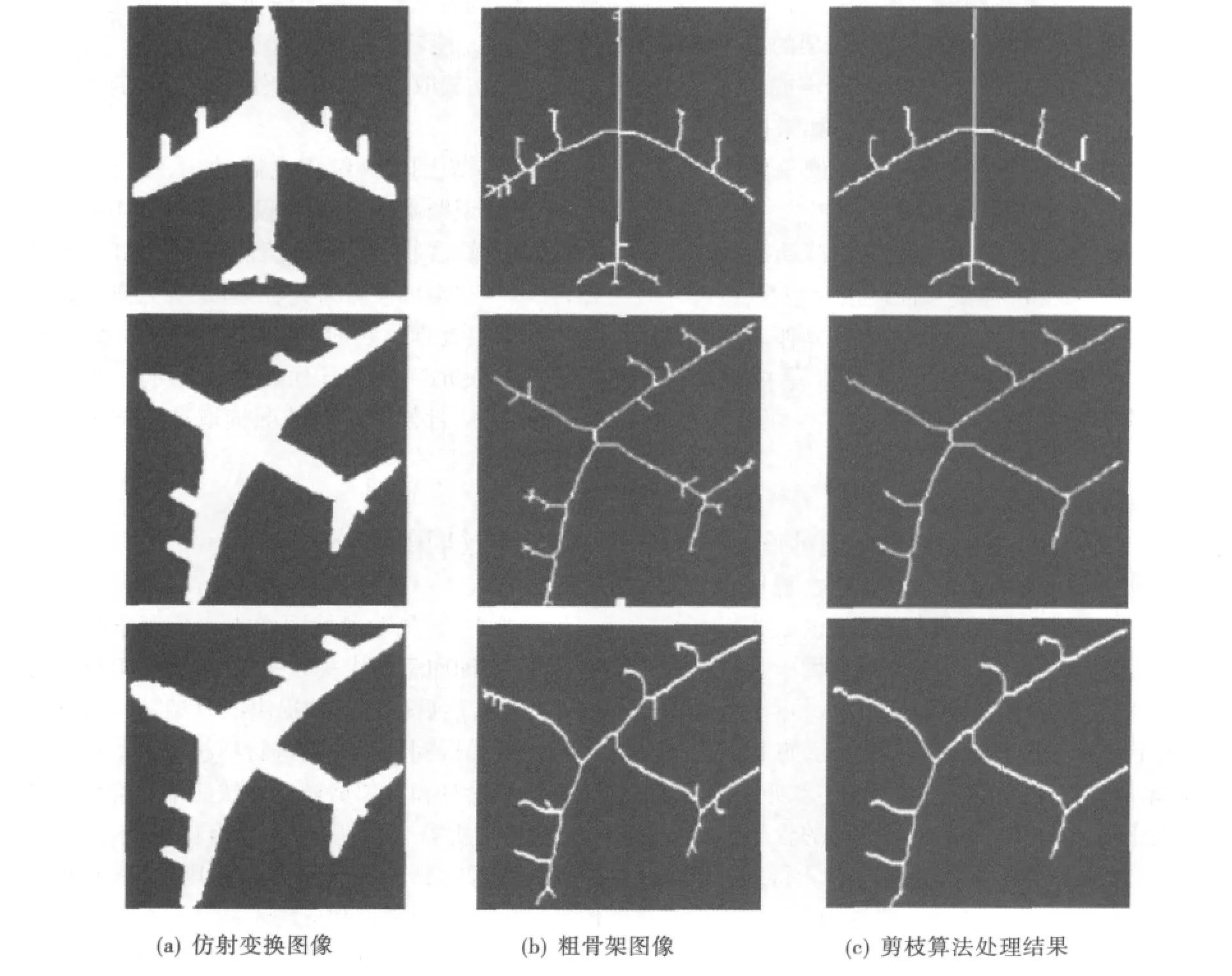
图4 同一目标仿射变换后剪枝效果

从表1可以看出，针对同一副图像，本文所使用的剪枝阈值更加能够更加快速的获得最优的剪枝结果。在处理枫叶图像时，本文算法相较于文献［2］算法节省了12次剪枝操作;在飞机图像中节省了8次剪枝操作。说明本算法在保证实验结果的同时，提高了骨架剪枝效率。

表1 本文算法与文献［2］算法剪枝次数比较

以上实验结果说明该算法能够快速、有效的去除由细节或噪声产生的多余分支和毛刺，并且能够保证较好的稳定性。

4 结束语

针对传统骨架提取方法获得的结果中出现骨架多像素及毛刺较多的现象，本文提出一种基于模糊距离变换的骨架剪枝算法。该算法依据物体的模糊距离变换值，通过比较粗骨架中各尾枝权值和剪枝阈值的关系实现粗骨架的剪枝处理。确定剪枝阈值时充分考虑其动态性，使剪枝阈值随着剪枝级别的升高而逐渐增大，使剪枝过程分级化，避免将骨架主要部分作为毛刺去除。实验结果表明，该方法实现简单、快速，能够去除骨架中多余的分支，同时保证了骨架结构的稳定性。通过对物体模糊距离变换图像的分析，发现物体的骨架线恰好在模糊距离变换图像的脊线上，由此将其应用于骨架剪枝操作中，根据这一特性，可以考虑在后期研究中利用模糊距离变换图像中局部较大的值直接对物体进行骨架提取，用这种方法得到的骨架将会比利用形态学方法得到的骨架更加精确，且不再需要后期的剪枝操作。

［1］丁颐，刘文予，郑宇化.基于距离变换的多尺度连通骨架算法［J］.红外与毫米波学报，2005，24(4):281－285.

［2］李小燕，程显毅.基于权值的骨架修剪算法［J］.计算机工程与设计，2009，30(14):3374 －3376.

［3］秦筱楲，蔡超，周成平.一种有效的骨架毛刺去除算法［J］.中华科技大学学报(自然科学版)，2004，32(12):28－31.

［4］ Punam K.Saha，Felix W.Wehrli，Bryon R.Gomberg.Fuzzy distance transform:theory，algorithms and applications［J］.Computer Vision and Image Understanding，2002，86(3):171 －190.

［5］许燕，Punam K.Saha，胡广书，等.基于模糊距离变换的三维血管造影冠状动脉形状分析［J］.清华大学学报(自然科学版)，2010，50(3):454 －457.

［6］ Stina Svensson.Centres of maximal balls extracted from a fuzzy distance［R］.Proceedings of 8th International Symposium on Mathematical Morphology(ISMM 2007)in Pio de Janerio，Brasil，Oct.10 － 13，2007.

［7］刘俊涛，刘文予，吴彩华，等.一种提取物体线形骨架的新方法［J］.自动化学报，2008，34(6):617 －622.

［8］王金玲，段会川，刘弘.基于轮廓线度量的形态学骨架剪枝方法［J］.计算机工程与设计，2009，30(9):2283－2285.