基于半参数化SLC的雷达目标识别

崔姗姗 周建江 朱劼昊

(南京航空航天大学电子信息工程学院 南京 210016)

1 引言

高分辨距离像(High-Resolution Range Profile,HRRP)是宽带雷达信号获取的目标散射点子回波在雷达视线方向上投影的矢量和，它能反映目标的尺寸、强散射点位置、精细结构和材料质地等信息。HRRP相对于2维成像，不仅易于获得与处理，同时还避免了复杂的运动补偿运算，对目标识别具有重要意义[1－5]。

HRRP具有目标姿态敏感性，在一定的目标划分角域范围内，其回波幅值分布通常具有一定的统计特性[3－7]。HRRP帧内回波幅值统计模型主要分为两种，一种认为HRRP各距离分辨单元回波幅值分布具有近似独立性[8,9]，另一种则进一步考虑了HRRP各距离分辨单元回波幅值的相关统计特性[10,11]。由于HRRP各距离分辨单元回波幅值特征之间具有弱相关性，本文主要考虑第1种统计模型，即假设HRRP各距离分辨单元回波幅值分布近似独立。

文献[9]基于第1种统计模型，提出一种非参数化方法-基于累计量的随机学习算法(Stochastic Learning of the Cumulative,SLC)[12]来估计概率密度函数。在样本量充足时，该方法不仅可以准确地估计概率密度函数，而且不存在“窗宽”调节问题。然而，当训练样本量不足时，基于SLC的非参数化方法不能准确地进行概率密度估计，最终导致目标平均识别率下降。

文献[13]提出一种基于半参数化概率密度估计的雷达目标识别方法，通过有效利用雷达目标HRRP各距离分辨单元回波幅值分布的经验知识，并结合非参数化概率密度估计的优点来估计雷达目标HRRP各距离分辨单元回波幅值的概率密度，达到参数化方法和非参数化方法优缺互补的目的，提高雷达目标HRRP的识别率。

为了解决SLC非参数化概率密度估计方法在小样本条件下估计精度不高的问题，本文结合半参数化概念，提出一种基于半参数化SLC的雷达目标识别方法。该方法将通过SLC求解得到的非参数化概率密度估计表示为非参数化修正因子，再利用非参数化修正因子对Gamma分布假设条件下的参数化概率密度估计进行修正，提高小样本情况下SLC算法的雷达目标HRRP识别率。下文主要安排如下：第2节和第3节分别介绍SLC概率密度估计方法以及半参数化SLC概率密度估计；第4节利用5种飞机目标HRRP仿真数据对基于半参数化SLC的雷达目标识别方法进行分析和验证，并与其它基于统计建模的方法进行了比较；第5节给出结论。

2 SLC非参数化概率密度估计

已知1维随机变量x的N个相互独立的随机采样xn∈R,n=1,…,N,按升序排列，记为x1≤x2≤…≤xN。设x的分布函数 u=F(x)，则xn对应的分布函数值un=F(xn)(n=1,2,…,N)满足u1≤u2≤…≤uN。当N充分大时，可以证明 u n(n=1,2,…,N)应服从[0,1]上的均匀分布[12]。

将xn作为多层神经网络的输入，随机生成服从[0,1]上的均匀分布的N个点(n=1,2,…,N)，按升序排列，记为。比如，可取=n/ N(n=1,2,…,N)，将作为本次训练周期的期望输出。期望输出可以每次训练周期随机生成，为了提高收敛速度，也可以每隔L个周期随机生成一个期望输出。

调整神经网络权值 w(t+1)=w(t)+η(t)∂ ε(w)/∂ w，增加循环次数，直至目标函数ε(w)小于一个预先设定的阈值。其中，

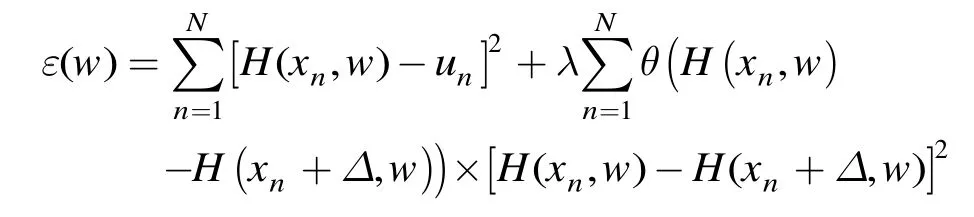
网络训练完毕，则输入测试样本x的网络输出H(w,x)即为其概率分布函数值。由于多层神经网络的激励函数一般都是任意阶可导函数，因此，概率密度函数 f(x)=H'(w,x)。采用SLC估计概率密度，在样本数充足的情况下，该算法不仅可以准确地估计密度函数，而且不存在传统的非参数化概率密度估计“窗宽”调节问题。但是随着样本数的减小，SLC算法表出概率密度函数的准确度下降。对于HRRP，根据散射中心模型，单个距离单元回波幅值分布主要分为3种情况[8]：第1种情况是距离分辨单元内没有明显的主散射中心，而只存在大量弱散射中心，其回波幅值服从瑞利分布；第2种情况是距离分辨单元内同时存在一个主散射中心和大量弱散射中心，其回波幅值服从莱斯分布；第3种情况是距离分辨单元内同时存在多个主散射中心(特别是包含2～3个主散射中心)

和大量弱散射中心，其回波幅值服从多峰分布，一般以双峰分布为主。特别当回波幅值呈多峰分布时，

SLC无法准确描述出多峰情况。图1给出了M2000

飞机模型在某方位角范围内两种典型的HRRP距离单元幅值分布直方图统计结果，实线表示SLC算法在样本数充足情况下表出的概率密度估计值，虚线表示SLC算法在样本数不足的情况下表出的概率密度估计值。由图1可以看出，特别是对于多峰分布的情况，SLC算法在小样本情况下表出的准确度大大降低。

3 半参数化 SLC概率密度估计及 HRRP识别

常用概率密度估计方法大致可以分为两类：一类是参数化概率密度估计，如高斯模型或 Gamma模型等，利用训练样本对概率密度模型的参数进行估计。参数化概率密度估计的优点是在样本数不足或者样本特征维数较高时，也可以较为准确地估计概率密度，其缺点是可能面临“模型失配”问题，影响识别效果。另一类为非参数化概率密度估计。非参数化方法可以估计任意形式的概率分布，但是需要大量的训练要本，计算复杂度也较高。

半参数化概率密度估计[13－15]较好地结合了上述两类方法的优点，它在数据分布具有一定先验知识的基础上，通过非参数化方法对参数化概率密度估计进行修正，达到提高概率密度估计精度的目的。

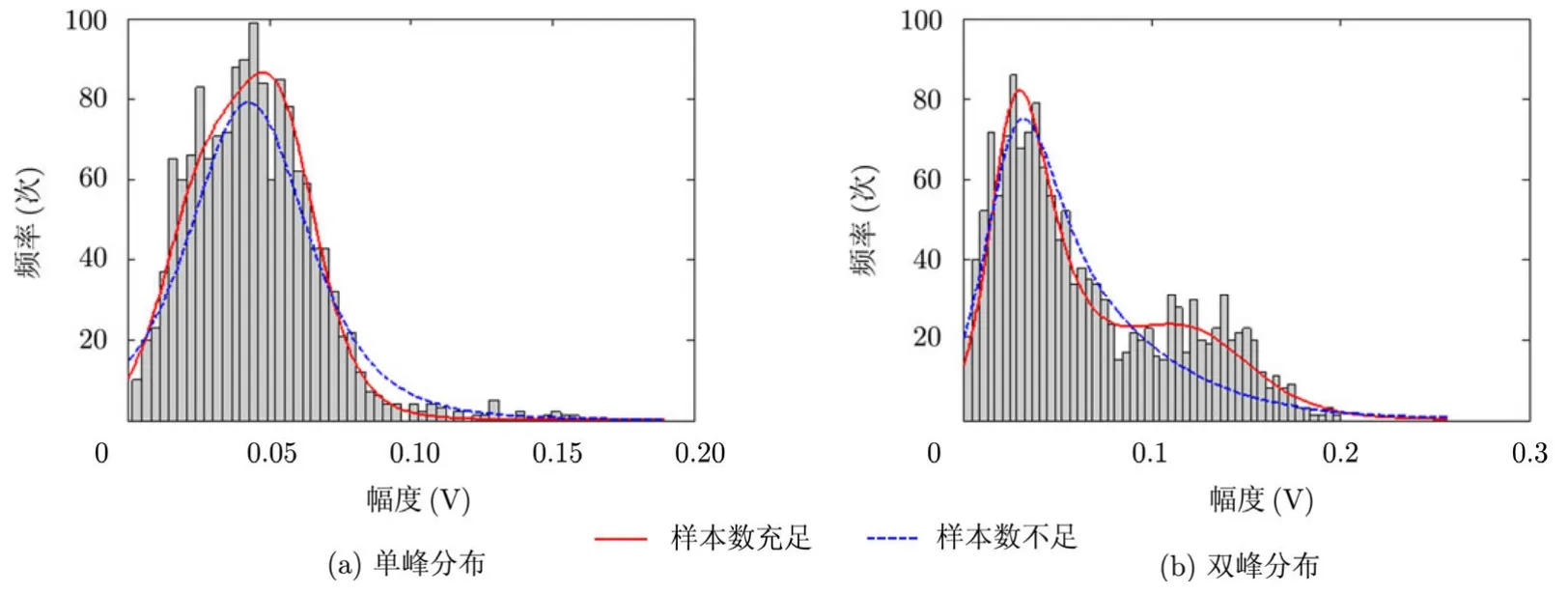
图1 SLC算法概率密度估计结果

为了提高在小样本情况下的平均识别率，结合半参数化概率密度估计概念，本文提出一种半参数化SLC概率密度估计方法，用于HRRP识别。该方法将通过 SLC求解得到的非参数化概率密度估计表示为非参数化修正因子，再利用非参数化修正因子对Gamma分布假设条件下的参数化概率密度估计进行修正，达到参数化方法和非参数化方法优缺互补的目的。最终提高在小样本情况下的目标识别率。

本文采用的非参数化修正因子的形式[14]为

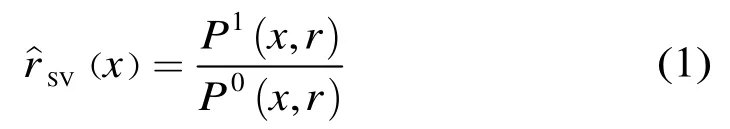
上式中，P(x,r)表示样本x处于以自身为球心，半径为r的球体B中的概率，即

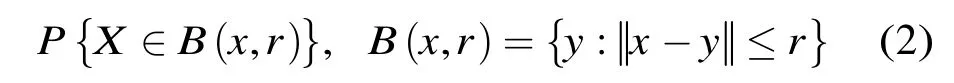
其中，P1为SLC算法对随机变量x的概率估计值，P0为参数化方法对随机变量x的概率估计值。因此，与式(1)对应的半参数化SLC概率密度估计函数可以表示为

在非参数化修正因子式(1)中，球半径r实际上充当了光滑因子的作用。当r增加时，非参数化修正因子曲线变得更加光滑。当球半径r趋近于0时，式(1)趋近于非参数化 SLC概率密度估计值和参数化概率密度估计值之比，此时，式(3)退化为非参数化SLC概率密度估计。而当球半径r增加到包含整个样本空间时，P0,P1以及式(1)刚好等于1，此时，式(3)又退化为参数化概率密度估计。因此，在实际使用半参数化SLC概率密度估计时，需要对球半径r进行设定，以满足最佳概率密度估计需求。

图2给出了M2000飞机模型在以0°俯仰角、60°方位角为中心的姿态下，15°角域划分内两种典型的HRRP距离分辨单元回波幅值分布的直方图、Gamma概率密度模型和半参数化SLC概率密度模型统计结果。由图 2可见，在回波幅值呈单峰分布的情况下，参数化方法和半参数化 SLC方法都能比较好地估计其概率密度；但在回波幅值呈双峰分布的情况下，参数化方法出现了“模型失配”问题，半参数化 SLC方法仍能比较准确地估计其分布情况。

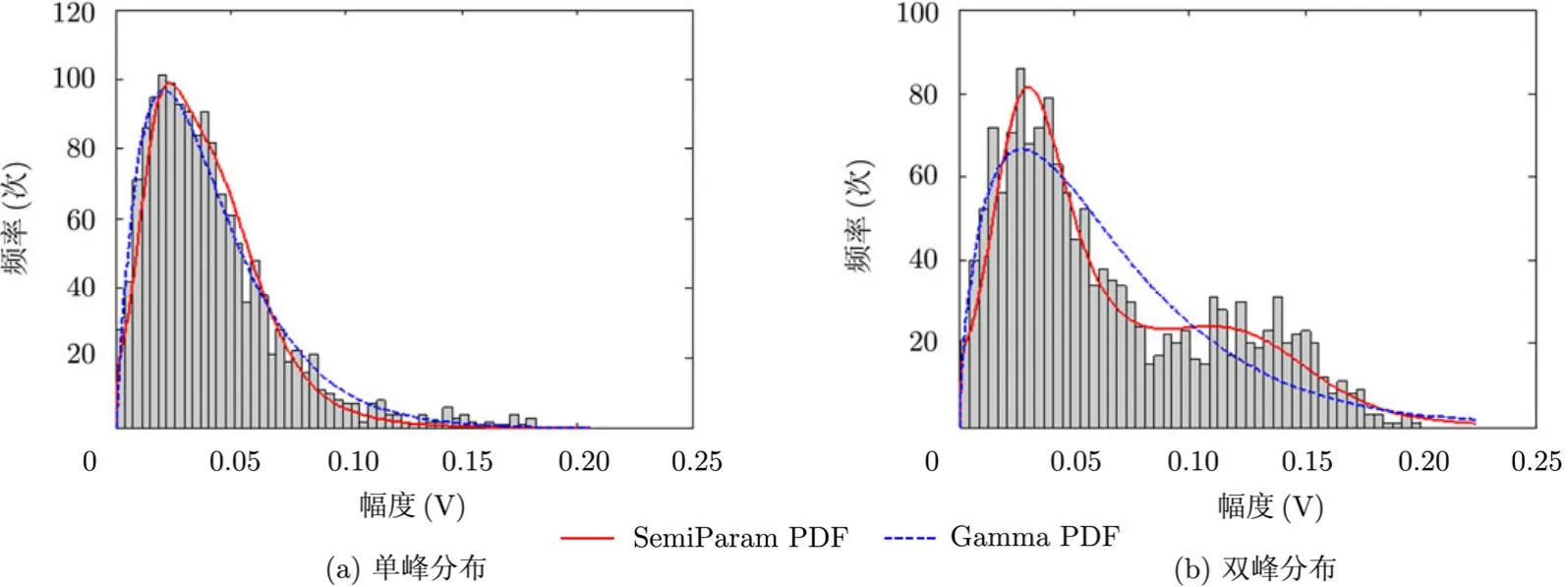
图2 M2000飞机模型HRRP参数化与半参数化SLC概率密度估计

本节最后对基于半参数化 SLC的雷达目标HRRP识别过程进行小结，该方法主要包括训练和测试两个阶段。

训练阶段：

(1) 将待识别目标的训练样本按角域分帧，各帧内的HRRP对齐并幅度归一化；

(2) 按式(3)统计每帧 HRRP 各距离分辨单元回波幅值的半参数化概率密度估计。由于雷达目标HRRP各距离分辨单元回波幅值分布具有近似独立性，因此，可以认为每帧HRRP的概率密度就是该帧HRRP各距离分辨单元回波幅值概率密度的乘积。

识别阶段：

(1) 假设各种飞机目标先验概率均相等，计算测试样本在每帧HRRP半参数化概率密度估计模型下的概率密度值；

(2) 根据贝叶斯决策规则把测试样本判别为最大概率密度值对应的目标。

4 实验与分析

4.1 实验数据及其预处理

实验选用南京航空航天大学目标特性研究中心提供的Su27,F16,M2000,J8II和J6等5种飞机全方位角转台仿真数据。雷达发射带宽500 MHz，并且在计算HRRP之前，分别对所有雷达I/Q两路通道数据添加高斯白噪声，主要分析信噪比为 20 dB条件下的HRRP数据。由于实验采用转台数据，因此不存在HRRP时移敏感性问题，针对幅度敏感性，所有HRRP均已实现2-范数归一化处理。

4.2 雷达目标HRRP识别结果及分析

实验主要比较分析了半参数化SLC算法应用于所选HRRP实验数据的识别性能，尤其在小样本情况下。在仿真实验中，SLC所对应的神经网络只有一个隐层，包含3个神经元。其中输入层到隐层的激励函数为tanh(x)，隐层到输出层的激励函数为logsig(x),η=0.0001,λ=1,Δ=0.001。

表1 是样本数充足时3种方法对5种飞机目标的详细识别结果。其中，参数化概率密度估计选用Gamma模型。由表1可见，当训练样本数充足时，非参数化SLC方法直接从训练数据本身出发，估计其分布情况，具有良好的灵活性，识别率优于参数化方法。半参数化SLC方法的平均识别效果介于参数化与非参数化SLC方法之间，而且在Su27和J6飞机目标的识别率上高于非参数化方法。

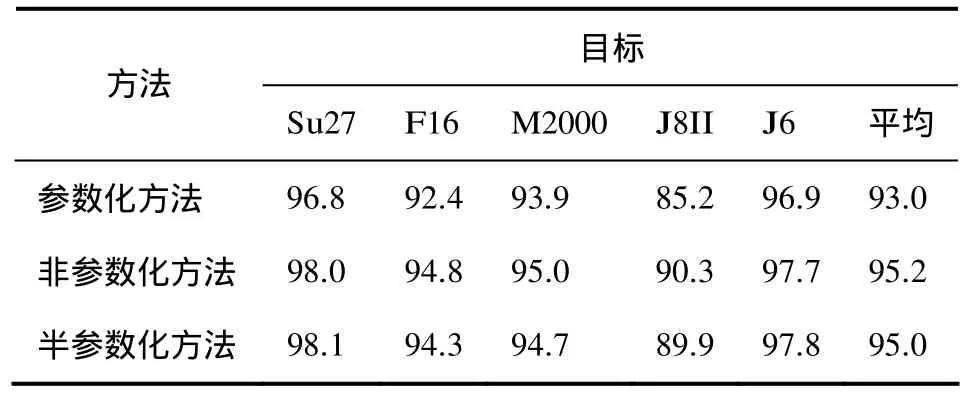
表1 信噪比为20 dB条件下训练样本数充足时3种方法的目标识别率(%)

但是当训练样本数减小，非参数化SLC方法的优势便逐渐下降，实验中分别选取训练样本数为60、55、50、45、40、35、30、25、20、15，图 3 是 3种方法的平均识别率随着样本量减少时的变化。由图3可以看到，在小样本情况下，非参数化SLC方法的平均识别率下降迅速，低于参数化方法。半参数化SLC方法有效利用了 HRRP 各距离单元幅值分布的经验知识，结合了参数化方法的优点，因而显示出良好的识别性能，在3种方法中平均识别率处于最高。

表2为训练样本数为25时，3种方法的详细识别效果。虽然从5种飞机目标个体的识别结果来看，半参数化SLC方法未必是最优的，但是就平均识别率来讲，半参数化SLC方法高于非参数化SLC方法。通过结合半参数化概念，提高了SLC算法在小样本雷达目标识别中的识别效果。在利用半参数化SLC概率密度估计时，面临最优光滑因子r的选择。图4为训练样本数为25时，半参数化SLC方法在不同的光滑因子作用下所取得的不同的平均识别率。由图4可以很清楚地看到，当光滑因子取值为1.2时，识别效果最好。当光滑因子大于1.2时，识别率迅速下降。

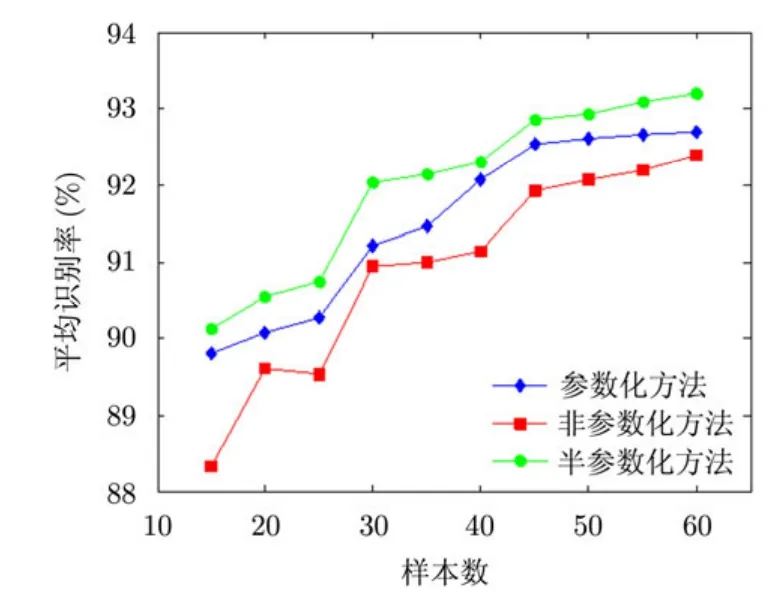
图3 小样本情况下3种方法随样本数变化的识别效果

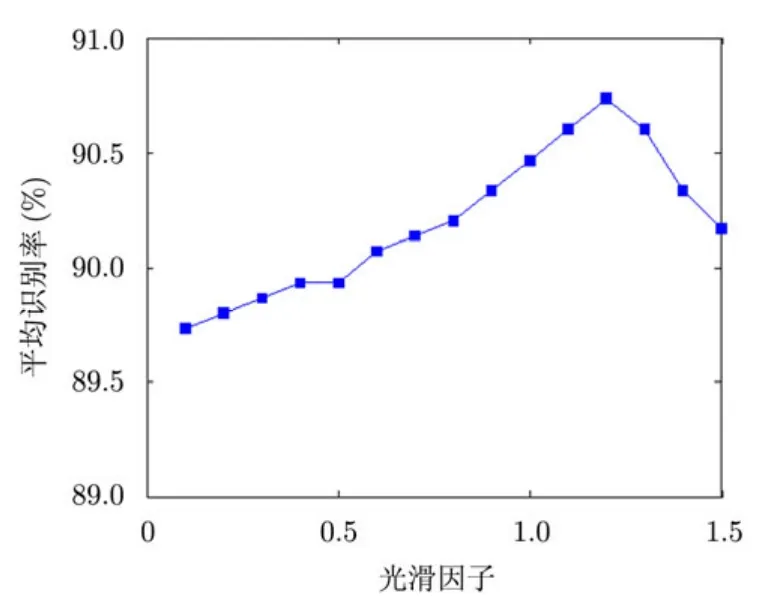
图4 半参数化SLC方法识别率随光滑因子的变化

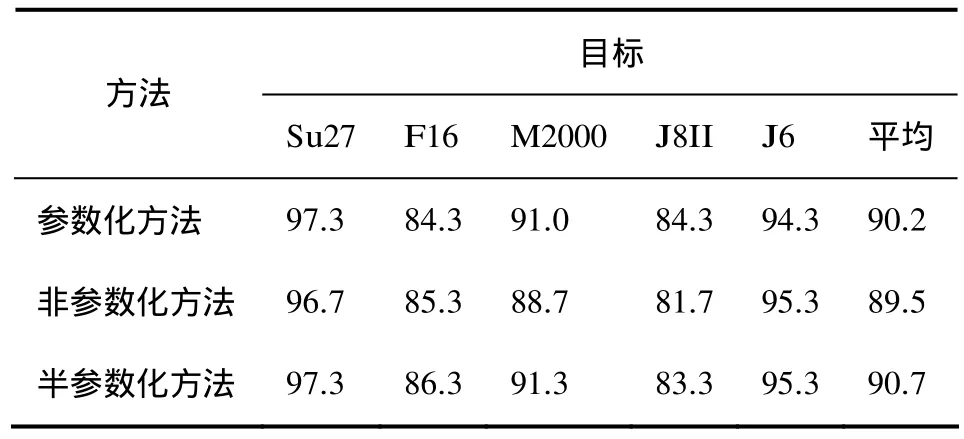
表2 信噪比为20 dB条件下训练样本数不足时3种方法的目标识别率(%)

5 结束语

非参数化SLC方法直接从训练数据本身出发估计其分布情况，不存在“窗宽”调节问题，具有良好的灵活性。但是在训练样本不充足的情况下，其概率密度估计的准确度大大降低，导致将其应用于雷达目标识别时识别率下降。为此，本文提出将SLC算法结合半参数化概念，通过SLC求解得到的非参数化修正因子对Gamma分布假设条件下的参数化概率密度估计进行修正，从而提高小样本情况下雷达目标的识别率。基于 5 种飞机目标 HRRP 的仿真实验表明，在小样本情况下，半参数化SLC概率密度估计下的雷达目标识别方法相比非参数化SLC方法具有更好的识别效果。

[1]王鹏辉,刘宏伟,杜兰,等.基于线性动态模型的雷达高分辨距离像小样本目标识别方法[J].电子与信息学报,2012,34(2):305-311.Wang Peng-hui,Liu Hong-wei,Du Lan,et al..Linear dynamic model based radar HRRP target recognition under small training set conditions[J].Journal of Electronics &Information Technology,2012,34(2): 305-311.

[2]Shi Lei,Wang Peng-hui,Liu Hong-wei,et al..Radar HRRP statistical recognition with local factor analysis by automatic Bayesian Ying-Yang harmony learning[J].IEEE Transactions on Signal Processing,2011,59(2): 610-617.

[3]Du L,Wang P,Liu H,et al..Bayesian spatiotemporal multitask learning for radar HRRP target recognition[J].IEEE Transactions on Signal Processing,2011,59(7):3182-3196.

[4]Zheng Tang-hong,Wang Yang,and Li Shi-guo.An HRRP preprocessing method and its application in radar targetrecognition[C].IEEE CIE International Conference on Radar,Chengdu,China,Oct.24-27,2011,1: 646-649.

[5]Wang P,Dai F,Pan M,et al..Radar HRRP target recognition in frequency domain based on autoregressive model[C].IEEE Radar Conference,Kansas City,USA,2011:714-717.

[6]Webb A R.Gamma mixture models for target recognition[J].Pattern Recognition,2000,33(12): 2045-2054.

[7]Copsey K and Webb A.Bayesian gamma mixture model approach to radar target recognition[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1201-1217.

[8]Du Lan,Liu Hong-wei,Bao Zheng,et al..A two-distribution compounded statistical model for radar HRRP target recognition[J].IEEE Transactions on Signal Processing,2006,54(6): 2226-2238.

[9]赵峰,张军英,刘敬,等.基于非参数化概率密度估计的雷达目标识别[J].电子与信息学报,2008,30(7): 1740-1743.Zhao Feng,Zhang Jun-ying,Liu Jing,et al..Radar target recognition based on nonparmetric density estimation[J].Journal of Electronics & Information Technology,2008,30(7):1740-1743.

[10]Du Lan,Liu Hong-wei,and Bao Zheng.Radar HRRP statistical recognition based on hypersphere model[J].Signal Processing,2008,88(5): 1176-1190.

[11]Du Lan,Liu Hong-wei,and Bao Zheng.Radar HRRP statistical recognition: parametric model and model selection[J].IEEE Transactions on Signal Processing,2008,56(5): 1931-1944.

[12]Malik Magdon-Ismail and Amir Atiya.Density estimation and random variate generation using multilayer networks[J].IEEE Transactions on Neural Networks,2002,13(3):497-520.

[13]朱劼昊,周建江,吴杰,等.基于半参数化概率密度估计的雷达目标识别[J].电子与信息学报,2010,32(9): 2161-2166.Zhu Jie-hao,Zhou Jian-jiang,Wu Jie,et al..Radar target recognition based on semi-parametric density-estimation[J].Journal of Electronics & Information Technology,2010,32(9):2161-2166.

[14]Chaudhuri P,Ghosh A K,and Oja H.Classification based on hybridization of parametric and nonparametric classifiers[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(7): 1153-1164.

[15]Hjort N L and Glad I K.Nonparametric density estimation with a parametric start[J].Annals of Statistics,1995,23(3):882-904.