基于自适应阈值选择的非参量GS检测算法

张 林 赵志坚 关 键 何 友

(海军航空工程学院电子信息工程系 烟台 264001)

1 引言

在参量CFAR(Constant False Alarm Rate)检测技术中，人们为了解决CA(Cell Averaging)[1]检测算法在杂波边缘中引起虚警概率上升和在多目标环境中导致检测性能下降的问题分别提出了GO(Greatest Of)[2]检测算法和 SO(Smallest Of)[3]检测算法，最近由Smith和Varshney提出了基于自适应阈值选择VI(Variability Index)[4－8]检测算法，该检测算法通过均值比 MR(Mean Ratio)和可变性指标VI假设检验，实现CA,GO和SO检测算法之间的转换，它在均匀和非均匀背景下都具有较强的自适应性。

在雷达目标检测理论中，非参量检测算法因其不依赖于背景杂波的具体分布形式而比参量检测算法具有更强的环境适应能力。传统非参量检测算法如 GS(Generalized Sign)[9－14]检测算法是通过检测单元与参考单元的比较构造相应的检验统计量。采用这种方式得到的非参量检测算法通常要求检测单元两侧杂波背景均匀，但是，当目标位于多目标环境中时，由于杂波背景均匀的条件难以保证，GS检测算法的检测性能下降。

近些年来为了提高 GS检测算法在非均匀环境中的检测性能分别提出了 GO-GS(Greatest Of Generalized Sign)检测算法和TGS(Trimmed Generalized Sign)[15]检测算法。本文将VI检测算法的设计思想引入GS检测算法的设计中，提出VI-GS检测算法。其中，VI-GS检测算法是利用VI和MR假设检验，实现GS,TGS和GO-GS检测算法之间的转换，从而提高 GS检测算法在多目标环境的检测性能。

本文利用仿真数据和实测海杂波数据分析了上述VI-GS检测算法的检测性能，并与GS检测算法进行对比，结果表明，VI-GS检测算法适用于海杂波中目标检测问题。

2 典型的非参量检测算法模型

2.1 GS检测算法模型

GS检测算法的检验统计量由下式来描述

式中，N表示脉冲数，M表示参考单元数；yj表示检测单元采样值，xji表示参考单元采样值，GS检测算法是将临近N个脉冲的秩值rj进行相加形成检验统计量TGS。

2.2 TGS和GO-GS检测算法模型

2.1 节给出了GS检测算法第j次扫描的检测策略，下面以式(2)中的观测样本为检验统计量的基础，给出TGS检测算法和GO-GS检测算法的的检测策略

TGS检测算法是将邻近N个脉冲中秩值大于参考单元数一半的秩值进行相加形成检验统计量，并与门限相比较形成目标有无的判断；GO-GS检测算法选取局部估计中较大者求和作为全局估计检验统计量，并与门限相比较形成目标有无的判断。

3 VI-GS设计思想及理论依据

基于自适应阈值选择的非参量GS检测算法是通过均值比MR假设检验和可变性指标VI假设检验的结果对杂波背景进行估计，其中2阶统计量VI的定义如式(7)所示：

式中，Xi代表第i个参考单元的采样值，M代表参考单元数，为样本方差，为样本均值。通过VI和门限KVI相比较，作出前(后)参考单元是否均匀的判断，假设检验式为

均值比统计量MR的定义如下：

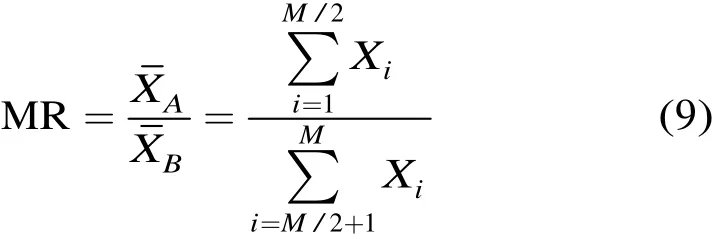
表1为VI-GS检测算法的自适应逻辑选择，其中，通过VI和MR假设检验即可得到相应的杂波背景。表中第1行对应着均匀杂波背景，用GS检测算法即能得到较好的检测性能；表中第2行对应着杂波边缘背景，此时采用GO-GS检测算法有较好的虚警控制能力；表中第3(4)行对应着前(后)沿滑窗存在干扰目标的情况，此时采用半滑窗的GS检测算法有较好的检测性能，该检测算法利用检测单元与前(后)沿滑窗中均匀一侧的参考单元进行比较形成检验统计量，可很好地对抗干扰目标出现在单侧滑窗的情况；表中第5行主要对应着多目标环境，此时采用TGS检测算法有较好的检测能力。

表1 VI-GS的自适应选择

4 基于仿真数据分析

第3节介绍了VI-GS检测算法的工作原理，本部分主要利用Monte Carlo仿真的方式分析了VI-GS检测算法在两侧参考单元中存在多目标干扰的情况下对主目标的检测性能，并与GS检测算法的性能进行比较。其中脉冲数为10，参考单元数为16，虚警概率为 10−4，干扰目标与主目标的信杂比比值为1，干扰目标和主目标的仿真均采用Swerling Ⅱ型目标，杂波为高斯分布杂波，其中Monte Carlo次数为105。

4.1 单一主目标情况

首先比较单一主目标情况下的VI-GS检测算法与GS检测算法的检测性能差异，图1给出了两检测算法的信杂比与检测概率对应关系曲线。纵坐标表示检测概率的变化范围从0到1，横坐标表示信杂比的变化范围从−5 dB到15 dB。

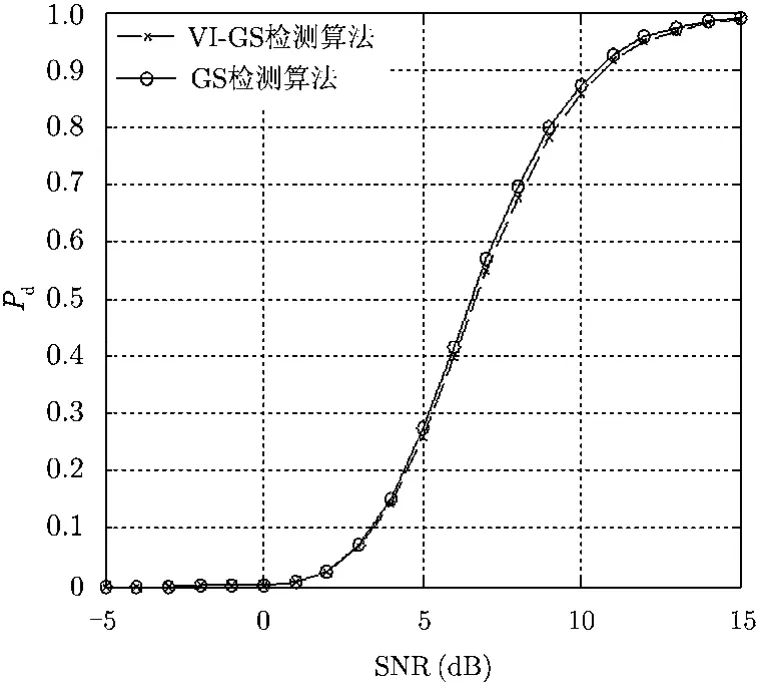
图1 单一主目标情况

由图1可以看出，第一，在信杂比的变化范围内两种检测算法对Swerling Ⅱ型目标的检测性能接近，其中GS检测算法略高于VI-GS检测算法，这主要是因为在单一主目标环境下，VI-GS检测算法选择逻辑对应全滑窗的 GS检测算法，因此两种检测算法性能接近，但是由于周围杂波是起伏的，在进行逻辑选择时，将会引入其它选择的结果，此时检测结果有一定的下降，但是幅度不大；第二，一般认为信杂比小于6 dB的目标为微弱目标，当信杂比为6 dB时，GS检测算法对应的检测概率为0.4157,VI-GS检测算法对应的检测概率为0.3981，均未超过0.5，此时可以通过增大脉冲数来提高两种检测算法的检测性能。

4.2 单一干扰目标情况

图2 单一干扰目标情况

图2给出了参考单元内存在单一干扰目标时VI-GS检测算法和GS检测算法的信杂比与检测概率对应关系曲线。纵坐标表示检测概率的变化范围从0到1，横坐标表示信杂比的变化范围从−5 dB到15 dB。

由图2中两条曲线的相对关系可以看出，第一，对3 dB到15 dB之间的目标进行检测时VI-GS检测算法的检测性能要明显优于GS检测算法，在信杂比为6 dB处VI-GS检测算法比GS检测算法的检测性能高出约5.84%，随着信杂比的增大，差距进一步增大，当信杂比达到10 dB时，VI-GS检测算法比GS检测算法的检测概率高出7.65%，分别达到0.72和0.64的检测概率，另外，在0.5的检测概率条件下GS检测算法比VI-GS检测算法的检测性能损失约为0.71 dB，这主要是因为干扰目标为1时，VI-GS检测算法选择逻辑对应单滑窗的GS检测算法，即选择前(后)滑窗中为均匀的滑窗进行计算，此时干扰目标所在的参考滑窗由于不均匀而不被选择，故干扰目标对VI-GS检测算法的影响减小，而GS检测算法由于采用全滑窗的方式，在计算检验统计量时不可避免地引入了干扰目标，因此其检测性能不如VI-GS检测算法；第二，当信杂比小于3 dB时，两种检测算法检测性能趋于一致，主要是因为当信杂比小于3 dB时，目标相比于周围杂波的优势已经很弱，在与周围参考单元进行比较时出现较多0值，目标难以被检测，此时，可以通过增大脉冲数来改善其检测性能，另外，对于单侧滑窗存在干扰目标的情况，由于VI-GS检测算法的逻辑选择对应于单侧滑窗GS检测算法，单侧干扰目标的个数对其影响不大，而GS检测算法的检测性能将会随着干扰目标数的增多而不断下降，因此对于单侧滑窗存在干扰目标的情况，VI-GS检测算法的检测性能高于GS检测算法。

4.3 2个干扰目标情况

图3给出了参考单元内存在2个干扰目标时VI-GS检测算法和GS检测算法的信杂比与检测概率对应关系曲线，由前面的分析可以知道，当2个干扰目标位于同侧时，VI-GS检测算法的检测性能高于GS检测算法，因此此时分析的为2个干扰目标位于检测单元两侧的情况，纵坐标表示检测概率的变化范围从0到1，横坐标表示信杂比的变化范围从−5 dB到15 dB。

图3 2个干扰目标情况

由图3可以看出，第一，对3 dB到15 dB之间的目标进行检测时VI-GS检测算法的检测性能明显优于GS检测算法，在信杂比6 dB处VI-GS检测算法比GS检测算法检测概率高出约4.81%，另外，在0.5的检测概率条件下GS检测算法比VI-GS检测算法的检测性能损失约为0.62 dB，这主要是因为2个干扰目标位于检测单元两侧，VI-GS检测算法选择逻辑对应TGS检测算法，而TGS检测算法在干扰目标为2时有优于GS检测算法的检测性能，故VI-GS检测算法的检测性能优于GS检测算法；第二，相比于单一干扰目标情况，干扰目标为2时，两种检测算法检测性能均有一定的下降，其中当信杂比为 6 dB时，GS检测算法检测性能下降为7.65%，VI-GS检测算法检测性能下降为8.55%。

4.4 3个干扰目标情况

图4给出了参考单元内存在3个干扰目标时VI-GS检测算法和GS检测算法的信杂比与检测概率对应关系曲线，由前面的分析可以知道当3个干扰目标位于同侧时，VI-GS检测算法的检测性能高于GS检测算法，因此此时分析的为2个干扰目标位于检测单元一侧，另一个目标位于检测单元另一侧的情况，其中横纵坐标表示含义与前面一致。从图中可以看出，VI-GS检测算法的性能明显优于GS检测算法，信杂比为6 dB时，比GS检测算法的检测概率高5.03%，随着信杂比的增大，检测性能差距不断增大，当信杂比为10 dB时，VI-GS检测算法的检测概率比GS检测算法的检测概率高13.4%，当信杂比为15 dB时，VI-GS检测算法的检测概率比GS检测算法的检测概率高14.9%，相比于干扰目标数为0,1和2的情况，两种检测算法的检测性能进一步下降，在信杂比区间内，两种检测算法的检测概率均未超过0.8。

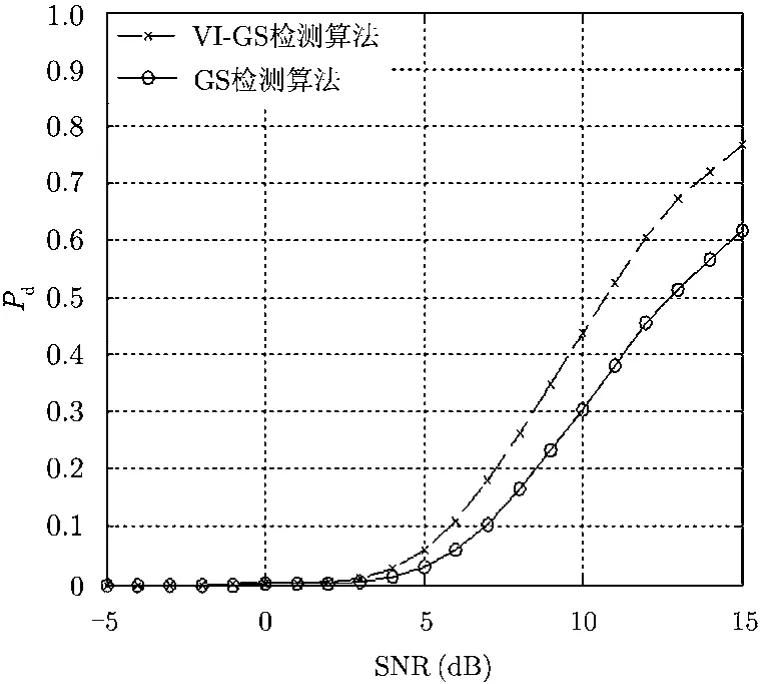
图4 3个干扰目标情况

4.5 4个干扰目标情况

图5是VI-GS检测算法和GS检测算法在4个干扰目标情况下对主目标的检测性能曲线图，纵坐标表示检测概率的变化范围从0到1，横坐标表示信杂比的变化范围从−5 dB到15 dB。此处分析的是检测单元前(后)两侧滑窗各存在2个干扰目标的情况。从图中可以看出，VI-GS检测算法的检测性能明显优于GS检测算法，当信杂比为5 dB和15 dB之间，两种检测算法的检测性能差距不断增大，当信杂比为15 dB时，VI-GS检测算法的检测概率比GS检测算法的检测概率高32.2%，相比于干扰目标数为0,1,2和3的情况，两种检测算法的检测性能进一步下降，另外对于整个信杂比区间，GS检测算法的检测概率较低，均未超过0.35。

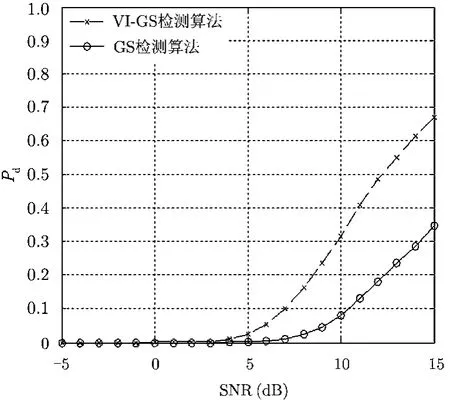
图5 4个干扰目标情况

5 基于雷达实测数据分析

第4节利用仿真数据对GS检测算法和VI-GS检测算法进行了分析，分析表明VI-GS检测算法除了在单一主目标情况下有近似于 GS检测算法的性能，在多目标环境均有优于 GS检测算法的检测性能。另外，随着干扰目标数的增大，VI-GS检测算法的性能优势更为明显。本小节主要利用某型雷达实测数据对VI-GS检测算法在多目标环境的检测性能进行分析，并与GS检测算法进行对比。其中图6给出了雷达原始视频数据的回放结果，该批数据可以用来分析不同非参量检测算法在多目标环境中的目标检测性能。

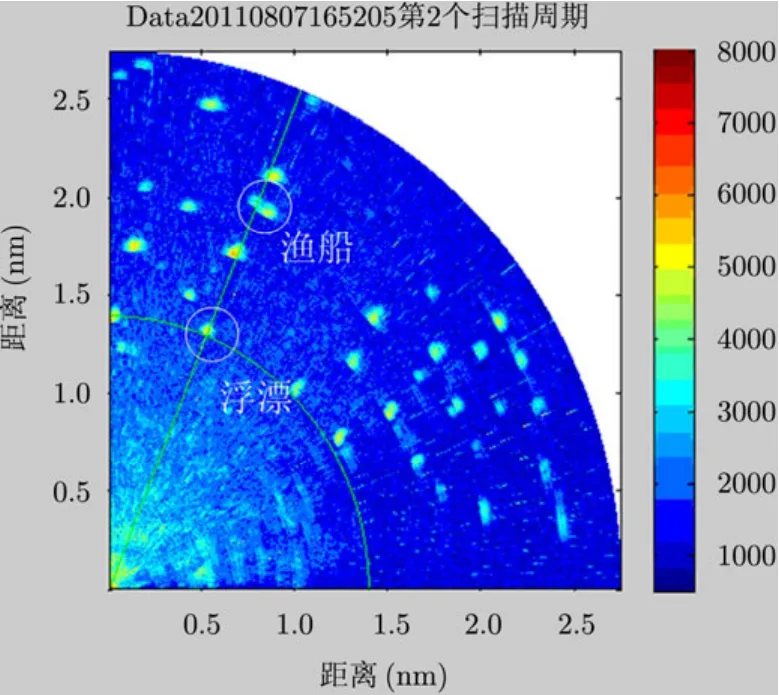
图6 雷达原始视频数据回放结果

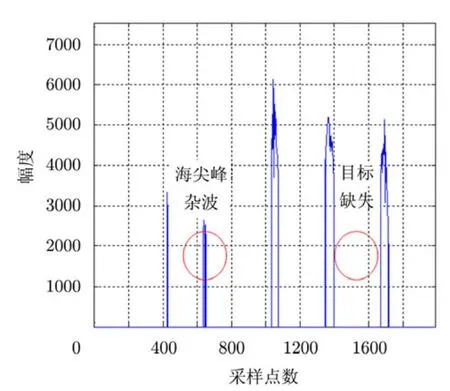
图7 GS检测算法处理结果

图8 VI-GS检测算法处理结果

图7和图8分别给出了22°方位(图6中绿色直线标注处)GS检测算法和VI-GS检测算法处理后幅度采样点图，其中虚警概率为 10−6，脉冲数为10，参考单元数为32。从图7和图8可以看出，VI-GS检测算法检测出了GS检测算法缺失的目标，这主要是因为该批目标的信杂比小于其它3批干扰目标，在进行GS检测算法处理时，对于图中标注的目标，由于较强目标进入到了参考单元内导致目标相比于周围参考单元的优势下降，从而影响检测，而对于VI-GS检测算法，此时逻辑选择对应于TGS检测算法，该检测算法在多目标环境中有更优的检测性能，因此图中标注的目标能够被检测，这也与前面的仿真分析相一致。另外，VI-GS检测算法抑制了GS检测算法未去除的一处海尖峰杂波(图7中圆圈处标注)。

6 结束语

本文主要研究了海杂波中非均匀杂波背景下的非参量GS检测算法，提出了一类新型的非参量GS检测算法，即自适应阈值选择的非参量GS检测算法(VI-GS)，并利用仿真数据和实测数据对该检测算法进行分析，研究表明：本文提出的VI-GS检测算法在多目标环境中相比GS检测算法有更好的检测性能，并且随着干扰目标数目的增多，检测性能优势更加明显，在单一主目标情况下，VI-GS检测算法的检测性能与GS检测算法相接近。另外，这种新型检测算法在log-normal分布、Weibull分布和杂波边缘的检测性能有待于进一步研究。

[1]Finn H M and Johnson R S.Adaptive detection mode with threshold control as a function of spatially sampled clutterlevel estimates[J].Radio Corporation of America Review,1968,29(9): 414–464.

[2]Hansen V G.Constant false alarm rate processing in search radars[C].IEEE International Radar Conference,London,1973: 325–332.

[3]Trunk G V.Range resolution of targets using automatic detectors[J].IEEE Transactions on Aerospace & Electronic Systems,1978,14(5): 750–755.

[4]Smith M E and Varshney P K.Intelligent CFAR processor based on data variability[J].IEEE Transactions on Aerospace& Electronic Systems,2000,36(3): 837–847.

[5]郝程鹏,侯朝焕,王维建.基于改进的VI-CFAR算法的分布式CFAR检测[J].系统仿真学报,2007,19(4): 830–832,908.Hao Cheng-peng,Hou Chao-huan,and Wang Wei-jian.Distributed CFAR detection based on modified VI-CFAR algorithm[J].Journal of System Simulation,2007,19(4): 830–832,908.

[6]徐从安,简涛,何友,等.一种改进的VI-CFAR检测器[J].信号处理,2011,27(6): 926–931.Xu Cong-an,Jian Tao,and He You,et al..An improved VI-CFAR detector[J].Signal Processing,2011,27(6): 926–931.

[7]范时胜,王立振.一种改进的VICFAR检测器[J].空军雷达学院学报,2010,24(5): 313–315.Fan Shi-sheng and Wang Li-zhen.A sort of improved VICFAR detector[J].Journal of Air Force Radar Academy,2010,24(5): 313–315.

[8]Smith M E and Varshney P K.VI-CFAR: a novel CFAR algorithm based on data variability[C].IEEE International Radar Conference,Edinburgh,UK,1997: 263–268.

[9]何友,关键,彭应宁,等.雷达自动检测与恒虚警处理[M].北京: 清华大学出版社,1999: 230–257.He You,Guan Jian,Peng Ying-ning,et al..Automatic Radar Detection and CFAR Processing[M].Beijing: Tsinghua University Press,1999: 230–257.

[10]Hansen V G and Olsen B A.Nonparametric radar extraction using a generalized sign test[J].IEEE Transactions on Aerospace & Electronic Systems,1971,7(5): 942–950.

[11]孟祥伟.韦布尔杂波下非参数量化秩检测器的性能[J].电子学报,2009,37(9): 2030–2034.Meng Xiang-wei.Performance of rank quantization(RQ)nonparametric detector in Weibull background[J].Chinese Journal of Electronics,2009,37(9): 2030–2034.

[12]金伟,刘向阳,许稼.K分布雷达杂波中两种非参量检测器性能分析[J].雷达科学与技术,2010,8(4): 357–361.Jin Wei,Liu Xiang-yang,and Xu Jia.Performance analysis of two nonparametric detectors in K-distributed clutter[J].Radar Science & Technology,2010,8(4): 357–361.

[13]赵志坚,关键.海杂波中非参量恒虚警检测器性能分析[J].雷达科学与技术,2010,8(1): 65–68.Zhao Zhi-jian and Guan Jian.Performance analysis of nonparametric CFAR detectors in sea clutter[J].Radar Science & Technology,2010,8(1): 65–68.

[14]Sanz-Gonzalez J L and Alvarez-Vaquero F.Nonparametric rank detectors under K-distributed clutter in radar applications[J].IEEE Transactions on Aerospace &Electronic Systems,2005,41(2): 702–710.

[15]Al-Hussaini E K.Trimmed generalized sign and modified median detector for multiple target situations[J].IEEE Transactions on Aerospace & Electronic Systems,1979,15(4): 573–575.