MATLAB模拟动力系统吸引子

冯泽夫，段秀庆，杨 航，艾文会

（华中师范大学 数学与统计学院，湖北 武汉 430079）

1 引言

MATLAB是由美国mathworks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境.它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言（如C、Fortran）的编辑模式，代表了当今国际科学计算软件的先进水平.利用MATLAB仿真模拟可以解决生产生活中很多问题，以前的蒙特卡洛方法结合计算机仿真模拟技术后不仅可以避免实验带来的损失可以得到非常理想的实验结果，如灯泡的寿命的测定，战争的模拟……，如果真正去实验会带来不少的损失，而用MATLAB仿真模拟，只需要我们输入约束条件和初始值，可以做多次试验得到较为理想的结果.本文正是这方面应用的体现，对吸引子设计数学模型，利用MATLAB求解洛伦兹方程数值解并绘制吸引子形成的动画，可以让读者真正理解吸引子形成的过程，并且在求解过程中我们发现初值不同得到的结果可能有很大变化，从而发现动力系统吸引子的混沌现象.

2 动力系统吸引子的概念及数值模拟的重要意义

动力系统在高维相空间中所描述出来的相对低维的稳定轨道被称为吸引子.简言之，吸引子是指这样的一个集合，当时间趋于无穷大时，在任何一个有界集上出发的非定常流的所有轨道都趋于它.相空间中满足以下3个条件的点的集合(可能包含1个点、有限个点或无限个点)，被称为动力学系统的吸引子.

2.1 终极性

处于非目的态的系统“不安于现状”，力求离之远去，处于目的态的系统则“安于现状”，自身不再愿意或无力改变这种状态（也可以叫做惰性）.

2.2 稳定性

目的态是系统自身质的规定性的体现，这种规定性只有在稳定状态中才能确立起来并得到保持，不稳定状态不可能成为目的态；

2.3 吸引性

吸引性是目的性的根本要素，没有吸引力的状态不能成为系统演化所追求的目标.

吸引子是刻画系统整体特性的概念，具有不可分割性，即不能把它划分为两个都满足定义要求的 较小集合.也不能把几个吸引子组合为一个吸引子，如平衡态A与周期态B不能合成一个单一的吸引子.吸引子分为平庸吸引子和奇异吸引子，对于平庸吸引子来说，无论初值如何，终值只有一个，而奇异吸引子却有无数个终值，即奇异吸引子是无数个点的集合，对初值极端敏感.通过对时间序列的相空间重构，构造的奇异吸引子可在一定程度上反映出系统的演化规律，而通过分析相空间重构吸引子的结构，就可以进一步评价动力学系统的混沌特性及其变化.

而奇异吸引子可以用matlab模拟仿真它的产生，现在该方法广泛应用于流体力学，气象学灾害预报预报，地震预测及信号处理等领域.特别的，在计算机上用洛伦兹所建立的微分方程模拟气候变化，可以发现初始条件的极细微差别可以引起模拟结果的巨大变化—轨线的行为无法预测，这表明天气过程以及描述它们的非线性方程是如此的不稳定，这正如众所周知的天气的“蝴蝶效应”即：南美洲亚马逊河流域热带雨林的一只蝴蝶偶然拍动一下翅膀，几星期后可以在美国德克萨斯州引起一场龙卷风.从而气象学家应用此法进行天气预报的研究.

3 模拟方案

3.1 模拟的基本思路

3.1.1 模型准备：了解问题的实际背景，明确建模目的，搜集必要的信息如现象、数据等，尽量弄清对象的主要特征，形成一个比较清晰的“问题”，由此初步确定用哪一类模型.

3.1.2 模型假设 根据对象的特征和建模的目的，抓住问题的本质，忽略次要因素作出必要的、合理的简化假设.

3.1.3 模型构成 根据所作的假设，用数学的语言、符号描述对象的内在规律，建立包含常量、变量等的数学模型，如优化模型、微分方程模型、差分方程模型、图的模型等.

3.1.4 模型求解 可以采用解方程、画图形、优化方法、数值计算、统计分析、模型对数据的灵敏性分析、对假设的强健性分析.

3.2 模拟洛伦兹吸引子

lorenz方程描述了从水桶底部加热时，桶内液体运动的情况.加热时，底部的液体温度上升并产生对流现象，当提供足够的热量并保持不变时对流就产生不规则的运动和湍流，形成混沌系统.

3.2.1 建立模型：下面的洛伦兹微分方程组的求解过程演示了吸引子的形成过程.

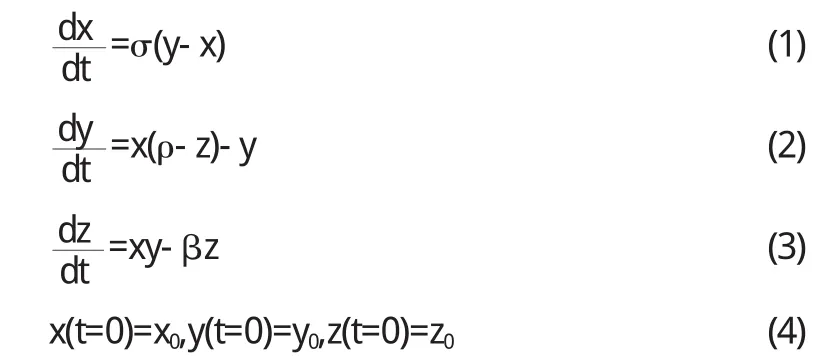
其中x正比于液体对流运动翻动的速率，y正比于液体上流与下流的温差的变化，z正比于竖直方向的温度梯度，式中三个参数σ（Prandtl数）、β和ρ（Rayleigh数）可任取大于0的数值，其中ρ是该动力系统中重要的参数.当系数σ、ρ、β在一定范围内取值时，三个变量x,y,z在相空间构造的吸引子呈现出相似的结构特征.一般常用的组合是σ=10，β=，让ρ取不同的数值，分析吸引子图像.

3.2.2 方程的离散化:可以采用欧拉法或4阶龙格-库塔法迭代法对微分方程组求数值解.

3.2.3 洛伦兹方程求解

本文说明用Matlab工具箱求解洛伦兹方程的过程，并给出吸引子的三维动态图象.洛伦兹方程如下：

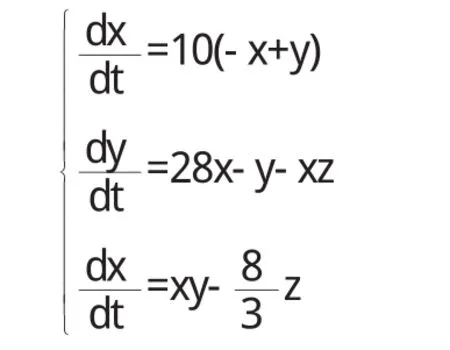
这是一个自洽的方程组，用matlab2010求解结果如下：如图1.

3.2.4 动态显示吸引子并生成动画程序略，验证蝴蝶效应得到结果如图2.

4 讨论及结论

4.1 在ρ取不同的值时我们发现如下规律：ρ较小时如0.9，该lorenz动力系统是稳定的，吸引子最终演化到两个奇点中的一个，而随着ρ的值增大，系统变得越来越复杂，轨线的变化越来越难以预测，特别的当ρ取28时出现了混沌现象.

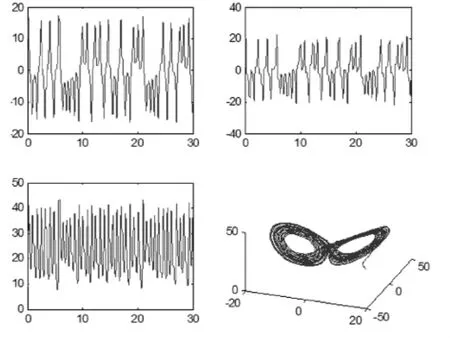
图1

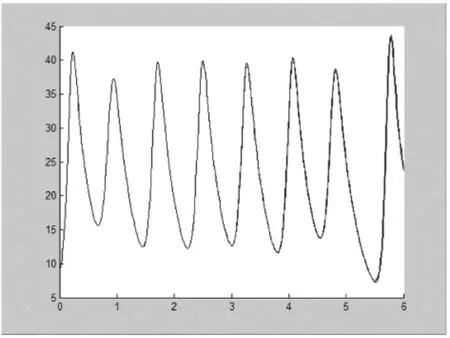
图2

4.2 洛伦兹动力系统本身有确定的动力学方程（式（1）、（2）和（3）），该动力学方程的初值、参数值的选取直接关系到该方程是否出现混沌状态.

4.3 吸引子之外的所有轨线最终将归宿到吸引子范围之内，体现出耗散系统的终态最终都将收缩到吸引子上，平庸吸引子的终值只有一个，而奇异吸引子本身由既折叠又分离的轨线构成，并且无法确定其未来的轨线的发展趋势，这表明混沌系统是一种整体收敛而局部发散的动力学系统.

4.4 利用MATLAB语言进行计算机数值仿真模拟，求解微分方程数值解，操作简单，图形逼真.通过仿真实验，读者对混沌系统的特性和细节会有直观深刻的理解.计算机matlab对于混沌的研究正发挥着无可替代的作用.

〔1〕姜启源，谢金星，等.数学模型（第四版）[M].北京：高等教育出版社，2010.

〔2〕陆安山.混沌系统的仿真实现[J].钦州师范高等专科学校学报，2006（6）.

〔3〕陈永胜.基于MATLAB求解Rossler方程和模拟仿真[J].牡丹江师范学院学报，2009（1）.