一种改进的Fitz载波频偏估计方法及其仿真

孟庆萍,周新力,田 伟

(1.海军航空工程学院 研究生管理大队,山东烟台 264001;2.海军航空工程学院 电子工程系,山东烟台 264001;3.海军航空工程学院 训练部,山东 烟台 264001)

1 引 言

在无线通信系统中,收发双方的载波频率偏移严重影响了系统性能。关于载波频偏估计的方法很多文献进行了探讨[1-13]。就目前的载波频偏估计方法来看,其频偏捕获范围、估计精度以及抗噪声性能之间存在矛盾。当接收端信噪比低于某信噪比门限时,估计性能会迅速恶化,无法满足接收机解调的要求。因此,研究低信噪比条件下的大频偏估计问题具有十分重要的意义。

目前频偏估计方法主要分为两类:基于时域的估计方法和基于频域的估计方法[14]。基于时域估计方法的频率估计器硬件消耗相对较小,它有几种不同的实现结构,可以归结为两种形式:基于相邻接收信号差分和基于自相关函数的方法。其中基于相邻接收信号差分的频偏估计方法捕获范围大,但估计精度低;基于自相关函数的频偏估计方法由于利用自相关函数的相位估计频偏,所以其估计精度高,但是其捕获范围小。本文给出一种基于自相关函数的改进Fitz算法,它利用自相关函数序列的差分代替自相关函数的相位估计载波频偏,解决了其捕获范围小的问题,并且保持了其较低的信噪比门限,可以实现大频偏和低信噪比条件下的高精度估计。

2 经典频偏估计方法及比较

假设发送信号的调制方式为MPSK,接收信号经过系统均衡,不存在符号同步误差,均衡后的信号近似符合加性高斯白噪声条件,码间干扰可以忽略,则均衡输出的信号可以表示为

式中,sk为调制后的发送数据,Δf为信号载波频偏,n(k)为独立同分布的零均值复噪声信号,噪声方差为σ2。对于接收信号 x(k),采用数据辅助的频偏估计方法,将已知数据 sk取共轭后与接收信号相乘,可以得到:

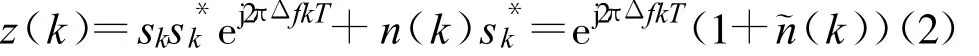
式中,＊表示取共轭运算。

时域频偏估计方法分为两类,一类利用接收信号的差分信息估计频偏,称为基于接收信号差分的频率估计方法。此类方法以L&W方法[1]和Kay[2]方法为代表。

L&W方法:

Kay方法:

式中,w1和w2为用于平滑的窗函数。

基于接收信号差分的频偏估计方法估计范围大,理想情况下可以估计的归一化频偏(ΔfT)范围为(-0.5,0.5),并且都是无偏估计;但是这类估计方法的信噪比门限非常高,也就是说仅在非常大的信噪比条件下才能达到CRB界(Cramer-Rao),信噪比门限以下的估计性能迅速恶化。

由于没有充分利用信号的统计特性,基于相邻接收信号差分的频偏估计方法抗噪声性能很差。另一类基于自相关函数的频偏估计方法充分利用了信号的统计特性,使得其抗噪声性能增强,信噪比门限大大降低。这类方法以Fitz[3]、L&R[4],以及M&M[5]方法为代表。设:

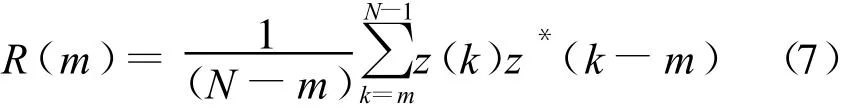
Fitz方法:

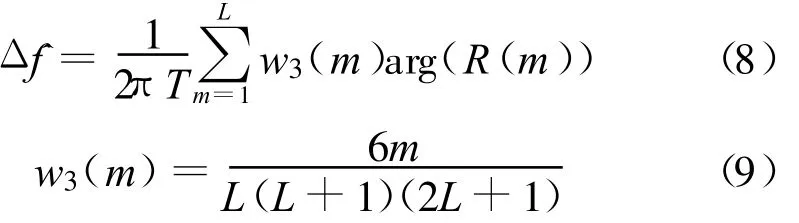
L&R方法:

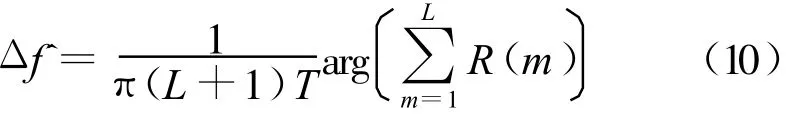
M&M方法:

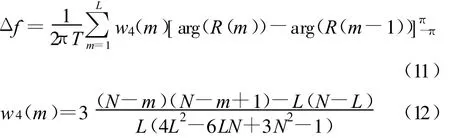
和基于接收信号差分的频偏估计方法相反,基于自相关函数的频偏估计方法的信噪比门限大大降低。Fitz和L&R方法的估计范围和估计精度相矛盾;M&M方法的估计范围不受到相关长度的影响,理想情况下可估计的归一化频偏达到(-0.5,0.5),和Fitz和L&R方法相比较,其信噪比门限稍高,但是远远小于L&W方法和Kay方法。

3 一种改进的Fitz载波频偏估计方法

对比Fitz方法和M&M方法可以看出,Fitz方法利用的是自相关序列R(m)的相位估计频偏,其估计范围和利用的自相关序列长度L有关,估计范围会随着L的增大而减少。而M&M方法利用的是自相关序列差分的相位,其估计范围与利用的差分序列的长度无关。仿照M&M方法,利用自相关序列差分估计频偏,修改Fitz方法的窗函数,增大其估计范围,将改进的Fitz方法称为Fitz-improved方法。表达式为

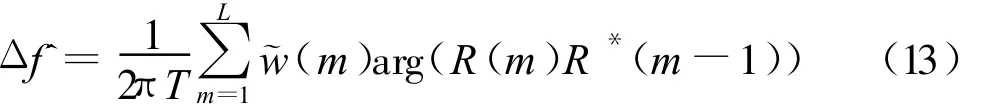
由式(13)得

根据式(8)和式(14)以及式(15)得到:

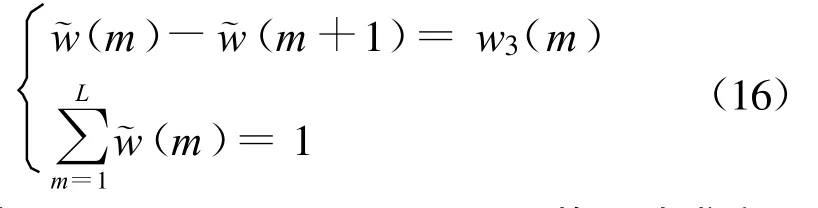
整理得到 w(m)= w(m+1)+w3(m),将两边求和:

整理得到:

根据式(14)得到:

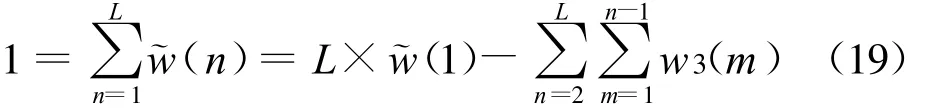
整理可得:

将式(9)中的 w3(m)代入式(20)得到:

通过利用自相关函数序列差分代替自相关函数序列估计载波频偏,使得其估计范围和自相关函数的长度无关,扩大了其估计范围,同时又保留了Fitz方法低信噪比门限的优点。

4 仿真分析

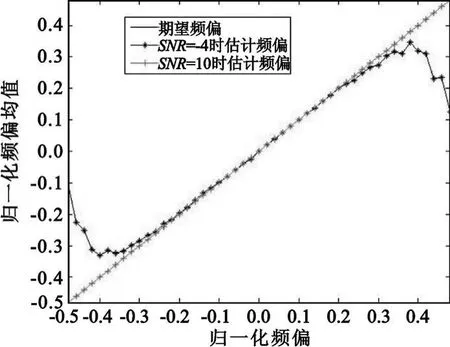
图1 Fitz-improved方法的频偏估计曲线Fig.1 Average of frequency estimation of Fitz-improved method

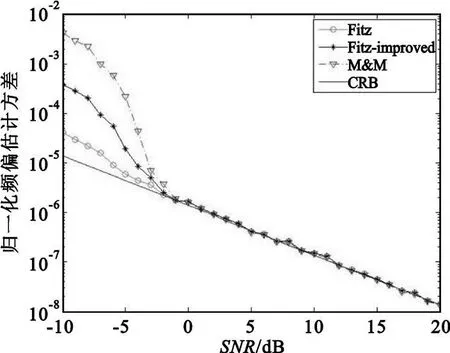
图2 Fitz-improved方法的归一化频偏估计方差Fig.2 Normalized estimation variance of Fitz-improved

下面考察数据长度N以及相关长度L对Fitzimproved方法的影响。图3为接收数据长度N对此方法估计性能的影响,此时相关长度L=N/2。可以看出,增加接收数据长度能够改善性能。

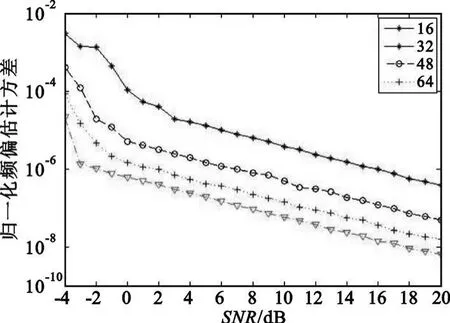
图3 数据长度对Fitz-improved方法的估计方差影响Fig.3 Impact of length of data on estimation variance of Fitz-improved

图4 为固定接收数据长度N,自相关函数的最大长度L对此方法估计性能的影响。从图中可以看出,当 L=N/2时,估计性能最优。

图4 自相关序列长度对Fitz-improved方法的估计方差影响Fig.4 Impact of length of autocorrelation sequences on estimation variance of Fitz-improved

5 结 论

通过对比分析现有经典频偏估计方法,本文给出了一种基于自相关函数的改进Fitz频偏估计方法。和原有的利用自相关函数的Fitz频偏估计方法相比,该方法由于利用自相关函数差分估计频偏,所以其频偏捕获范围和自相关函数的长度无关,捕获范围大,同时又保持了原有Fitz方法在低信噪比情况下估计精度高的优点,适用于大频偏和低信噪比下的载波频偏估计。

[1]Lovell B C,W illiamson R C.The statistical performance of some instantaneous frequency estimators[J].IEEE Transactions on Signal Processing,1992,40(7):1708-1723.

[2]Kay S.A fast and accurate single frequency estimator[J].IEEE Transactions on Acoustics,Speech,and Signal Processing,1989,37(12):1987-1990.

[3]Fitz M P.Further Results in the Fast Estimation of a Single Frequency[J].IEEE Transactions on Communications,1994,42(2/3/4):862-864.

[4]Luise M,Reggiannini R.Carrier frequency recovery in alldigital modems for burst-mode transmissions[J].IEEETransactions on Communications,1995,43(2/3/4):1169-1178.

[5]Umberto M,Morelli M.Data-Aided frequency estimation for burst digital transmission[J].IEEE Transactions on Communications,1997,45(1):23-25.

[6]Cao Yinwen,Yu Song.Frequency Estimation for Optical Coherent MPSK System Without Removing Modulated Data Phase[J].IEEE Photonics Technology Letters,2010,22(10):691-693.

[7]龚超,张邦宁,郭道省.基于FFT的快速高精度载波参数联合估计算法[J].电子学报,2010,38(4):766-770.GONG Chao,ZHANG Bang-ning,GUO Dao-xing.A quick and accurate union carrier parameter estimation algorithm based on FFT[J].Acta Electronica Sinica,2010,38(4):766-770.(in Chinese)

[8]Aboutanios E,Mulgrew B.Iterative Frequency Estimation by Interpolation onFourier Coefficiens[J].IEEETransactions on Signal Processing,2005,53(4):1237-1242.

[9]王成,吴瑛,韩广.基于自相关函数的前向载波频偏估计算法[J].计算机工程与设计,2010,31(17):3790-3792.WANG Cheng,WU Ying,HAN Guang.Feedforward carrier frequency offset estimator based on autocorrelation function[J].Computer Engineering and Design,2010,31(17):3790-3792.(in Chinese)

[10]刘世刚,葛临东.一种宽范围高精度的前向载波频偏估计算法[J].系统仿真学报,2008,20(18):4968-4970.LIU Shi-gang,GE Lin-dong.Feedforward Carrier Frequency Offset Estimator with Wide Range and High Accuracy[J].Journal of System Simulation,2008,20(18):4968-4970.(in Chinese)

[11]朱勇刚,姚富强,柳永祥.一种适用于低信噪比的ML载波频偏估计方法[J].系统工程与电子技术,2011,33(2):427-431.ZHU Yong-gang,YAO Fu-qiang,LIU Yong-xiang.ML-based carrier frequency offset estimation and its low SNR threshod[J].System Engineering and Electronics,2011,33(2):427-431.(in Chinese)

[12]张英龙,刘渝,王旭东.基于频偏校正的正弦波频偏估计方法[J].南京航空航天大学学报,2007,39(5):597-600.ZHANG Ying-long,LIU Yu,W ANG Xu-dong.Sinusoid Frequency Estimation Method Based on Frequency Offset Correcting[J].Journal of Nanjing University of Aeronautics&Astrouautics,2007,39(5):597-600.(in Chinese)

[13]帅涛,任前义,刘静,等.一种适用于大频偏和低信噪比条件的频率估计器研究[J].宇航学报,2010,31(12):2741-2745.SHUAI Tao,REN Qian-yi,LIU Jing,et al.An Frequency Estimator for Large Frequency Offset and low SNR Signals[J].Journal of Stonuautics,2010,31(12):2741-2745.(in Chinese)

[14]谭晓衡,张毛.一种高精度的改进FFT频偏估计算法[J].重庆理工大学学报(自然科学版),2010,24(7):71-75.TAN Xiao-heng,ZHANG Mao.Hign Accurate Frequency Offset Estimation Based on Modified FFT[J].Journal of Chongqing University of Technology(Natural Science Edition),2010,24(7):71-75.(in Chinese)