时间序列ARIMA模型在艾滋病疫情预测中的应用＊

罗 静，杨 书，张 强，王 璐

（1.四川大学公共卫生学院卫生统计教研室，成都 610041；2.成都医学院公共卫生系，成都 610083）

艾滋病，即获得性免疫缺陷综合征（acquired immune deficiency syndrome，AIDS），是由艾滋病病毒（HIV）破坏人体免疫系统，使其丧失抵抗各种疫病能力的一种严重危害人类生命安全的疾病。2000年以后，特别是2005年以来，中国的艾滋病感染人数迅速上涨。在艾滋病的防控工作中，如果能在局部范围内对未来感染人数做一定程度预判，为“三间分布”提供信息，对制定正确的防控政策和卫生资源配置提供依据，具有一定的指导意义。本文以重庆市疾病控制部门提供的艾滋病疫情发展为例，采用求和自回归移动平均（auto regressive integrated moving average，ARIMA）时间序列模型拟合预测发病率，探讨模型的可行性，对相关问题进行探索性研究。

1 资料与方法

1.1 一般资料 相关数据由重庆市疾病控制部门提供，包括1993～2009年重庆市辖区月度新发艾滋病感染人数，以及该市2010年卫生统计年鉴。

1.2 模型建立 ARIMA模型是以序列不同时期内的相关度量为基础进行的一种精确度较高的短期预测分析方法。该法由美国学者Box和英国统计学者Jenkins于1976年提出，故又称为Box－Jenkins模型［1］。在ARIMA模型中，变量的未来取值可以表达为过去若干个取值和随机误差的线性函数。

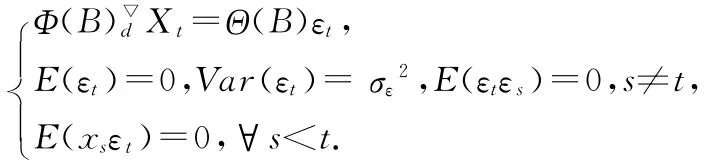
式中：

▽d＝（1－B）d

Φ（B）＝1－φ1B－…－φpBp

Θ（B）＝1－θ1B－…－θqBq

其中B是后移算子，εt为各期的随机扰动或随机误差，d为差分阶数，p和q分别表示自回归阶数和移动平均阶数，Xt为各期的观察值（t＝1，2，…，k）［2－3］。

建立ARIMA时间序列模型可归纳为3个阶段，即序列的平稳化、模型识别以及参数估计和模型诊断，通过这3个阶段处理的反复进行，最终确定一个用于预报的“最优”模型［4］。

1.2.1 序列的平稳化 序列的平稳性是ARIMA模型分析的前提条件，即要求均数不随时间变化；方差不随时间变化；自相关系数只与时间间隔有关，而与所处的时间无关［5］。对于非平稳的序列，可以通过差分和Box－Cox变换使均数和方差平稳化。

1.2.2 模型识别 通过观察序列自相关（auto correction fuction，ACF）和偏自相关（partial auto correction fuction，PACF）的截尾、拖尾性初步为序列定阶，提供几个粗模型以便进一步分析完善［6－7］。

1.2.3 参数估计和模型诊断 根据模型阶数，运用最大似然法估计或最小二乘法估计，计算出求和自回归移动平均过程的各项系数，并做假设检验。在模型的拟合中，应满足模型的残差序列是白噪声序列，即Box－Ljung Q统计量相比较差异无统计学意义（P＞0.05）。若几个模型均满足参数相比较差异有统计学意义，残差序列为白噪声序列的要求，则使拟合优度统计量赤池信息准则（akaike’s information cnitenion，AIC）和贝叶斯算法（selective bayes classifiers，SBC）均达到最小的模型为最优模型。反之，模型参数间比较差异无统计学意义，或残差序列不是白噪声序列，都需要返回识别阶段，重新调整各个阶数的值，再进行参数估计和模型诊断。

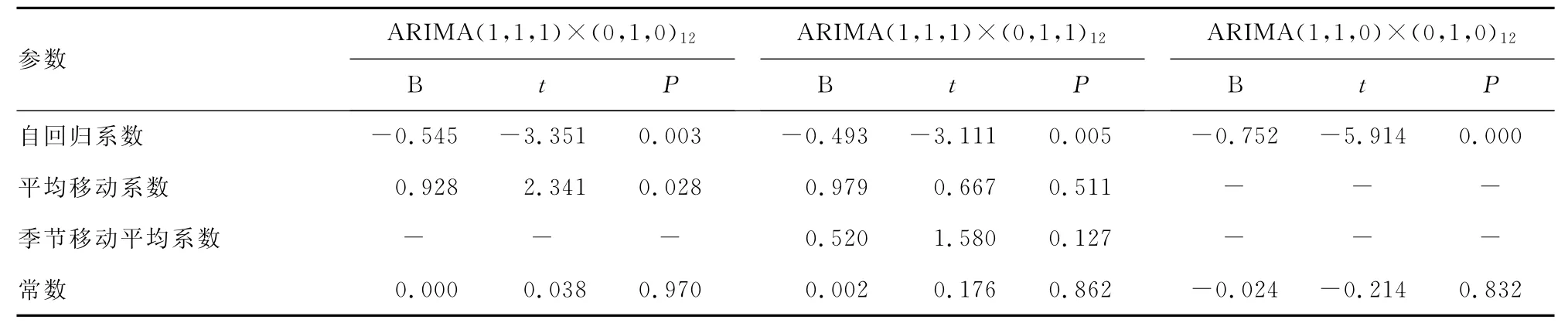
表1 备选模型的参数估计

1.3 统计学处理 应用SPSS 13.0统计软件建立ARIMA时间序列模型并进行数据处理和分析［8－9］。

2 结 果

2.1 数据处理 对1993～2009年重庆市疾病控制部门提供的艾滋病月发病率作序列图，发现数据总体呈上升趋势。其中，1993～2003年月发病率较低，其大多数月份为0，最大值为0.073 9（1／10万）；2005年1月和3月呈现2个高峰，其后数据波动幅度增大，序列的方差在前后差别明显。因此，以2005年1月为切点，将数据分为两个部分。以2005年1月至2009年6月发病率作建模数据，2009年7～12月的数据作验证数据，对序列进行自然对数变换，差分和季节差分后，序列平稳。

2.2 模型识别 观察处理后序列的ACF和PACF（图1、2），发现自相关函数和偏自相关函数呈现递减且拖尾。可初步判断模型为模型一 ARIMA（1，1，1）×（0，1，0）12、模型二 ARIMA（1，1，1）×（0，1，1）12或模型三 ARIMA（1，1，0）×（0，1，0）12。

2.3 参数估计及检验 模型一和模型三的参数间比较差异有统计学意义，模型二中MA1和SMA比较差异无有统计学意义。见表1。

2.4 模型诊断 表2所示，在备选模型中，模型一拟合优度较小，且参数间无明显相关性（r＝0.267）。此外，观察其残差的自相关图，结果显示该模型的Box－Ljung Q统计量间比较差异均无统计学意义（P＞0.05），可以认为残差序列为白噪声［10］。综上分析，模型一为最优模型。可以确定重庆市艾滋病发病率的预测模型为 ARIMA（1，1，1）×（0，1，0）12，其表达式为：（1＋0.545B）▽12▽lnXt＝（1－0.928B）εt。

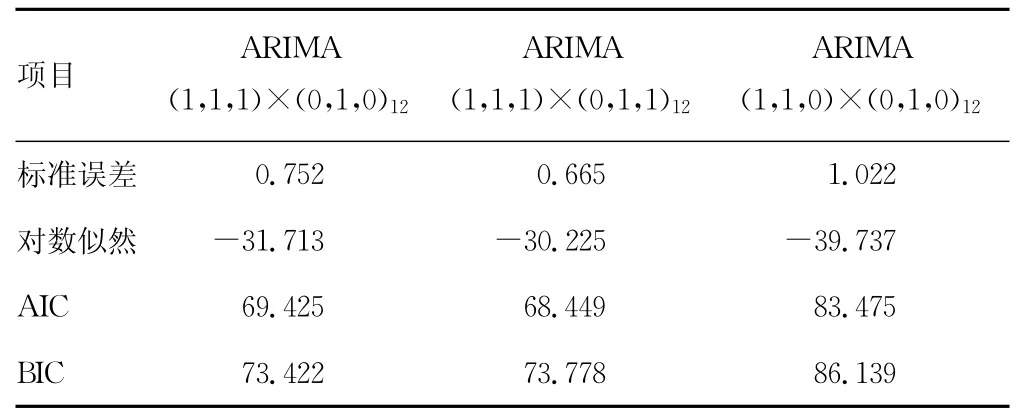
表2 备选模型拟合优度统计量

2.5 模型预测 用 ARIMA（1，1，1）×（0，1，0）12模型预测重庆市2009年7～12月艾滋病发病率，结果如表3所示。可以看出模型预测值的动态趋势与实际情况基本一致，模型对未来的情况进行了很好的跟踪和预测。2009年7～12月的实际发病率虽然与预测值不完全一样，但是各月实际值都落入了预测值95%的可信区间范围。

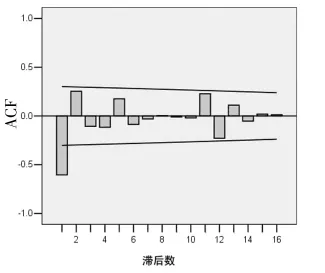
图1 原序列经过对数转换和两次差分后的ACF图

表3 2009年7～12月重庆市实际发病率与预测发病率（1／10万）

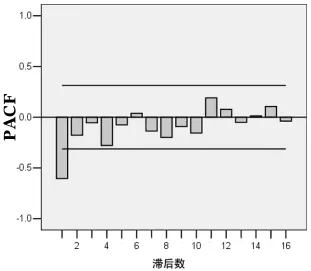
图2 原序列经过对数转换和两次差分后的PACF图

3 讨 论

3.1 艾滋病发病率预测的意义 根据模型预测并结合实际情况，重庆市艾滋病感染速度呈上升趋势。相关部门可以有针对性地采取预防控制措施。如整合艾滋病医疗资源，大力提升其诊治能力；建立“重庆市艾滋病关爱之家”［11］，动员全社会参与艾滋病防治，消除对艾滋病患者的恐惧和歧视；组建艾滋病职业暴露药品库，降低全市艾滋病职业暴露人员感染HIV的危险性等［12］。由于近几年重庆市艾滋病感染者基数较大且不断增加，致使发病率仍然不断上升，所以，还应加大其预防控制工作强度并且在预防控制手段上有所创新，加大对高危人群及高发地区的监测和行为干预［13］。

3.2 ARIMA模型的应用 时间序列分析是在不需要考虑预测变量的相关因素及其关系的情况下，利用事物发展的延续性，建立时间序列模型来预测未来的变化［14］。而传统的时间序列模型要求序列具有平稳的线性趋势，但实际上疾病的发病情况一般有着明显的周期变化，如果不考虑这些因素的影响，做出的预测往往不准确。本研究采用的ARIMA模型，综合考虑了序列的趋势变化、周期变化及随机干扰等因素的影响，对艾滋病发病拟合度较好［15］。由于疫情波动受到诸多未知随机因素的影响，所建立的模型不是一成不变的，它较适合进行短期的预测，同时需要不断加入新的实际数据，以不断新拟合更能反映实际情况的预测模型，并提高预测的敏感性。

［1］ Geoge EP，Gwilym M.时间序列分析预测与控制［M］.北京：中国统计出版社，1997.

［2］ 肖枝洪，郭明月.时间序列分析与SAS应用［M］.武昌：武汉大学出版社，2009.

［3］ 何书元.应用时间序列分析［M］.北京：北京大学出版社，2003.

［4］ 孙振球，徐勇勇.医学统计学［M］.北京：人民卫生出版社，2002.

［5］ 张文增，冀国强，史继新，等.ARIMA模型在细菌性痢疾预测预警中的应用［J］.中国卫生统计，2009，26（6）：636－639.

［6］ 吴家兵，叶临湘，尤尔科.时间序列模型在传染病发病率预测中的应用［J］.中国卫生统计，2006，23（3）：276.

［7］ 刘晓宏，金丕焕，陈启明.ARIMA模型中时间序列平稳性的统计检验方法及应用［J］.中国卫生统计，1998，15（3）：12－14.

［8］ 张文彤.SPSS11统计分析教程高级篇［M］.北京：北京希望电子出版社，2002.

［9］ 薛薇.SPSS统计分析方法及应用［M］.2版.北京：电子工业出版社，2009.

［10］孟蕾，王玉明.ARIMA模型在肺结核发病预测中的应用［J］.中国卫生统计，2010，27（5）：507－509.

［11］王治伦，晏治碧，陈思源，等.建立重庆市艾滋病关爱之家体会［J］.中国感染控制杂志，2004，3（3）：275－276.

［12］李颖，汪洋，刘琴，等.重庆市高危人群中艾滋病防治的定性研究［J］.中国卫生事业管理，2005（2）：96－97.

［13］丁贤彬，邝富国，凌华，等.重庆市艾滋病流行现状及防治策略［J］.疾病控制杂志，2005，9（4）：340－341.

［14］邓丹，王润华，周燕荣.时间序列分析及其在卫生事业中的应用［J］.数理医学杂志，2002，15（5）：455－457.

［15］冯超，白彬.时间序列模型拟合艾滋病发病趋势预测［J］.中国公共卫生，2005，21（7）：893.