Theoretical Studies in Isolated Prop Model of Subsea Pipeline
LIU Yu-xiao,GE Tao,SONG Hua-ling
(1 Dept.of Management Science and Engineering,Shandong Institute of Business and Technology,Yantai 264005,China;2 State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116023,China;3 Shandong Institute of Business and Technology,Yantai 264005,China)
1 Introduction
More and more high temperature and high pressure(HT/HP)pipelines are being used in the development of deep water and marginal oil fields.A submarine pipeline laid on or under the seabed and operated at pressure and temperature above ambient will result in expansion[1].When the axial compressive force is large enough that pipeline will buckle globally.For buried pipeline,upheaval buckling will be triggered;for pipeline exposed on even seabed,lateral buckling will be observed[2].
Hobbs[3-4]studied the thermal buckling of pipeline induced by the transportation of high temperature fluid.He used perfect pipe and the model of small deflection beam-column on rigid foundation to analyze the thermal buckling behaviors of beam vertical mode and beam lateral mode.Taylor and Tran[5]studied upheaval buckling of subsea pipeline experimentally and theoretically.Several researchers have investigated the effects of initial imperfections,but the curved pipe was assumed to be stress-free when initially deformed.Croll[6]studied upheaval thermal buckling of subsea pipeline based on a simplified model,critical buckling force was derived,but,the pre-buckling force was not given.Liu Yuxiao[7]studied lateral buckling of imperfect pipeline,and critical axial forces in buckling segment and away from buckling segment as well as critical temperature are deduced.
In the paper,isolated prop model of pipeline was studied;critical upheaval buckling length,upheaval buckling force and pre-buckling force are derived.
2 Critical upheaval buckling length
An important class of imperfection is that resulting when an otherwise straight pipe rests upon an isolated prop as shown in Fig.1(a).If the amplitude of this protrusion is Vom,it is a simple matter to show that the natural wavelength of the suspended portion would be given[5]by:

Under the action of an increasing axial load P there will be a gradual shortening of the suspended span,as shown in Fig.1(b),and an associated reduction in the point reaction at the point support.Upheaval is deemed to occur when wavelength L has reduced from L=Lito some value L=Lu,and the point reaction at the point support is zero.
(a)Datum(p=0)
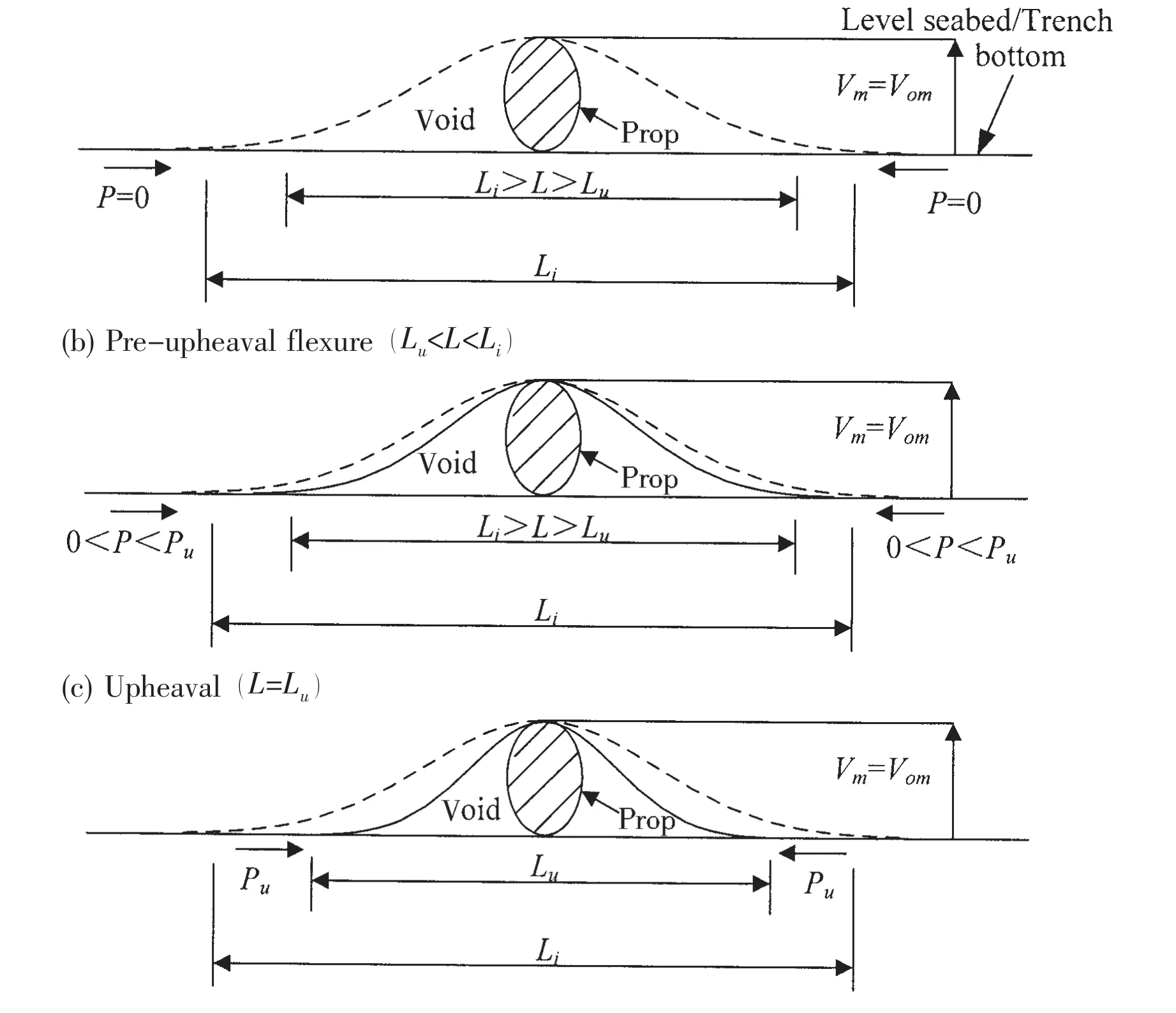

Fig.1 Upheaval shape of pipeline
For the upheaval buckling mode,the buckled part of the pipeline is treated as a beam-column under uniform lateral load equal to the pipe self-weight.It is assumed that the bending moment at the lift-off point is zero and the slope is small so that linear equations related to column buckling are appropriated.Referring to Fig.1(c),for the upheaval buckling mode,a free-body diagram of a segment from the buckled part at the right lift-off point is obtained,as shown in Fig.2.
The external moment acting on the cut section is
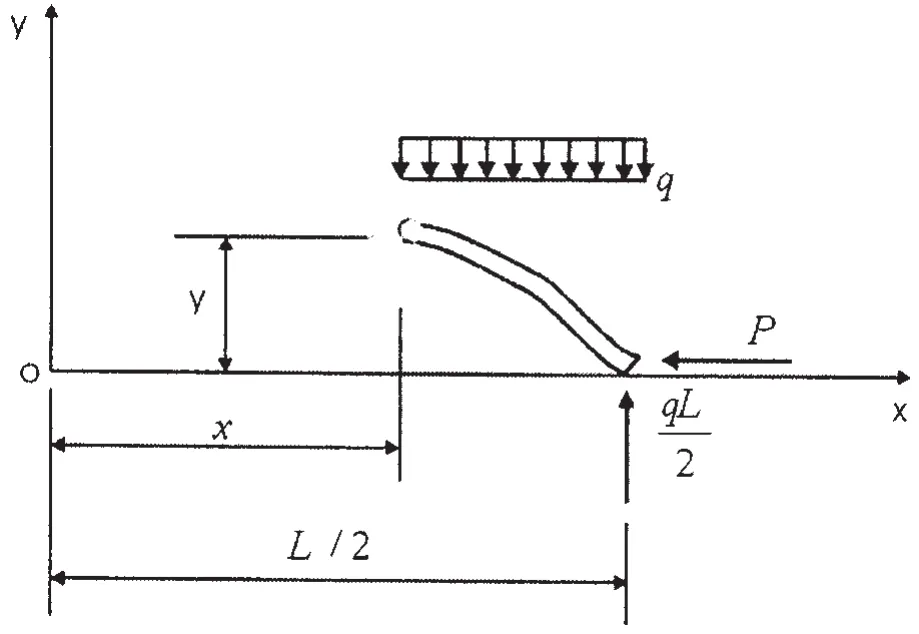
Fig.2 Upheaval shape of pipeline
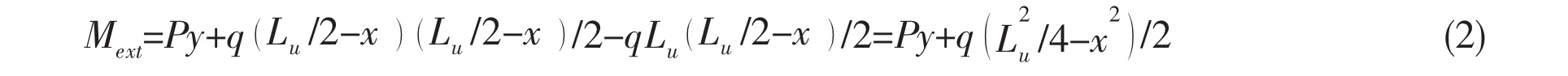
and the internal moment is:

For equilibrium,Mint=Mext.Substituting Eq.(3)into Eq.(2),the following relationship can be obtained:

where y is the lateral displacement of initial imperfection with respect to the longitudinal coordinate x,q is the pipe self-weight(force per unit length),and the moment of inertia is I,m=q/EI,n2=P/EI,and Luis the critical upheaval buckling length between the lift-off points.The solution of equation(4)is:
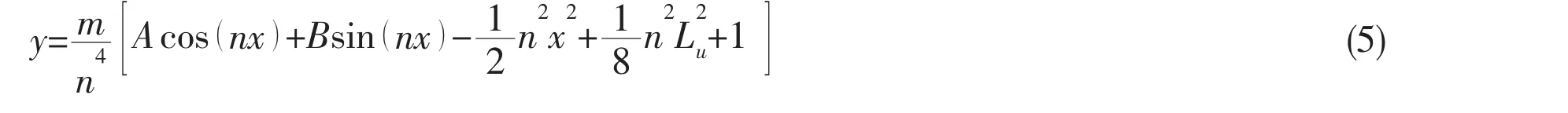
where A and B are unknown constants and can be solved from the boundary conditions.
Using the boundary conditions that y′=0,)=0,y′0,the solution for Eq.(5)becomes:
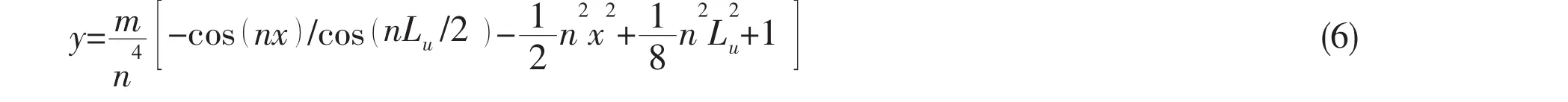
The unknown length of buckle Luis then determined from the condition that the slope at the ends of the buckled should be zero.This yields:

which has the lowest non-trivial root:

So the deflected shape for the pipe segment becomes:
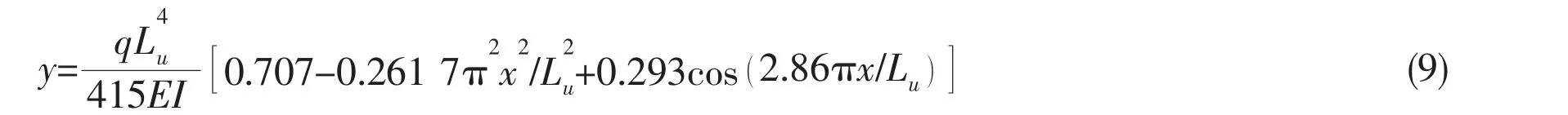
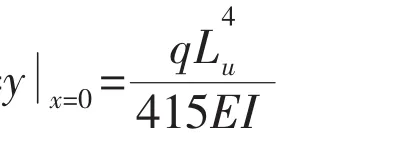
then

Combing Eq.(1),then:

3 Upheaval buckling force of pipeline
3.1 Fundamentals
The maximum effective axial force in a completely constrained pipeline lying on the seabed subject to temperature and internal pressure can be expressed as[3,5,8-9]:

where P0is the pre-buckling force;A is the net cross-sectional area of the pipeline;E is the elastic modulus of steel pipe;α is the coefficient of linear thermal expansion;T is the temperature;ν is the Poisson’s ratio;p is the internal pressure;D is the outer diameter;t is the wall thickness of the pipe.
Merging the known action parameters T and p leads to computational convenience such that Eq.(1)can be written as:

where T′is defined as the corresponding temperature due to pressure;ΔT the equivalent temperature rise due to both temperature and pressure.
Critical buckling force[10-11]of a beam under uniform lateral forces can be determined on the base of the theory of Euler global buckling.

where λ is the length coefficient related to end restriction;λL1the equivalent length of the original compressed bar.
3.2 Upheaval shape of pipeline
Combined with the engineering application,in practical engineering initial imperfections exist even for subsea pipeline installed on even seabed.Upheaval shape is illustrated in Fig.3 and expressed as[6,12].

where yuis the lateral displacement of initial imperfection with respect to the longitudinal co-ordinate x;Vomis isolated prop height,Vom=,Luis the length of initial imperfection.
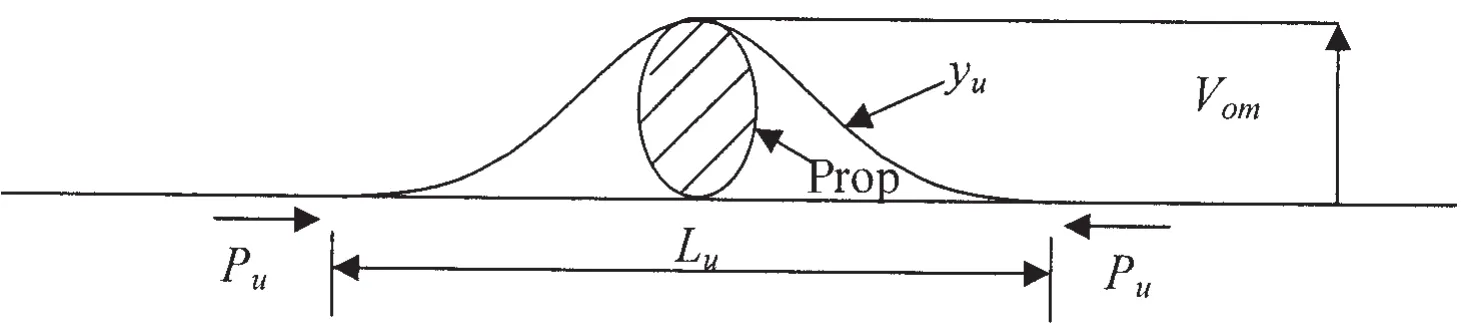
Fig.3 Upheaval shape of pipeline
3.3 Critical upheaval buckling force
A free-body diagram of a buckled pipeline is shown in Fig.4.The bending moment at the ends of equivalent length is zero,then

the equilibrium equation of bending moment can be established as
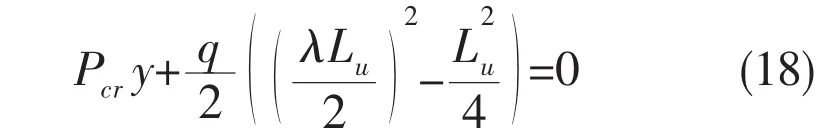
Combining Eqs.(10),(15)and(16),Eq.(18)becomes:


Fig.4 Sketch of buckled pipeline
Thus,Eq.(19)has the solution:λ=0.388.
Then,upheaval critical buckling force in buckled pipe can be taken as:

3.4 Pre-buckling force of pipeline
Axial force distribution[4-5,12]is illustrated in Fig.5.The pipeline is composed of buckled segment,slip segment and full constrained segment.

Fig.5 Axial force distribution
Presuming fully mobilized friction resistance to be developed,the model definition is completed by means of compatibility expression[13].
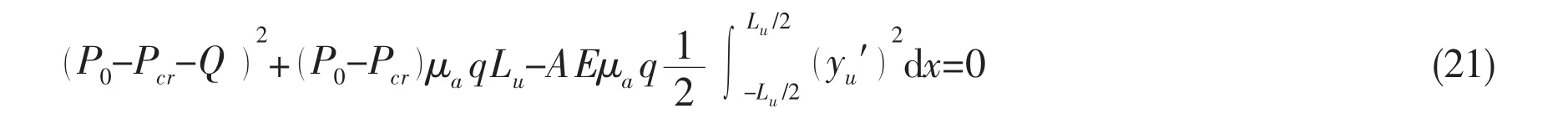
where μais the axial friction coefficient between the pipeline and the seabed,Lsthe slip length,Q=μaqLu/2.
Combining Eq.(16)yields
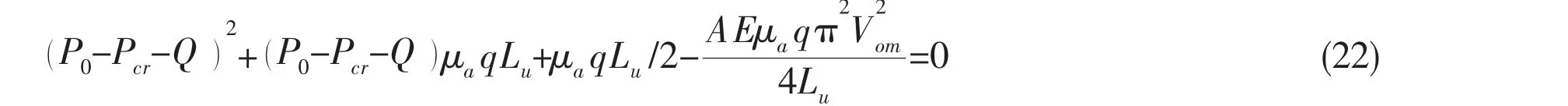
then,

Finally,from Eq.(13),critical buckling temperature of imperfect pipeline takes the form
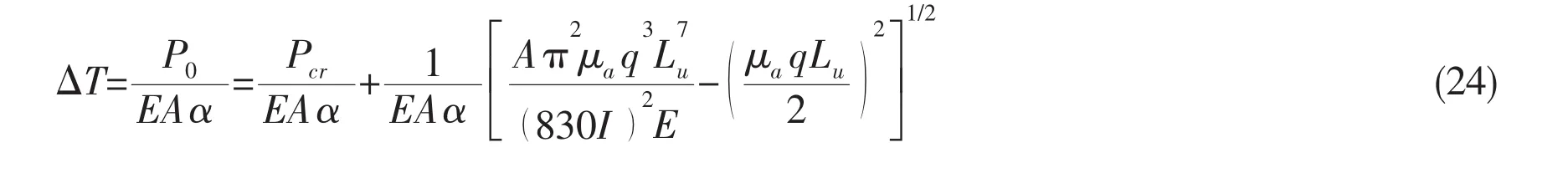
4 Comparisons
For the pipeline considered by Taylor and Tran,Fig.6 shows the buckle force at upheaval.The considerable differences could be due to the assumption made in Ref.[5],that the out-ofstraight pipeline under no axial load is stress free.

Fig.6 Finite element model of pipeline
5 Conclusions
Isolated prop model of submarine pipeline is studied analytically.Closed-form solutions to critical axial forces in buckling segment,pre-buckling axial force and critical temperature rise are proposed.Comparison of results between the solution presented in the paper and Taylor’s solution shows that imperfection has significant effect on upheaval critical buckling forces of pipeline.
This research is financially supported by the National Natural Science Foundation of China(No.50439010),the Natural Science Foundation of Shandong Province(ZR2011DL004),the Opening foundation of State Key Laboratory(LP1115),Humanity and Social Science Foundation of Ministry of Education(11YJA630101).These supports are greatly appreciated.
[1]Allwood R L.Global buckling of submarine pipelines[D].Florian,Cranfield University,2007.
[2]DNV-RP-F110.Global buckling of submarine pipelines structural design due to high temperature/high pressures[S].Det Norske Veritas,Norway,2007.
[3]Hobbs R E.In-service buckling of heated pipeline[J].J Transport Eng,1984,110:175-189.
[4]Hobbs R E,Ling F.Thermal buckling of pipelines close to restraints[C]//Proceedings of the 8th International Conference on Offshore Mechanics and Arctic Engineering.Hague,1989:121-127.
[5]Taylor N,Tran V.Experimental and theoretical studies in subsea pipeline buckling[J].Marine Structures,1996,9:211-257.
[6]Croll J G A.A simplified model of upheaval thermal buckling of subsea pipelines[J].Thin-Walled Structures,1997,29:59-78.
[7]Liu Yuxiao,Li Xin,Zhou Jing.Analytical studies of imperfect pipelines on lateral buckling[J].Journal of Ship Mechanics,2011,15(9):1033-1040.
[8]Taylor N,Gan A B.Regarding the buckling of pipelines subjected to axial loading[J].J Constructional Steel Research,1986,4:45-50.
[9]Taylor N,Gan A B.Submarine pipeline buckling-imperfection studies[J].Thin-Walled Structures,1986,4:295-323.
[10]Li Y X.Critical length of thermal buckling bar[J].Journal of Southwestern Petroleum Institute,1993,15(1):90-91.
[11]Sun X F,Fang X S,Guan L T.Material mechanics[M].Beijing:Higher Education Press,1985.
[12]Nader Y G.Analysis of buried pipelines with thermal applications[D].Master thesis.Canada,University of Alberta,2002.
[13]Song X J.Numerical solutions for pipeline wrinkling[D].Canada,University of Alberta,2003.
- 船舶力学的其它文章
- Activities of Propulsion Design and Cavitation Test for Merchant Ships in CSSRC
- 3D Trajectory Tracking Control Platform Design for Deep Sea Open-framed Remotely Operated Vehicle based on Hydrodynamics Test
- Quasi-static Compressive Behavior of U-type Corrugated Cores Sandwich Panels
- Structural Dynamic Response Study of Large LNG Carriers under Sloshing Impacts in Tanks
- Research of Repair Major Joint Cracks of Offshore Platforms by Finite Element
- An Application of Homogeneous Matrix Method of Multi-body System to the Dynamic Response of Floating Bridge

