基于FFT-FS频谱细化技术的船模耐波性试验测量信号分析方法研究

许 勇，董文才，欧勇鹏

（海军工程大学 船舶与海洋工程系，武汉 430033）

1 引 言

在耐波性系列模型试验（如滑行艇艉底斜升角变化对船模运动响应影响的试验研究）及一些非常规试验（如气泡高速艇喷气后形成的气层对其运动响应影响的试验研究）中常常需要捕捉研究对象参数的细微变化对运动响应的影响，但由于试验测量信号中存在很多干扰（如测量设备本身的高频电噪声、仪器调零误差带来的低频趋势项、拖车在行进时本身的抖动、二次试验间隔时间不够而残留的小波的干扰等），使得所研究对象参数变化对运动响应的影响往往淹没在这些干扰因素中，要识别这些细微变化则必须采用高精度的信号分析方法。而船模对波浪的运动响应是低频的且是窄频带[1]，所以对该窄带频段进行频谱细化处理则可望得到这些细微的变化。

FFT分析是一种使用最为广泛的频域分析方法。该方法能得到整个频段上的频谱信息，但是其受到频率分辨率的限制。所谓频率分辨率[2]Δf即为采样频率fs与FFT变换点数N1的比值，根据频率与圆频率的关系则可得圆频率分辨率为Δω=2πΔf。而FFT变换点数N1又与采样点数N存在如下换算关系[3]

其中[]为取整符号。因此频率分辨率和信号的采样点数及传感器采样频率有关，实质上与采样时间有关。而船模的耐波性试验一般都在拖曳水池中进行，水池长度有限导致总的采样时间不长，所以若采用FFT分析则频率分辨率受到限制，这也将影响其它表征信号频域特征量（如幅值、相位、功率谱密度等）的分析精度。当然，可以采用补零的方法来增加数据的长度以提高FFT分析的频率分辨率，但频率分辨率每缩小一倍则数据长度要增加一倍，这会引起运算量和存储量的急剧增加，而FFT也将失去其快速性算法的意义。所以一种频率分辨率高、运算速度快且具有局部分析功能的频域方法将有助于船模耐波性试验测量数据的处理和分析。

为了提高频率分辨率，捕捉信号更详细和精确的频幅特性，出现了不少的频谱细化方法[2,4-5]，如复调制ZFFT，相位补偿细化，AR谱局部表示法等。复调制ZFFT以及相位补偿细化[4]在一定程度上能提高频率分辨率，但所需的数据量也成倍地增加，对于原始数据长度恒定或瞬变信号进行细化分析时，上述方法显然无能为力，并且分析前要先对信号进行频移和低通滤波[4]，这不仅增加了信号处理的难度，而且降低了信号分析的效率，不利于实现信号的实时处理。AR谱等现代谱分析方法[5]，由于是连续谱图，故不受采样点数的影响，在理论上频率分辨率可以达到无穷小，但由于建模方法和模型阶次确定的差异会产生谱线偏移和谱线分裂现象，得不到非常准确的频率值。FFT-FS频谱细化技术[2]，在不增加数据长度的前提下利用傅立叶级数的原理得到连续的频谱曲线，不仅可以消除频率分辨率的限制，还能克服上述方法的不足。本文尝试采用该方法来获得船模运动响应信号的细化谱。

2 FFT-FS算法原理

FFT-FS实际上是一种联合采用快速傅立叶变换（FFT）及傅立叶级数展开（FS）的信号处理方法。其原理是在不增加数据长度N的前提下对信号先进行N1点（见（1））式FFT，初步确定信号的频幅特性，然后对FFT的离散频率通过变量代换获得连续频率，并对感兴趣的局部频段进行傅立叶级数展开获得连续的频谱曲线。关于频率的变量代换、FFT-FS、FFT更详的介绍可参考文献[2-3]。对于船模实测耐波性运动响应信号来说，感兴趣的频段是遭遇圆频率ωf附近的局部频段，该频段内的傅立叶级数展开式（细化谱）为

其中:x（n）为实测时间序列，N为采样点数，fs为采样频率，ω 为圆频率，dω 为细化频段的半宽，[ωf-dω,ωf+d ω ]为离散的频段；ω 处幅值谱矢量表达式为a（ω）+jb（ω），幅值大小为A（ω）=（ω）+b2（ω）。因此根据（2）式则可以得到频段 [ωf-dω,ωf+dω ]内的连续的细化幅值谱。

但在程序实现时，仍需对ω进行离散，设N3为频段 [ωf-dω,ωf+dω ]内离散的点数（一般称N2为离散的谱线数），此时频率分辨率为Δω=2dω/N2。故通过上述方法可以得到分辨率为Δω的频幅特性曲线，且调节谱线数目N′可获到不同分辨率时的幅值谱。

3 FFT-FS算法的运算量分析及与FFT的比较

对采样点数为N的实测序列采用FFT-FS分析时，其运算量包括进行N1点FFT的运算量和进行傅立叶级数展开求N2条细化谱的运算量。

对采样点数为N的实测时间序列x（n）采用FFT-FS分析时，其运算量包括进行N1点FFT的运算量和进行傅立叶级数展开求N2条细化谱的运算量:由文献[3]给出的估算公式并根据复数运算和实数运算之间的关系可得进行N1点FFT需要进行实数加法为2.5N1log2（N1）次，实数乘法为N1log2（N1）次；根据（2）式可知计算N2条细化谱需要进行的实数加法为2NN2次，实数乘法为2NN2次，因此FFT-FS的实数加法为Sa=2NN2+2.5N1log2（N1）次，实数乘法为Sm=2NN2+N1log2（N1）次。若采用FFT分析要得到和FFTFS同样分辨率Δω的幅值谱，则需要进行FFT变换的数据长度为M=πfsN1/dω，根据（1）式可求得进行FFT 的点数为 M′=2[log2（M）]次，则需要进行的实数加法为Sa=2.5M′log2（M′）次，实数乘法为Sm=M′log2（M′）次。

图1给出了采样点数N不同时FFT-FS、FFT乘法运算量随分辨率的变化关系（加法运算量变化规律和此类似），其中采样频率为200Hz，细化频段的半宽为1。从图中可以看出:（1）在分辨率相同时，FFT-FS的运算效率要高于FFT算法，尤其是在高分辨率时FFT-FS的运算效率明显要高于FFT运算效率；（2）当实测信号的采样点数N增加时，FFT-FS运算量的优势逐渐减弱，也就是说当采样数据较多时，两者的运算量相当，而当采样点数较少时，FFT-FS的运算速度比FFT更有优势。第1节指出船模耐波性试验测量数据受采样时间的限制而导致采样点数有限，因此采用FFT-FS对这些信号进行分析则能发挥其运算速度快的优势。

4 FFT-FS算法的精度分析

图1 FFT-FS、FFT的乘法运算次数随分辨率的变化Fig.1 Multiplicaiton operation number curves of FFT and FFT-FS at different frequency

4.1 FFT-FS、FFT计算精度的比较

根据文献[1]提供的数学模型，可以用单个或若干个正弦波的迭加来模拟船模在规则波和不规则波中的运动响应。而实测船舶耐波性运动响应信号中往往包含着噪声，可用高斯白噪声gwn（white Gaussian noise）来模拟，其中高斯白噪声对正弦信号的影响程度则可以通过信噪比snr（signal-to-noise ratio）来调节。关于信噪比和高斯白噪声更详细的介绍可以参见文献[6-8]。下面以两个仿真信号S1和S2来模拟船模的运动响应，S1和S2的表达形式如下:

其中时间t=0～20.48 s，采样频率为200 Hz，信噪比snr为1，幅值Ai、圆频率 ωi及相位 εi（i=1～6）的值如表1所示。S1模拟规则波激励时的垂荡响应，S2则模拟不规则波激励时的垂荡响应，两个仿真信号的时历过程如图2所示。

表1 仿真信号各正弦波特征参数Tab.1 Characteristic parameters of the simulation signals S1 and S2

图2 仿真信号的时历过程Fig.2 History curves of the two simulation signals

采用FFT-FS方法对S1和S2的遭遇频率ωf附近频段进行频谱细化处理，其中S1的细化频段半宽为1，细化谱线数为50，S2的细化频段半宽为2，细化谱线数为100，同时还对两个仿真信号进行了4096点的FFT分析，两种分析方法所得结果如图3所示:对比FFT和FFT-FS的幅频曲线可以看出FFT-FS的幅频曲线反映的幅频信息更丰富和细致，如S2的FFT-FS幅频曲线中可以清晰地看到5个子波的幅值谱（图中阿拉伯数字1～6标出了各子波对应的幅值谱），这和事实是相符的，而S2的FFT幅频曲线中只能看到4条这样的幅值谱，子波2和子波3的幅值谱线在图中无法分辨出来，其原因在于FFT受频率分辨率的限制，而子波2和子波3的频率又比较接近，所以FFT分析无法分辨出来。

图3 仿真信号的FFT幅值谱及FFT-FS幅值谱Fig.3 Amplitude-frequency curves of FFT and FFT-FS about the signals

为进一步比较FFT-FS、FFT的分析精度，表2统计了图3中各子波的幅频参数值。FFT分析结果中关于子波2的数据由于该方法分析失效，用“-”表示。对比表2和表1中的理论值可以知道:（1）由FFT分析得到的四个子波的频率误差分别在5%左右、而对应的幅值误差和相位误差却很大（如子波3的幅值误差达到34.519%，相位误差达到了132.486%），其原因在于采用FFT分析时计算的仅是频率为整数倍频率分辨率时的幅值，而两相邻整数倍频率分辨率之间的幅值无法求得，但两相邻整数倍频率分辨率之间存在着丰富的信息细节，因此出现频率的一点偏差将会带来幅值上很大的误差；（2）采用FFT-FS的频谱细化技术所得频率、幅值及相位和理论值相当接近，且误差都在3%之内，这也验证了该方法的有效性。综合上述的分析可以知道FFT-FS方法能够准确而且细致地描述信号的幅频特性，且是一种比FFT更有效的频域方法。

表2 仿真信号各子波的FFT、FFT-FS频幅参数统计Tab.2 Amplitudes,frequencies and phases of the two signals calculated by FFT and FFT-FS

4.2 细化谱线数对FFT-FS分析精度的影响

在同样宽度的频段内对信号进行频谱细化时，细化谱线的数目N2不仅决定了FFT-FS的运算量，而且还决定着细化谱的分辨率，从而也就决定了对信号分析的精度,因此选择合适的细化谱线数既能确保FFT-FS有好的分析精度又有高的运算效率。仍以S1为例，采用FFT-FS算法对该仿真信号的ωf附近dω为1的频段分别进行谱线数目为10、20、50、100及500的细化处理，其中仿真信号的信噪比snr为1，所得细化谱如图4所示。由图可知细化谱线数为50、100和500时的细化谱基本上是重合的，这说明当频段半宽dω1时选择谱线数为50就能得到满意的精度。

4.3 信噪比对FFT-FS分析精度的影响

船模耐波性试验测量的运动响应信号中含有噪声的影响，有的运动响应测量信号信噪比较小，如在短波激励时测得的加速度信号，而有的运动响应测量信号信噪比较大，如长波激励时的位移信号。因此研究FFT-FS分析精度是否受信号本身信噪比的影响及受到的影响究竟有多大则能考察该方法的普遍适应性。仍以S1为例，设定其信噪比snr分别为1、5和100，得到3个不同的信号，对这3个信号进行FFT-FS频谱细化，其中细化谱线数N′为50，细化的频段仍为仿真信号的ωf附近dω为1的频段，所得细化幅值谱如图5所示，由图可知这3条曲线基本上是一致的，这说明FFT-FS分析精度受信号本身信噪比snr的影响很小，即使是对强噪声背景下的测量信号（如snr为1时的信号）进行分析也能确保精度，因此该方法可以用于对船模耐波性试验数据的频谱细化分析。

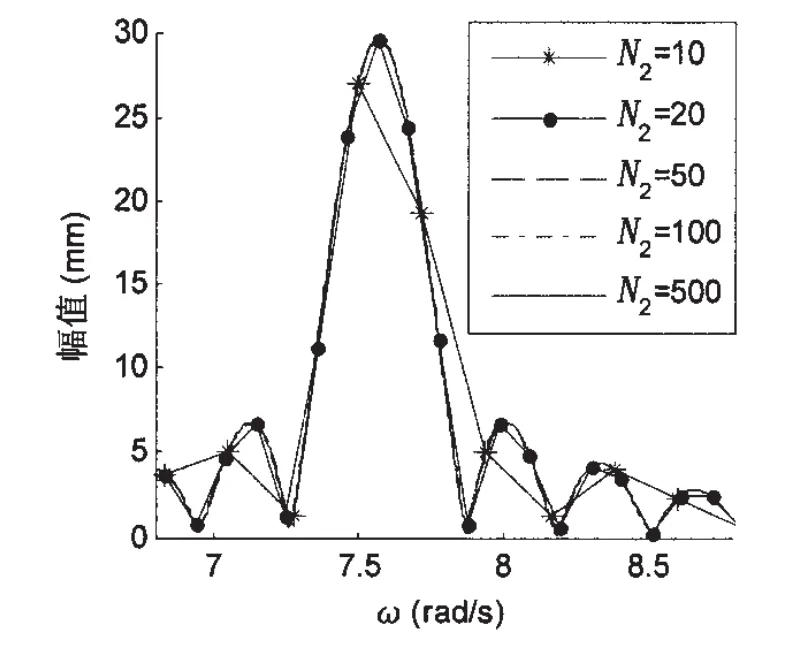
图4 不同N2时的细化谱比较Fig.4 Amplitudes-frequency curves of different N2 calculated by FFT-FS

图5 不同信噪比时的细化谱比较Fig.5 Amplitudes-frequency curves of different signal-noise ratio calculated by FFT-FS

5 船模耐波性实测信号的FFT-FS实例分析

在605所高速水动力试验室水池中对气泡高速艇模型sm8进行了耐波性试验，激励波为规则波、波长范围为2～13 m、名义波高60 mm，航速为固定航速6.124 m/s。模型sm8的基本参数和sm7相同，关于sm7的基本参数可参见文献[9]。试验中每个波长进行一次拖车，一次拖车中采用两个喷气流量，一个为饱和流量，一个为零流量。试验中对首部、中部和尾部的运动响应进行了测量。对测量的数据采用FFT-FS方法进行了分析，得到各运动响应在遭遇频率附近频段的细化幅值谱，并统计了遭遇频率处的幅频参数。图6给出了波长9 m时重心处的垂荡时历曲线。图7给出了两个垂荡响应信号在遭遇频率附近频段的FFT-FS细化谱及FFT频幅曲线。分析图7的两条细化幅值谱在遭遇频率处的幅值可以发现，喷气时的幅值要小于喷气后的幅值，这和事实是相符的，因为在长波激励时，船模和波浪之间能形成较为稳定的气泡层，气泡层的存在可以缓冲船舶的运动，所以喷气后的船模对波浪的垂荡响应会得到改善，但对比喷气前后的FFT幅值谱在遭遇频率处的幅值可知两者相当接近，说明该方法无法识别气泡层存在给运动响应带来的影响。

图6 实测垂荡响应信号的时历过程Fig.6 History curve of the heave

图7 垂荡响应的FFT、FFT-FS幅值谱比较Fig.7 Amplitude-frequency curves of the signals in evaluated by FFT and FFT-FS

表3 喷气前后FFT-FS、FFT分析所得遭遇频率、幅值统计Tab.3 The encounter frequency and its corresponding amplitude calculated by FFT and FFT-FS

5 结 论

（1）当采样数据较少且频率分辨率较高时FFT-FS运算效率要明显高于FFT的运算效率；

（2）FFT-FS算法分析精度受信噪比的影响很小，是一种适应性广的算法，即使是对强噪声背景下的测量信号进行分析也能确保精度；

（3）当频段半宽为1时谱线数选择50对实测信号进行FFT-FS分析既能保证精度又能确保运算效率；

（4）该算法能有效用在船模耐波性试验测量数据的定量分析中。

[1]彭英声.舰船耐波性基础[M].北京:国防工业出版社,1988:2-14.Pend Y S.Basic theories of ship’s seakeeping[M].Beijing:Publishing House of National Defense Industry,1988:2-14.

[2]赵 霞,熊小伏,郭 珂.用细化频谱技术分析断路器操动机构振动信号[J].电力系统自动化,2003,12(27):37-41.Zhao X,Xiong X F,Guo K.Application of zoom spectrum analysis to circuit breaker operating mechanism vibration[J].Electric Power Systems,2003,12(27):37-41.

[3]程佩青.数字信号处理教程[M].北京:清华大学出版社,2001:144-146.Cheng P Q.A Course in digital signal processing[M].Beijing:Tsinghua University Press,2001:144-146.

[4]王兰炜,赵家骝,王子影.频率细化技术在超低频/极低频电磁信号检测中的应用[J].地震学报,2007,26(1):59-66.Wang L W,Zhao J L,Wang Z Y.Application of zoom FFT technique to detecting EM signal of SLF/ELF[J].ACTA SEISMOLOGICA SINICA,2007,26(1):59-66.

[5]Cheng Junsheng,Yu Dejie,Yang Yu.A fault diagnosis approach for roller bearings based on EMD method and AR model[J].Mechanical Systems and Signal Processing,2006,20:350-362.

[6]何宏斌,席泽敏,刘峰等.基于FPGA的高斯噪声实时产生方法[J].舰船电子工程,2008,6(28):124-125.He H B,Xi Z M,Liu F.Real time Gauss noise generate method based on FPGA[J].Ship Electronic Engineering,2008,6(28):124-125.

[7]Mircea Grigoriu.Control of time delay linear systems with Gaussian white noise[J].Probabilistic Engineering Mechanics,1997,12(2):89-96.

[8]南利平.通信原理简明教程[M].北京:清华大学出版社,2000:43-44.Nan L P.A Concise course of communication principle[M].Beijing:Tsinghua University press,2000:43-44.

[9]Dong W C,Liu Z H.Experimental study on the hull form of high-speed air cavity craft[J].The Ninth International Conference on Fast Sea Transportation,2007:264-269.

[10]许 勇,欧勇鹏,董文才.基于低通滤波和经验模态分解的舰船耐波性试验信号分析方法研究[J].船舶力学,2009,26(1):59-66.Xu Y,Ou Y P,Dong W C.Study on the measured signal analysis method based on low-pass filtering and EMD for ship seakeeping test[J].Journal of Ship Mechanics,2009,5(13):712-717.