复合材料螺旋桨流固耦合分析方法研究

曾志波，姚志崇，王玮波，刘润闻，韩用波，洪方文

（中国船舶科学研究中心，江苏 无锡 214082）

1 引 言

先进复合材料于20世纪60年代问世。复合材料在航空、航天结构上的应用带来了突出的减重效果和综合性能的显著提高，使其成为军用飞机四大结构材料之一[1]。在船舶方面，自20世纪80年代以来，复合材料在水面舰船和水下潜艇方面的应用开始并迅速增长，在舰艇上层建筑、天线系统、螺旋桨、桨轴、舵、泵、管道及机座等方面得到了大范围的应用[2]。

尽管复合材料螺旋桨在商用和军用船艇上得到了相当应用，然而由于缺乏设计方法、系统的经验数据库和可靠的计算工具，大多数螺旋桨仍然完全套用了金属螺旋桨的设计与计算方法。最早的复合材料螺旋桨数值计算技术出现于1991年，Lin等[3-4]采用涡格法（VLM）计算水下无空泡螺旋桨的定常水动力性能，提取桨叶外载荷后，采用有限元（FEM）进行了桨叶应力和变形分析；1994年，Kane和Dow[5]也进行了类似的计算，结果表明:与传统金属桨相比，复合材料螺旋桨具有5～10倍的叶梢变形，但是以上计算结果和实船试航相差较大[2]。在早期的计算中，并未进行流固耦合迭代，因而没有涉及流体、结构的相互作用。1996年，Lin等[6]发展了考虑流固耦合的3D FEM/VLM方法，并用于螺旋桨水动力性能分析，随后，Lin等进一步完善计算方法，2005年增加了应力评估和疲劳标准[7]。Young等[8]和Chen等[9]于2006年进行了复合材料螺旋桨设计与分析，在他们的研究中较全面地考虑流固耦合特性以及非均匀伴流的影响。Young等[10-11]采用面元法和有限元法开展了复合材料螺旋桨流固耦合特性数值计算分析,并与试验结果做了比较，取得了较好的精度。近两年来，Motley等[12-13]采用流固耦合方法针对复合材料节能性能做了分析研究。与国际水平相比，我国的复合材料螺旋桨研究属起步阶段，研究水平停留在小型螺旋桨的单方面的性能或者复合材料的性能上[14-15]。

本文基于面元法和有限元法，采取流固耦合中的弱耦合方法，开展了复合材料螺旋桨流固耦合分析方法研究。首先探讨了复合材料桨叶有限元建模以及水动力外载荷和结构变形的流固耦合交界面数据传递问题；然后在此基础上集成为一项复合材料螺旋桨分析技术，测试了其收敛性；最后进行了比较计算验证，为复合材料螺旋桨性能分析提供了必要的工具。

2 复合材料螺旋桨流固耦合数值分析

本文基于流固耦合中的弱耦合处理方法进行复合材料螺旋桨力学性能分析,其中弱耦合方法的基本思路是在每个时间步内依次对流体力学方程和结构力学方程求解，通过耦合交界面交换固体域和流体域的计算结果数据，反复交替计算从而实现耦合求解，该方法是研究气固耦合（气动弹性）问题的主流方法[16]。在弱耦合数值计算中，采用面元法进行流体域求解，采用有限元法进行固体域求解。对于复合材料螺旋桨的弱耦合分析流程包括:

1）每一时间步对桨叶水动力载荷的面元法计算；

2）水动力载荷向交界面中有限元计算网格的传递；

3）每一时间步对复合材料桨叶位移（变形）等信息的有限元计算；

4）位移（变形）等信息向交界面中面元法计算网格的传递。

本文采用文献[17]中的螺旋桨面元法和文献[18-19]建立的螺旋桨结构力学有限元分析方法建立复合材料螺旋桨弱耦合分析方法。

2.1 复合材料螺旋桨有限元模型与铺层

在ANSYS结构有限元分析中，选取8节点三维层状结构实体单元SOLID46对复合材料桨叶进行网格划分，复合材料螺旋桨有限元模型如图1所示。

螺旋桨采用正交各项异性碳纤维复合材料，材料铺层结构如图2所示，左图显示的铺层分布是[30/-30/90/-90/30]s对称形式，右图为根部铺层结构放大图，共10层，各层之间是等厚度堆栈而成。

图1 复合材料螺旋桨有限元模型Fig.1 The FE model of composite propellers

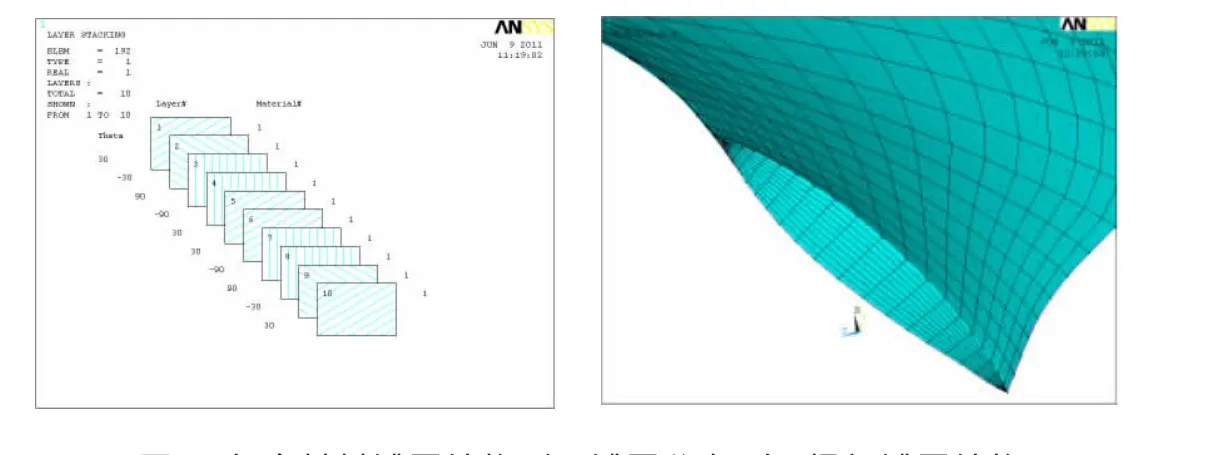
图2 复合材料铺层结构（左:铺层分布；右:根部铺层结构）Fig.2 The layer structure of composite materials(Left:Layer distribution;right:Layer structure in the root)

2.2 复合材料螺旋桨水动力外载荷传递

面元法计算外载荷分布结果通常采取压力分布表示，如图3所示，其中压力系数CP定义如下:

式中:P、P0、ρ和 V 分别为桨叶表面压力（Pa）、参考压力（Pa）、水密度（kg/m3）和桨前方来流水速（m/s）。

采取插值的方式将面元法计算的水动力外载荷从面元法网格传递到有限元计算网格节点上。由于ANSYS复合材料结构分析模块中有限元外载荷由各节点的节点力构成，如图4所示，其中根部施加固定约束。因此，本文先在桨叶面元网格中由压力分布结合各面元的面积和法向矢量计算各面元上的三维作用力，然后进行三维作用力的传递。

任一面元（图5所示面元ABCD）法向方向的作用力计算公式如下:

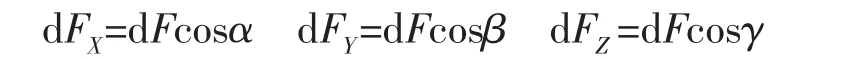
上式中，cosα，cosβ，cosγ为方向余弦，采用螺旋桨面元法中的双曲面元方向[17]。

图3 面元法计算压力分布Fig.3 Pressure distribution from PM

图4 有限元节点力分布Fig.4 Force distribution for FEM

图5 面元ABCDFig.5 A panel ABCD

将计算的各面元三维作用力（图6所示）根据面元网格节点和有限元网格节点之间的位置关系（最小距离原则）传递到有限元网格节点上（图4所示），其中叶背和叶面分别独立进行。传递的三维节点力作为有限元计算边界条件。

图6 计算节点力分布（左:X方向力；中:Y方向力；右:Z方向力）Fig.6 The distribution of calculated forces(Left:X direction;middle:Y direction;right:Z direction)

2.3 复合材料螺旋桨几何变形位移传递

在流固耦合分析中变形后的桨叶需重新进行外载荷计算，因此有限元中计算的复合材料桨叶各节点三向位移需传递给面元网格。本文采用如下插值方法[20-22]:

对于三维桨叶网格坐标（X，Y，Z），其中:X为轴向方向，向后为正，Y为桨叶参考线方向，向上为正，首先将桨叶投影到（X’,Y）平面，其中X’和X轴夹角选取0.7R半径螺距角，如图7所示，使得位移插值量的空间分布在（X’,Y）平面变得平坦，从而提高插值精度；然后在（X’,Y）平面中进行有限元网格点F向目标面元网格点P位移量的插值工作，步骤如下:

1） 在（X’，Y）平面中选出离目标P点最近的15个有限元网格源点Fi）（i=1，2…，15），如图8所示；

2）对于源点 Fi）和位移量 Di（i=1，2…，15）进行二元三次多项式拟合，采用最小二乘法求得三次多项式系数ai（i=1，2…，10），得到拟合公式如下:

4）依次进行面元网格点的插值。

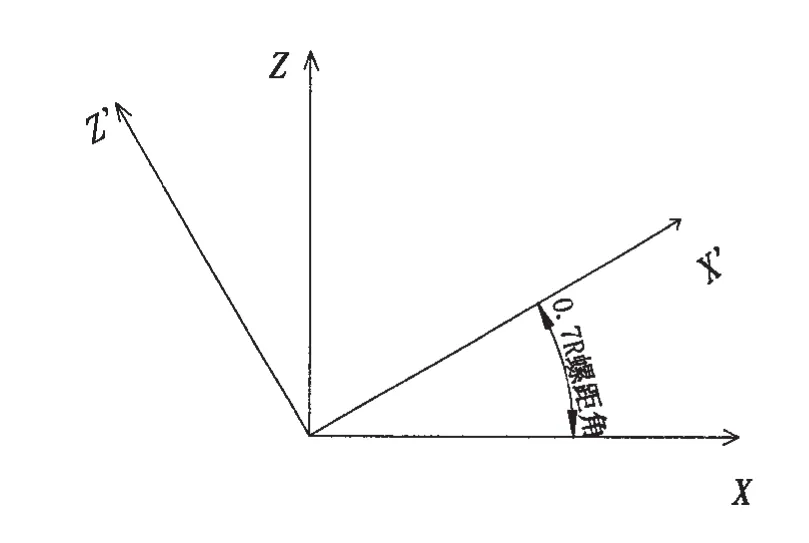
图7 原坐标（X）与投影坐标（X’）Fig.7 Original coodinate(X)and projective coodiante(X’)

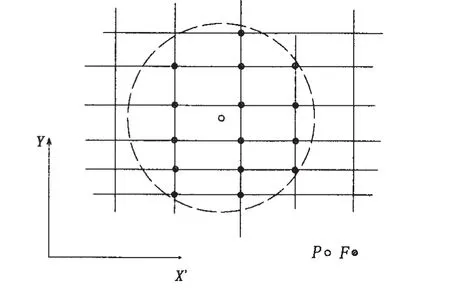
图8 插值点（P）与源点（F）Fig.8 Interpolated point(P)and source points(F)

图9为变形量插值前后的比较，其中左图是有限元计算的总变形量分布，右图是插值到面元法网格上的总变形量；从比较图可以看出，变形量实现了很好的传递。

图9 变形量插值前后比较（左图:插值前，单位m；右图:插值后，单位mm）Fig.9 The comparison of deformation(Left:Before interplolation,m;right:After interplolation,mm)

2.4 复合材料螺旋桨参数反解

由于桨叶形状复杂，为了避免新桨叶面元网格产生畸变现象[22]，面元网格有时必须针对新的桨叶几何进行重新划分；另一方面，复合材料桨叶经过流固耦合作用后，需从变形后的桨叶模型中提取螺距、拱度等特征参数进行分析。以上两个方面需要开展桨叶模型的参数反解工作。

桨叶参数反解按以下两个步骤进行:首先从桨叶三维模型中提取各半径剖面叶背和叶面的三维坐标，可在UG建模软件中实现；然后由各剖面的三维坐标计算桨叶参数，求解螺距、弦长、厚度、侧斜和拱度等构成新桨叶参数型值表。根据以上步骤反解的桨叶参数可达到较高的精度，如图10所示，采用反解的参数建模与原模型的比较，结果十分吻合。

图10 反解桨叶模型与原桨叶模型比较Fig.10 The comparison between reversely extracted blade model and original blade model

2.5 复合材料螺旋桨流固耦合分析集成

2.5.1 分析流程

复合材料螺旋桨流固耦合分析流程如下:

1）对给定的复合材料螺旋桨几何型值，采用UG建模，并输入到ANSYS有限元分析软件，进行网格划分；

2）对给定运行工况，采用面元法进行桨叶网格划分，进而离散面元法方程，求解桨叶表面压力分布，计算各面元三维作用力；

3）将面元三维作用力传递到（1）中有限元划分的网格节点上，进行复合材料属性及铺层结构设置，对结构力学分析方程进行有限元求解，得到桨叶位移。

4）将有限元计算的各网格点位移插值到原始桨叶面元法中的面元网格节点上，得到变形后的桨叶几何，提取新的桨叶几何型值；

5）判断新的桨叶几何是否收敛，如果收敛，则结束；如果不收敛，则将新的桨叶几何带回（2），进行（2）～（5）的迭代计算，直至收敛。

上述分析流程见图11。

2.5.2 收敛性

螺旋桨根据侧斜方向不同可分为前侧斜螺旋桨和后侧斜螺旋桨，图12给出了从桨后向桨前方向看的两种侧斜分布螺旋桨桨叶模型。目前，船舶螺旋桨大多采用后侧斜螺旋桨，对于前侧斜螺旋桨也有学者研究其对梢涡空泡起始性能的影响[23]。

复合材料螺旋桨采取不同的侧斜分布，呈现不同的流固耦合收敛过程，如图13所示。图13左图表示后侧斜复合材料螺旋桨的收敛过程，图中螺旋桨推力系数和扭矩系数以及0.7R螺距比呈现交替收敛形式，最终收敛桨叶螺距变小，相应的载荷变小。而对于前侧斜复合材料螺旋桨的收敛过程，呈现单调收敛过程，如图13右图所示，最终收敛桨叶螺距变大，相应的载荷变大。

图11 复合材料螺旋桨流固耦合分析流程Fig.11 The flow chart of FSI analysis for composite propellers

图12 不同侧斜螺旋桨（左:后侧斜；右:前侧斜）Fig.12 Different skewed propellers(Left:Backward skew;right:Forward skew)

图13 复合材料螺旋桨流固耦合收敛过程（左:后侧斜；右:前侧斜）Fig.13 The convergence process of FSI of composite propellers

3 复合材料螺旋桨流固耦合分析方法比较验证

采取本文建立的流固耦合分析技术，针对文献[12]中5474桨进行了比较计算验证。在比较计算中采用相同的Hexcel IM7-8552碳纤维复合材料、铺层方式，材料属性如表1所示。

表1 Hexcel IM7-8552碳纤维复合材料属性Tab.1 Material properties of Hexcel IM7-8552

图14给出了复合材料螺旋桨变形前后面元法计算的推力系数和扭矩系数，其中流固耦合迭代计算点:进速系数为J=0.66，转速n=780 rpm。在图14中也给出了文献[12]的计算结果，本文计算的推力系数和扭矩系数与文献[12]结果的差别在4%以内。图15为变形前后的螺距角分布比较，变形后从根部到梢部螺距角变形量逐渐增大，变形后梢部螺距角计算结果与图中文献[12]计算结果吻合良好。

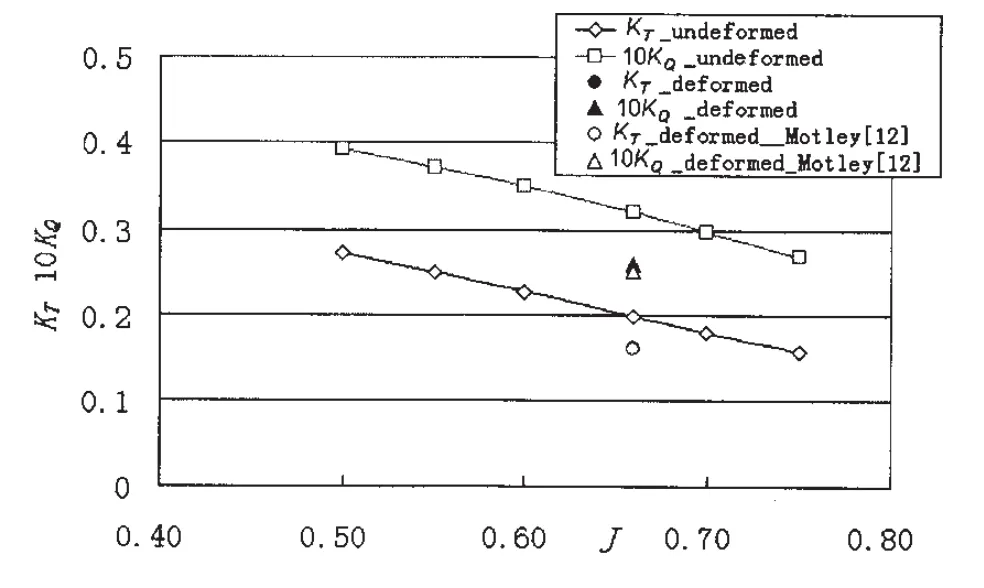
图14 5474复合材料螺旋桨水动力比较Fig.14 The comparison of hydrodynamic performance of composite propeller 5474

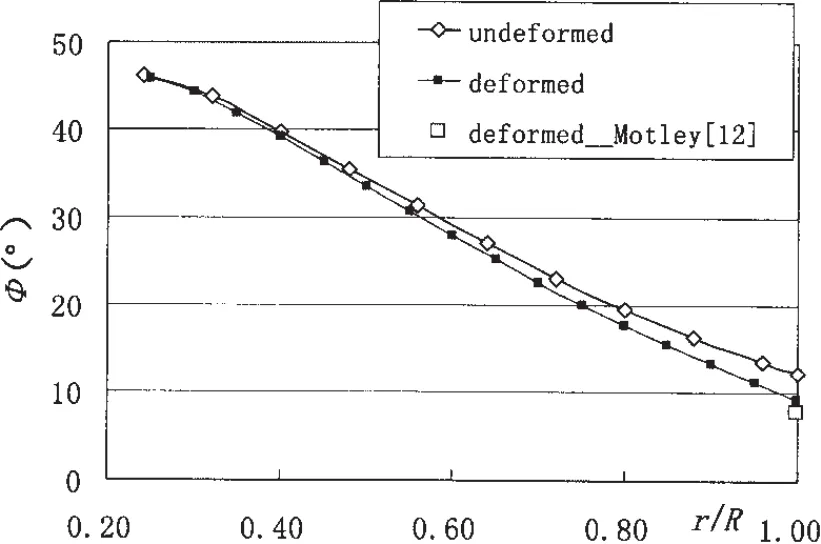
图15 5474复合材料螺旋桨螺距角分布比较Fig.15 The comparison of pitch angle distribution of composite propeller 5474

4 结 论

本文研究了复合材料螺旋桨流固耦合（弱耦合）分析方法。重点探讨了复合材料桨叶有限元建模以及流固耦合中载荷及几何变形量的传递问题，采用的方法对复合材料螺旋桨具有较好的适用性。集成的复合材料螺旋桨流固耦合分析技术对不同侧斜螺旋桨进行的迭代计算均可获得收敛解，针对5474复合材料螺旋桨的计算结果与文献的吻合较好。后续的工作是开展复合材料螺旋桨性能研究，剖析复合材料螺旋桨流固耦合变形规律。

[1]杨乃宾,章怡宁.复合材料飞机结构设计[M].北京:航空工业出版社,2004.

[2]Mouritz A P,Gellert E.Review of advanced composite structures for naval ships and submarines[J].Composites Structures,2001,53:21-41.

[3]Lin G.Comparative stress-deflection analyses of a thick-shell composite propeller blade[R].David Taylor Research Center,DTRC/SHD-1373-01,1991a.

[4]Lin G.Three-dimensional stress analyses of a fiber-reinforced composite thruster blade[C]//Symposium on Propellers/Shafting Society of Naval Architects and Marine Engineers.Virginia Beach,VA,USA,1991b.

[5]Kane C,Dow R.Marine propulsors design in fibre reinforced plastics[J].J Defence Sci,1994,4:301-308.

[6]Lin H,Lin J.Nonlinear hydroelastic behavior of propellers using a finite element method and lifting surface theory[J].Journal of Marine Science and Technology,1996,1(2):114-124.

[7]Lin H,Lin J.Strength evaluations of a composite marine propeller blade[J].Journal of Reinforced Plastics and Composites,2005,17:1791-1807.

[8]Young Y L,Michael T J,Seaver M,Trickey S T.Numerical and experimental investigations of composite marine propellers[C]//26th Symposium on Naval Hydrodynamics.Rome,Italy,2006.

[9]BenjaminY-H Chen,Stephen K Neely,et al.Design,fabrication and testing of pitching-adapting(flexible)composite propellers[C].The SNAME,Propellers/Shafting Symposium,2006.

[10]Young Y L.Time-dependent hydroelastic analysis of cavitating propulsors[J].Journal of Fluids and Structures,2007,23(2):269-295.

[11]Young Y L.Fluid-structure interaction analysis of flexible composite marine propellers[J].Journal of Fluids and Structures,2008,24:799-818.

[12]Motley M R,Liu Z,Young Y L.Utilizing fluid structure interactions to improve energy efficiency of composite marine propellers in spatially varying wake[J].Composite Structures,2009,90(3):304-313.

[13]Motley M R,Young Y L.Performance-based design of adaptive composite marine propellers[C]//28th Symposium on Naval Hydrodynamics.Pasadena,California,USA,2010.

[14]杨传勇.小型船舶复合材料船用螺旋桨的设计与分析[D].大连:大连海事大学,2005.

[15]洪 毅.复合材料船用螺旋桨结构设计研究[D].哈尔滨:哈尔滨工业大学,2006.

[16]叶正寅,张伟伟,史爱明等.流固耦合力学基础及其应用[M].哈尔滨:哈尔滨工业大学出版社,2010.

[17]董世汤,唐登海,周伟新.CSSRC的螺旋桨定常面元法[J].船舶力学,2005,9(5):48-62.Dong Shitang,Tang Denghai,Zhou Weixin.Panel method of CSSRC for propeller in steady flows[J].Journal of Ship Mechanics,2005,9(5):46-60.

[18]姚志崇,洪方文,丁恩宝.基于work bench的螺旋桨流固耦强度校核数值模拟[C].2007ANSYS-CFD年会文集,2007.

[19]姚志崇,曾志波.复合材料船用螺旋桨流固耦合性能分析[C].2010全国固体力学大会,华中科技大学,2010.

[20]李立州,王婧超,吕震宙,岳珠峰.学科间载荷参数空间传递方法[J].航空动力学报,2007(07):32-36.

[21]虞跨海,岳珠峰.涡轮冷却叶片参数化建模及多学科设计优化[J].航空动力学报,2007(08):144-149.

[22]岳珠峰等.航空发动机涡轮叶片多学科设计优化[M].北京:科学出版社,2007.

[23]Kuiper G,Van Terwisga T J C,Zondervan G J,Jessup S D,Krikke E M.Cavitation inception tests on a systematic series of two-bladed propellers[C]//26th Symposium on Naval Hydrodynamics.Rome,Italy,2006.