关于动力学曲线初始点切线的讨论
靳福全
(太原工业学院化学与化工系 山西太原 030008)
动力学是物理化学的重要组成部分,研究动力学就是研究反应机理、反应速率及其影响因素。其中动力学方程的确定是动力学部分的一个主要内容。为了避开逆反应的影响,常用初始浓度法确定动力学方程中的反应级数和速率常数。本文以一般的对行反应、平行反应及连串反应作为研究对象,应用数学方法导出了指定反应物和指定产物的动力学曲线初始点的切线方程,并给出了指定反应物动力学曲线初始点切线在横轴上的截距表达式和指定产物动力学曲线初始点切线在y=cA,0水平线上的截距表达式;重点对指定反应物和指定产物系数相等时的情况作了具体分析,得出了一些有意义的结论。提出了一种确定动力学方程中反应级数和速率常数的方法——初始浓度截距法。
1 对行反应[1]
对于开始时,只有反应物而无产物的对行反应
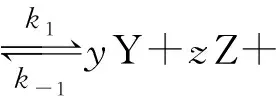
反应物A的净消耗速率为:
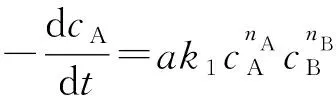
由导数意义知,cA-t曲线在初始点(0,cA,0)的切线斜率为:

过初始点(0,cA,0)的切线(记为a1)方程为:
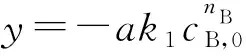
切线a1在横轴上的截距为:
产物Z的净生成速率为:
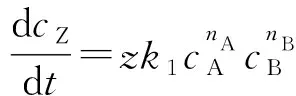
由导数意义知,cZ-t曲线在初始点(0,cZ,0)亦即(0,0)的切线斜率为:
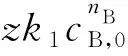
过初始点(0,cZ,0)亦即(0,0)的切线(记为b1)方程为:

切线b1在y=cA,0水平线上的截距为:

2 平行反应
对于开始时,只有反应物而无产物的平行反应
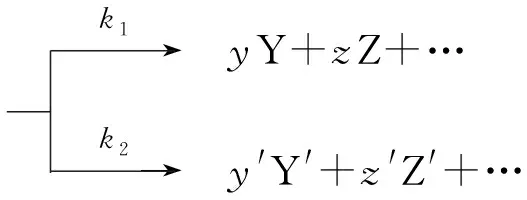
反应物A的总消耗速率为:
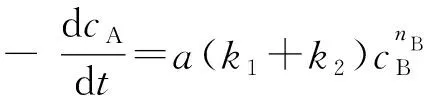
由导数意义知,cA-t曲线在初始点(0,cA,0)的切线斜率为:
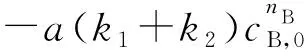
过初始点(0,cA,0)的切线(记为a2)方程为:
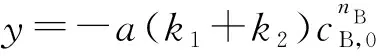
切线a2在横轴上的截距为:
产物Z的生成速率为:
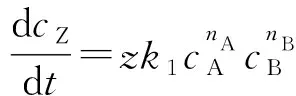
由导数意义知,cZ-t曲线在初始点(0,cZ,0)亦即(0,0)的切线斜率为:
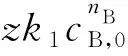
过初始点(0,cZ,0)亦即(0,0)的切线(记为b2)方程为:

切线b2在y=cA,0水平线上的截距为:
产物Z′的生成速率为:
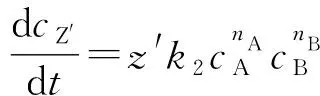
由导数意义知,cZ′-t曲线在初始点(0,cZ′,0)亦即(0,0)的切线斜率为:

过初始点(0,cZ′,0)亦即(0,0)的切线(记为c2)方程为:
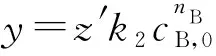
切线c2在y=cA,0水平线上的截距为:
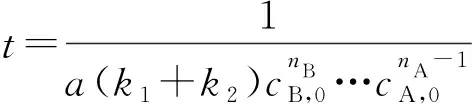
3 连串反应
对于开始时,只有反应物而无产物的连串反应

反应物A的消耗速率为:
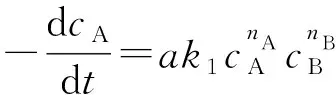
由导数意义知,cA-t曲线在初始点(0,cA,0)的切线斜率为:

过初始点(0,cA,0)的切线(记为a3)方程为:
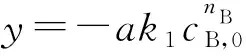
切线a3在横轴上的截距为:
中间产物Z的净生成速率为:
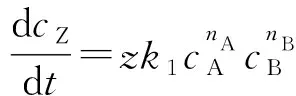
由导数意义知,cZ-t曲线在初始点(0,cZ,0)亦即(0,0)的切线斜率为:
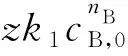
过初始点(0,cZ,0)亦即(0,0)的切线(记为b3)方程为:

切线b3在y=cA,0水平线上的截距为:
产物Z′的生成速率为:
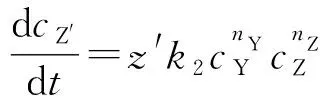
由导数意义知,cZ′-t曲线在初始点(0,cZ′,0)亦即(0,0)的切线斜率为0;过初始点(0,cZ′,0)亦即(0,0)的切线(记为c3)方程为:
y=0

4 应用
从前面推出的各类反应的初始点切线的截距与初始浓度关系式可看出:若截距与初始浓度无关,则为一级反应;若截距与初始浓度有关,则为非一级反应。文中导出的结论对对行反应、平行反应及连串反应动力学曲线的绘制具有一定指导意义,可用其来分析动力学曲线初始段变化趋势是否合理。
利用前面导出的初始点切线斜率和初始浓度的关系式或初始点切线在横轴上的截距和初始浓度的关系式,可确定反应级数和反应速率常数。下面以对行反应为例,说明应用上述两种关系式确定反应级数和速率常数的方法。
4.1 初始浓度斜率法
4.2 初始浓度截距法
参 考 文 献
[1] 刘俊吉,周亚平,李松林.物理化学(下册).第5版.北京:高等教育出版社,2009

