关于熵判据、亥姆霍兹函数判据和吉布斯函数判据的讨论

王新平 王旭珍 王新葵 李醒龙 蒋晨然 任延煜

(大连理工大学化工与环境生命学部化学学院 辽宁大连 116024)

1问题的提出

无需环境做功，就可以发生的不可逆过程称为自发性过程[1-3]。通过物理化学的学习，使学生能正确地判断过程的自发性是很重要的，因为这是利用自发趋势较大的过程生产目的产物和开发新能源，以及通过向系统输入功的办法使非自发过程实际进行的基础。在物理化学学习中，能力较强的学生为了使自己所学的相应知识更加深入清晰，经常拿出不同物理化学参考书中的相关问题，让教师答疑。本文提出的命题即来源于学生的下述问题：

“用由熵增原理得到的公式

ΔS隔离=ΔS系统+ΔS环境

判断过程的自发性时，允许系统和环境之间有热量交换，那么是否也允许它们之间有功的交换？”。

这是一个很难回答的问题，因为它涉及到原命题的正确性。笔者认为，这样不太清晰的认识，可能会在一些大学的学生中普遍出现。为了更好地进行物理化学教学，值得在同行中对这个问题进行深入讨论。

2 结果和讨论

2.1 熵判据

首先必须强调的是，熵增原理，即所谓熵判据，并不能用于判断过程的自发性。为便于对此确认，在这里先给出得到熵增原理的关键推导脉络:

将卡诺定理推广到有多个热源、使用理想气体为工质、每个无限小的过程都是卡诺循环中的可逆膨胀或可逆压缩的情况时为:

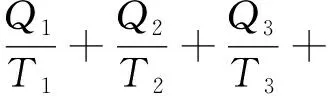
该循环过程表示为:

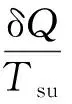
对于绝热系统，可以推导得到:

ΔS绝热(A→B)≥0 (>0，不可逆；=0，可逆)

这就是熵增原理。由上述熵增原理的推导过程，能够得到以下两点结论。

1) 一个不可逆过程可能是自发过程，也可能是非自发过程。所以，用熵增原理只能判断绝热条件下过程的可逆性，而不能判断绝热条件下过程的自发性。

2) 在熵增原理得出的推导过程中，并未涉及非体积功。因此，熵增原理应表述为：在绝热和无非体积功的条件下，可逆过程会维持系统的熵不变；绝热条件下的所有不可逆过程都是增熵过程，使系统的熵值变小的过程，是不可能实现的(即不能实际发生)。

下面的例题对于正确理解熵增原理很有帮助。

例题1:将物质的量为n，温度为T1，体积为V1的理想气体，在绝热条件下压缩到体积为V2。求在下列两种压缩方式条件下系统的熵变。

1) 以准静态方式进行。

2) 用任意不可逆方式进行。

解:由热力学第一定律，环境在绝热条件下将系统压缩时所付出的功全部转化为系统的热力学能。即理想气体的温度一定升高，而其最终温度与环境所付出功的大小直接相关。

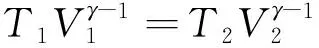
由理想气体的熵变计算公式

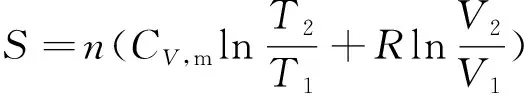
(1)

可得ΔS=0。

不可逆方式可以多种多样，环境所付出功的大小不尽相同，相应使得熵变的大小也不同，但ΔS>0永远成立。

环境做功将绝热筒中的气体(视为系统)压缩，是一个典型的非自发过程。但是，它却满足ΔS绝热(A→B)≥0的条件。这充分表明，熵增原理不能成为过程自发性的判据。但是，例题1这一典型实例，则支持熵增原理对于过程能否实际发生，以及以什么方式(可逆或不可逆)进行的判据。

上述例题表明，熵增原理并不排斥环境对系统做体积功的情况。

前述学生的问题，则是将熵增原理推广到由实际系统和实际环境构成的虚拟系统，以便更广泛地应用熵增原理的情况。

由于虚拟的隔离系统满足绝热条件,因此有：

ΔS隔离=(ΔS系统+ΔS环境)≥0 (>0，不可逆；=0，可逆)

(2)

显然，在该虚拟的隔离系统内部，实际系统和实际环境之间热和功的交换并不排斥式(2)的成立。也就是说，对于所研究的实际系统，无论它和环境之间热和功的交换如何，只能实现(ΔS系统+ΔS环境)≥0的过程。能够以不可逆方式实现的过程对应(ΔS系统+ΔS环境)>0；能够以可逆方式实现的过程，其(ΔS系统+ΔS环境)=0。例题2则有助于深刻理解这一点。

例题2:抽出插板，让与环境有良好接触的温度均为T、体积均为V1、物质的量分别为n1和4n1的O2和N2(可视为理想气体)定温混合(过程Ⅰ)，再将混合气体定温压缩为V1(过程Ⅱ)(图1)。① 用热力学第二定律验证过程Ⅰ的不可逆性。② 让过程Ⅱ分别以不可逆和可逆的方式进行，验证热力学第二定律对过程可逆性判断的正确性。

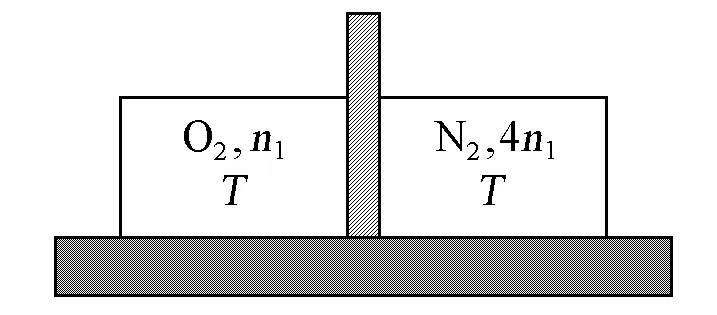
图1 示意图

解:

① 过程Ⅰ:

ΔSsy(Ⅰ)=ΔS(O2)+ΔS(N2)=5n1Rln2

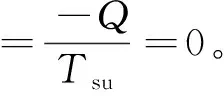
ΔS孤立(Ⅰ)=ΔS(Ⅰ)+ΔSsu(Ⅰ)= 5n1Rln2>0

则该气体定温混合过程为不可逆过程。

虽然系统的熵变为ΔSsy(Ⅱ)=-5n1Rln2，但环境的熵变依压缩方式不同而不同。

该压缩过程为理想气体定温过程，则ΔU=0，而Qsu=-Q=W。

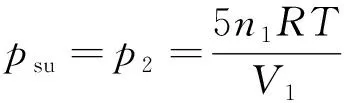
则：

ΔS孤立(Ⅱ)=ΔSsy(Ⅱ)+ΔSsu(Ⅱ)=5n1R(1-ln2)>0

所以，用热力学第二定律可判断该压缩过程为不可逆过程。

2) 以环境的压力始终极接近系统的压力psu=p+dp≈p对系统加压压缩：

则:

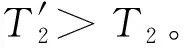
ΔS孤立′ (Ⅱ)=ΔS(Ⅱ)+ΔSsu′(Ⅱ)≈-5n1Rln2+5n1Rln2=0

在例题2中，过程Ⅰ和过程Ⅱ以不可逆方式进行时，虽然它们均对应ΔS孤立(Ⅱ)=ΔSsy(Ⅱ)+ΔSsu(Ⅱ)>0，但前者是自发的不可逆过程，而后者却是非自发的不可逆过程。这再次证明，用热力学第二定律只能判断过程进行的可逆性，而不能判断过程的自发性。即(ΔS系统+ΔS环境)>0只能说明系统进行的过程能够以不可逆方式实现。至于它是否自发发生，则无从判断(无论从熵增原理的推导过程看还是从上述例题看，用热力学第二定律判断过程的自发性都是错误的)。该例题还表明，当系统和环境有功交换时，依据熵增原理仍能对过程的可逆性给出正确的判断。

2.2 亥姆霍茨函数判据

亥姆霍茨函数判据，能够用于判断定温、定容条件下过程的自发性。这可由以下推导过程得到确认。

由热力学第二定律：

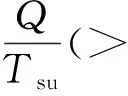
即：

Tsu(S2-S1)≥Q

在定温条件下，T2=T1=Tsu,则:

T2S2-T1S1≥Q

又:

Q=ΔU-W

于是有：

-((U2-T2S2)-(U1-T2S1))≥-W

(3)

即：

-ΔAT≥-W(>，不可逆；=，可逆)

如过程不仅定温而且定容，则体积功WV=0,于是有：

-ΔAT，V≥-W′(>，不可逆；=，可逆)

(4)

若非体积功W′为0，则过程的功W=0。这就是说，此时系统和环境间完全没有功的传递，此时的不可逆过程，就是严格意义上的自发过程。因此，式(4)变为:

ΔAT，V≤0(<0，自发；=0，可逆)

(5)

这就是亥姆霍茨函数判据。

由以上亥姆霍茨函数判据的导出过程可以看出，用它来判断过程的自发性才是科学的。在定温、定容、W′=0的条件下，ΔAT，V<0的过程自发地进行；而ΔAT，V=0的过程，实际则处于平衡状态。依据状态函数的性质，在定温、定容且W′=0的条件下，一个ΔAT，V>0的过程，其逆向过程一定为ΔAT，V<0。因此，ΔAT，V>0的过程是非自发的，即其逆向过程自发地进行。

这里必须强调的是，亥姆霍茨函数判据的应用不应仅仅限于对过程自发性的判断，而更应在于其下述应用：

1) 判断利用自发过程，在定温、定容条件下环境可获取的最大非体积功。

对于一个定容条件下的自发过程(其ΔAT，V<0)，由式(4)可知，只要满足-ΔAT,V≥-W′，则过程就是可以实现的。即，封闭系统在定温、定容过程中，对环境能做的最大功(自发沿可逆途径进行)等于系统亥姆霍茨函数的减少。该式可为探寻开发获取定容条件下的新能源给出重要的启示。

2) 判断要实现一个定温、定容条件下的非自发过程，环境至少必须付出的非体积功。

将式(4)变为：

ΔAT,V≤W′(<，不可逆；=，可逆)

(6)

式(6)表明，对于一个定容条件下的非自发过程(其ΔAT，V>0)，只要环境为其做非体积功等于或超过系统的亥姆霍茨函数变ΔAT，V，则仍可使该过程可逆或不可逆地实现。虽然在定容条件下的过程不多，但实际生活中并不乏这样的实例。如，给封闭的手机电源充电。

2.3 吉布斯函数判据

用吉布斯函数判据可判断在定温、定压条件下过程的自发性，同样可由其推导过程得到确认。

如过程在定温、定压下进行，有：

W=WV+W′=-psu(V2-V1)+W′=-p2V2+p1V1+W′

则式(3)可写为：

-((U2+p2V2-T2S2)-(U1+p1V1-T1S1))≥-W′

上式即：

-ΔGT,p≥-W′(>，不可逆；=，可逆)

(7)

在定压条件下，系统的体积膨胀或缩小时，虽然涉及定压体积功，但那是维系定压条件的自然结果，不是人为地通过压力差注入的体积功[3]。因此，在定温、定压下，W′=0的不可逆过程即自发过程。于是有：

ΔGT,p≤0(<0，自发；=0，可逆)

(8)

式(8)即为吉布斯函数判据。该判据表明，在定温、定压且W′=0的条件下，如ΔGT,p<0，则过程自发发生；如ΔGT,p>0，则相应过程为非自发过程；如ΔGT,p=0，则系统处于平衡。

同亥姆霍茨函数判据类似，吉布斯函数判据的应用也不应仅仅限于对过程自发性的判断，而更应在于其下述应用：

1) 判断利用自发过程，在定温、定压条件下环境可获取的最大非体积功。

对于一个定压条件下的自发过程(其ΔGT，p<0)，由式(7)可知，只要满足-ΔGT,p≥-W′，则过程就是可以实现的。即，封闭系统在定温、定压过程中，系统对环境能做的最大非体积功(自发沿可逆途径进行)等于系统吉布斯函数的减少。式(8)可为探寻开发获取定压条件下的新能源给出重要的启示。例如，探寻利用新反应的高能燃料电池。它表明，要通过化学反应获取更多的非体积功(如电能)，必须把目光瞄向那些ΔrGm,T,p值为负且其绝对值更大的反应。

2) 判断要实现定温、定压条件下的一个非自发过程，环境至少必须付出的非体积功。

将式(7)变为：

ΔGT,p≤W′(<，不可逆；=，可逆)

(9)

式(9)表明，在定温、定压下，一个非自发过程并非不能实现。只要环境对系统所做的非体积功大于封闭系统中该过程吉布斯函数的改变量，就可以实现。例如水的电解、植物的光合作用等。显然，式(9)对于利用现有能源，开发新的反应途径或新产物给出了重要启示。

3 结论

熵判据、亥姆霍兹函数判据和吉布斯函数判据是化学热力学中很重要的3个判据。准确灵活地应用亥姆霍兹函数判据和吉布斯函数判据判断过程的自发性，目标准确地利用自发反应开发高效新能源，有效地利用现有能源开发非自发过程是化学热力学的重要核心内容。笔者认为，在物理化学教学中，应避免对第一个判据的误用。同时，也应强化后两个判据的外延。这样，才能使相应内容与电化学、光化学内容构成畅通的知识体系，有利于学生掌握贯通的物理化学知识，培养学生创新能力。

参 考 文 献

[1] 胡英，吕瑞东，刘国杰，等. 物理化学.第5版.北京:高等教育出版社，2007

[2] 傅献彩，沈文霞，姚天扬，等.物理化学.第5版.北京:高等教育出版社，2008

[3] 刘俊吉，周亚平，李松林.物理化学.第5版.北京:高等教育出版社，2009