具有Markov转换的Logistic方程的随机持久性和全局吸引性

崔建斌，付桐林

(陇东学院 数学与统计学院， 甘肃 庆阳 745000)

0 引言

文献[1][2]曾讨论了没有Markov转换的非自治的随机Logistic方程

dN(t)=N(t)[a(t)-b(t)N(t)dt+α(t)dB(t)]，t≥0

并给出了依概率全局稳定和随机持久的条件。带有白噪声和Markov转换的Logistic方程：

(1)

其初值条件为X(0)=x和ξ(0)=i∈S，其中ξ(t)为右连续的在有限状态空间S={1，2，…，N}中取值的Markov链，是一维Brown运动。设Markov链ξ(t)是Ft适应的，并且与Brown运动Bt独立。方程(1)可以看成是系统按照Markov链的规律在下面N个方程中由一个到另一个转换：

注意到方程(1)虽然满足局部Logistic条件，但不满足线性增长条件。

1 随机Logistic方程的随机持久性和全局吸引性

令ξi(t)是0时刻由i∈S出发的Markov链。记方程(1)满足初始条件X(0)=x>0，ξ(0)=i∈S的初值解为Xx，i(t)(t≥0)。

令

并假设：

(H1)r(i)>0，K(i)>0，i∈S；

(H2)r*-(σ*)2>0。

定理1：设条件(H1)成立，则方程(1)存在满足初始条件X(0)=x>0，ξ(0)=i∈S的唯一连续正解Xx，i(t)，其表达式为

(2)

证明： 设τ1>0是ξi(t)的第一个跳跃时刻，设在时刻τ1，ξi(t)由状态i转到状态j，设τ2>τ1是第二个转换时刻。不失一般性，只考虑t∈[τ1，τ2)的情况。下面来证明此时有

Xx，i(t)=XXx，t(τ1)，j(t)，t∈[τ1，τ2)

(3)

当t∈[0，τ1]时，由文献[2]中的定理2.2，式(2)成立。于是有

(4)

对t∈[τ1，τ2)，由式(4)得到

=(XXx，i(τ1)，j(t))-1

这就是所需要的结论。

定理2：设条件(H1)和(H2)成立，Xx，i(t)和Xy，i(t)分别是方程(1)满足初始条件X(0)=x>0，ξ(0)=i∈S和X(0)=y>0，ξ(0)=i的解，则有

证明：考虑liapunov函数V(t)=|logXx，i(t)-logXy，i(t)|，t≥0。由推广的Ito公式[3]得到

沿着系统解的正向V(t)的右导数满足

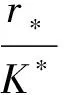
(5)

由式(5)，0到t积分得到

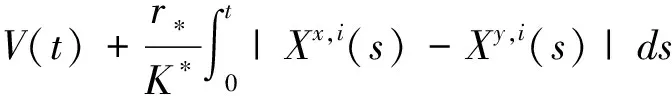
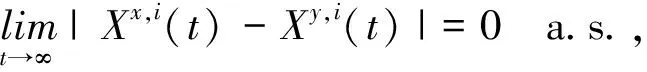
由定理2可以看出方程(1)的解互相吸引，事实上，任意的正解都可以看成是系统的吸引子。

引理3：设条件ξ(t)是右连续的并在有限状态空间S={1，2，…，N}中取值的Markov链，则

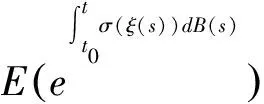
证明：由推广的Ito公式[7，8]得

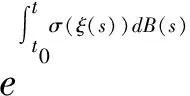
在上式两端取均值有

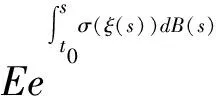
应用Gronwall不等式[4]就得到

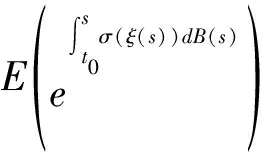
证明完成。

定理4：设条件(H1)和(H2)成立，则具有初始条件X(0)=x>0，ξ(0)=i∈S的解Xx，i(t)有如下性质：

证明：把方程(1)写成积分形式为

两端取均值得到

即

(6)

根据Jensen不等式[5]有

考虑下面的辅助常微分方程：

(7)

方程(7)是一个Logistic方程[6]，其解显然满足

应用比较定理得到

即

两端取均值得到

即

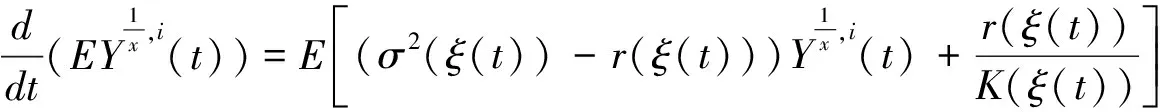
由比较定理[7，8]，得到

根据Jensen不等式有

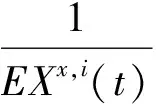
证明完成。

2 结语

在满足线性增长的条件下，我们考虑给出了具有markov转换的随机Logistic方程的解的存在唯一性和解的上、下界，得到了解的随机持久性和全局吸引性。从而推广了以往非线性增长条件下的情形。

[参考文献]

[1] Jiang D Q，Shi N Z，A note on non-autonomous logidtic equation with random perturbation[J].J.Math.Anal.Appl.,2005,303: 164-172

[2] Jiang D Q，Shi N Z，Li X Y,Global stability and stochastic permanence of a non-autonomous logidtic equation with random perturbation[J].J.Math.Anal.Appl.,2006,340: 588-597.

[3] Stevene Shreve.Stochastic Calculus for Finance[M]. New York: Springer,2008:251-269.

[4] IoanniS Karatzas,Steven e Shreve. Methods of Methematical Finnance[M]. New York: SpringerVerlag, 2004:36-69.

[5] Ioannis Karatzas,M.Yor. Martingale Methods in Finnancial Modelling[M]. New York: SpringerVerlag,1998:205-228.

[6] Zhu C,Yin G.On hybrid competitive Lotka-Volterra ecosystems[J].Nonlinear Analysis,2009,71:1370-1379.

[7] Zhu C,Yin G.On competitive Lotka-Volterra model in random environments[J].J.Math.Ana.Appl.,2009, 357:154-170.

[8] Li X,Mao X.Population dynamical behavior of nonautonomous Lotka-Volterra competitive systems with random perturbation[J].Discrete and Continuous Dynamical Systems,2009,24:523-545.