基于离散单元法的滑坡堆积及其涌浪计算

徐 寅 ，陈胜宏

（1.武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2.南昌工程学院 水利与生态工程学院，南昌330029）

1 引 言

边坡分布广泛，对边坡稳定性的研究一直是工程地质和岩土工程界研究的一个难点和热点问题。我国是一个滑坡灾害极为频繁的国家，尤其是随着西部大开发战略的进一步实施，一批大型或特大型的水电工程在我国西南高山峡谷地区兴建，滑坡更是表现出规模大、危害大和机制复杂等特点，在全世界范围内具有典型性和代表性[1]。由于岩体中往往含有断层、节理、裂隙、软弱夹层等大量不同构造、产状和特性的不连续结构面，给岩质边坡的稳定性分析带来了巨大的困难[2]。

目前，研究边坡稳定的方法主要有刚体极限平衡法及有限单元法。刚体极限平衡法以原理简单、有大量的工程经验且有与之相配套的规程规范，在岩土工程中应用较广。有限单元法能考虑真实的应力-应变关系，为准确地模拟边坡的变形破坏提供了强有力的手段。尽管如此，上述两种方法对分析和预测边坡的整个破坏过程还无能为力。然而，给人类带来巨大灾害的往往是大型高速滑坡的失稳。它的失稳会导致岩土体高速入水，不仅会冲毁水工建筑物、航行船只、堵塞河道，而且还会激起巨大的涌浪，威胁库区坝体及沿岸居民生命财产安全[3]。要想分析和预测这类高速滑坡的失事影响范围及处理措施，需要研究滑坡失稳的整个过程。

20世纪70年代初由Cundall[4]提出的离散单元法是一种将弱面所切割的岩体视为复杂的块体的集合体，允许各个块体可以平移或转动，甚至相互分离。离散单元法最初用于模拟岩石边坡的渐进破坏过程，之后经历从二维到三维，从刚性块体到变形块体的发展过程[5]。目前，离散单元法已广泛应用于边坡[6]、地基[7]、地下洞室[8]等的破坏分析。离散单元法的最大特点是能实现边坡从稳定状态到极限平衡状态再到边坡分解、脱离、滑动的过程。因此，采用离散单元法对边坡失稳的整个过程进行研究是可行的且非常有意义的。本文采用离散单元法研究库岸边坡失稳后的滑坡速度并对滑坡体滑入水库中所产生的涌浪进行了评估，并通过离散单元法研究了滑坡的堆积形状，以便对滑坡的灾害进行评估。

2 离散元软件开发

前后处理相对于数值计算来说，虽然是服务性质的，但它们的重要性不言而喻，是数值程序是否完善的一个重要标志，由于离散单元法允许块体与块体可以脱离开来，块体的位置变化可能较大，因此，前后处理器对离散单元法来说显得尤为重要[9]。本文的计算流程如图1所示，图中的“读入数据”和“生成DEM模型”模块相当于前处理部分，“输出结果”模块相当于后处理部分。为了直观地描绘离散元模型及其计算后所得到的块体运动，本文根据图1所给出的流程图并采用VC++与OpenGL相结合的方法，开发了具有前后处理功能的离散单元法软件CORE_DEM。

3 离散单元法的基本原理

离散单元法的实质就是将求解区域离散成有限个完全独立的块体，使求解区域成为一个块体的系统，再对块体之间的接触关系进行判断，以确定块体的受力，最后采用差分方法求解基于牛顿第二定理的块体运动方程。

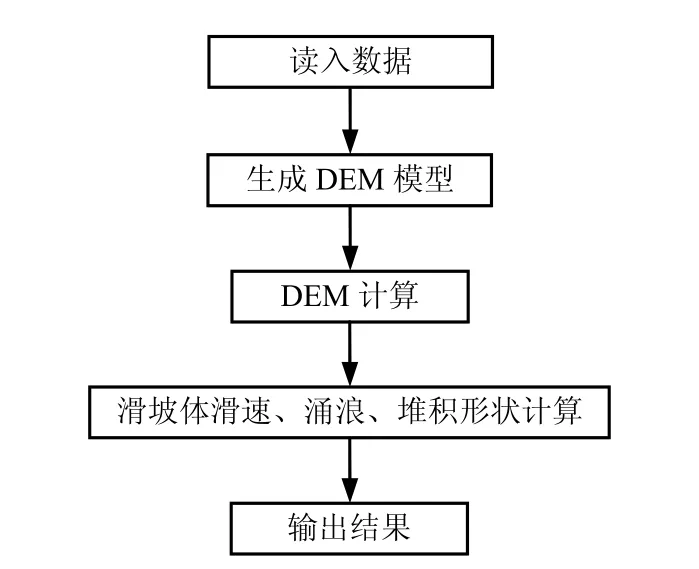
图1 计算流程图Fig.1 Flow chart of calculation

3.1 接触判断

模拟不连续系统破坏过程的复杂力学行为的关键之一是快速有效检测和识别块体的接触关系[10]。一般地，接触判断分两个阶段，即粗判与细判。粗判的目的是排除不可能接触的块体，避免处理没有相互接触的块体的检索，以节省计算时间；细判的目的就是对粗判得到的相关块体进行进一步的接触判断，以提供明确的接触位置和接触法线方向，以便块体之间接触力的确定。

3.2 块体运动

离散单元法采用显式差分方法求解块体运动系统。在每个时间步上，用运动方程和本构方程来描述块体的运动。当把块体视为刚体时，本构方程用接触力与侵入深度间的关系来表示。首先通过对运动方程的积分来更新块体的位置、速度及侵入深度增量；然后通过接触力与侵入深度的关系来确定新的接触力，在新接触力的基础上开始下一步的循环。计算循环见图2。

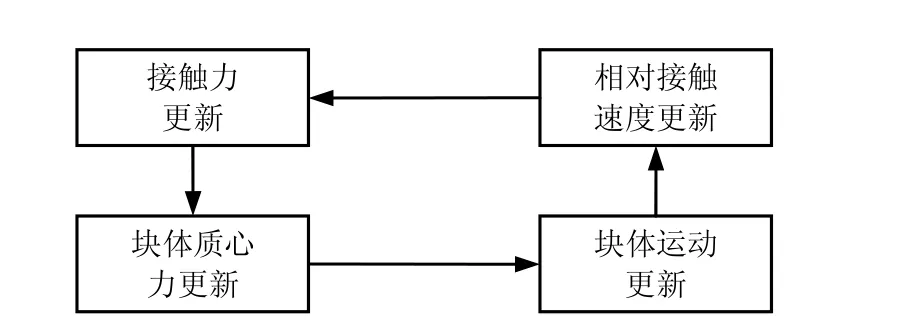
图2 计算循环[5]Fig.2 Calculation cycle[5]

整体坐标系下的平动方程为

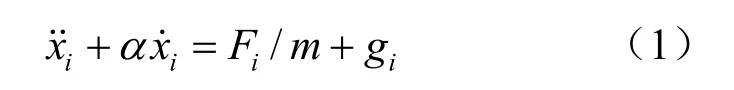
式中：m为块体质量； Fi为施加在块体上的合力分量(除重力外)，gi为重力加速度分量；x˙i为块体形心的平动速度；˙x˙i为块体形心的平动加速度；α为黏性阻尼常数。

用中心差分法可得

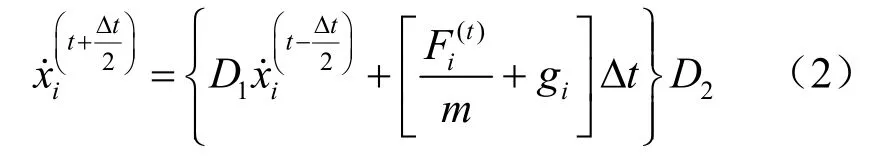
式中： D1=1 -(α Δt /2)；D2= 1/[1+ (α Δ t/2)]；t为计算时刻；Δt为时间步长。另外，块体的转动方程也可采用类似的方法求解，只要将平动速度换成转动速度，力换成力矩，质量换成转动惯量即可。

4 滑速的计算

滑坡体滑速的计算一直是个比较复杂的问题。在计算过程中，不仅要考虑滑坡体所在边坡的地形地貌、岩性特征和材料强度参数等条件，还要考虑滑坡体在运动过程中滑块受力条件和滑动面上的强度参数的变化等。因此，在实际工程应用中，常采用简化方法或经验公式法求滑坡体滑速，如能量守恒法、潘家铮法[11]、Scheidegger法[12]。

4.1 能量守恒法

如图3所示，根据动能定理有

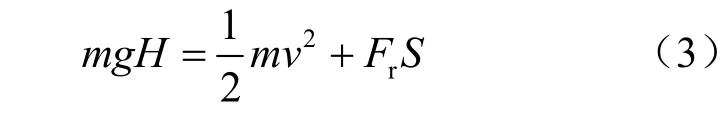
式中：g为重力加速度；H为块体的质心下落的竖直高度；v为块体速度；Fr为块体阻力；S为块体滑行长度。

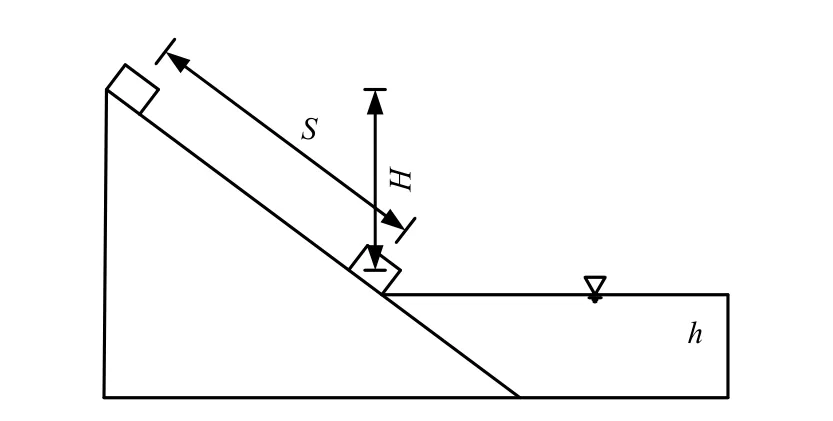
图3 块体滑动示意图Fig.3 Diagram of block sliding

又有

式中：c为黏聚力；f为内摩擦系数；A为块体与坡面的接触面积；N为块体受到坡面的反力。

求得

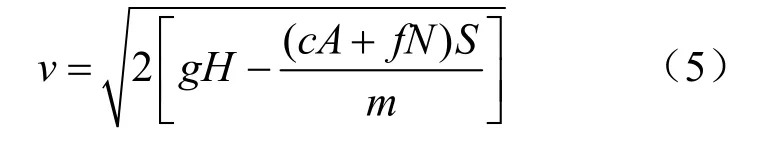
计算滑坡的速度采用能量守恒法是合适的，但得到的是某一平均高度滑坡岩土体的势能转化为动能的平均速度，而对滑坡体滑入水库时所激起的最大涌浪高度的估计往往要依赖于获得滑坡的最大速度，即需要求出滑坡局部岩土体运动到入水口前缘的速度，此时仍采用能量守恒法就不太合适。

4.2 潘家铮法

潘家铮法[11]把滑坡体作为质点系来研究其运动，考虑了加速度的变化。取滑坡开始下滑的瞬间为t0(t0= 0)，则t=ti时的滑坡水平速度为[11]

式中：vx为块体水平速度；ax为块体水平加速度；ΔL 为块体水平滑距，i为滑坡开始运动后的计算时刻标识（如共有n个时段，则i的取值可为0，1，…，n）。滑坡竖直速度的求法与水平速度类似，此时有ay=axtanαs，αs为坡面倾角。

潘家铮法在其推导公式的过程中假定各条块间完全无摩擦及其他阻力，这一假定可能导致偏于安全的结果。另外，要将该方法推广至三维情况则较繁琐。

4.3 Scheidegger法

由于内摩擦系数值在实际应用中不易选取，Scheidegger[12]在搜集了大量滑坡数据的基础上，进行了统计分析，发现滑坡体的等效内摩擦系数与滑坡体体积间有一定相关关系，给出的经验公式为[12]

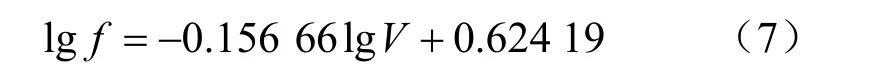
式中：f为等效内摩擦系数；V为滑坡体体积。

Scheidegger法避开了内摩擦系数值难以确定的问题，但其所求得的等效内摩擦系数只反映了滑坡规模的影响，而没有考虑到滑面材料参数的作用，如黏聚力和内摩擦角等，因此，与实际情况有出入。

4.4 离散元法

尽管滑坡体的下滑速度可通过能量守恒法或经验公式得到。但同时可以看出：滑坡体失稳后滑速发展过程极为复杂，各种计算方法都含有很多不确定因素，所得成果仅供定性研究之用。然而，离散单元法可以根据所需求解的基本公式（2）直接得到块体的速度，然后对时步进行积分，就可得到块体的位置，这样用离散单元法模拟滑坡运动时可直接获得任意时刻、任意块体的位置及滑速，为后续的涌浪计算提供了基础数据，与上述文献中给出的经验公式的方法相比，用离散单元法计算滑坡体的滑速具有更方便、更高效的特点。

4.5 算例考核

算例在xz剖面的几何尺寸如图4所示，y方向宽为20 m，块体尺寸为m× 1 m× 1 m。计算参数为时间步长 Δt = 10-5s ，总时间步长为 106步，边界面的法向刚度 Kn= 1010N/m3，切向刚度Ks=4.0× 109N/m3，块体重度 γ= 20.0 kN/m3，接触面上的黏聚力为2 kPa，内摩擦角为10°。

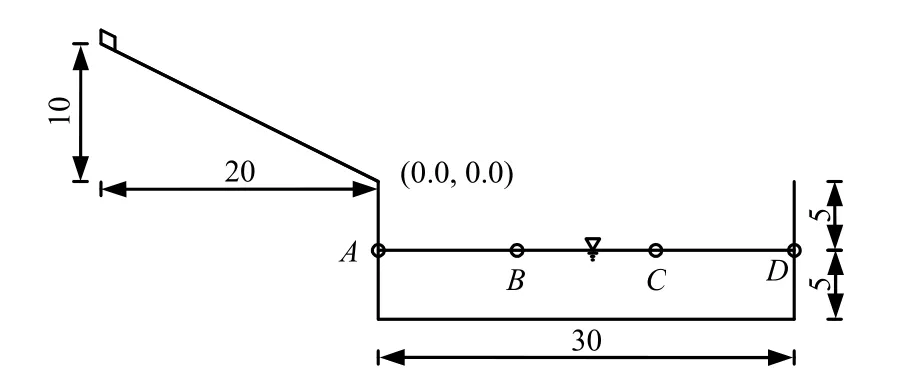
图4 滑坡算例 (单位: m)Fig.4 A landslide example (unit: m)

图5给出了能量法、潘家铮法和离散单元法计算块体在坡面上滑行前3 s的速度，离散单元法计算中每1 000时步（即0.1 s）输出一次结果，输出的块体位置结果当作能量法、潘家铮法的计算条件，能量法和潘家铮法所需要的其他计算参数见图4及计算参数说明，速度方向为沿着坡面方向。从图中可以看出，离散单元法的结果与能量法和潘家铮法一致性较好，这说明程序中块体与边界面的接触判断、接触力的计算是正确的。同时可以在计算过程中看出，能量守恒法通常只能得到块体在某一具体位置时的滑速，而要得到任意时刻的块体速度则计算较繁琐；潘家铮法则需要将整个计算时段划分成很多小的时段以精确地模拟加速度的变化，采用手工计算时计算量较大。

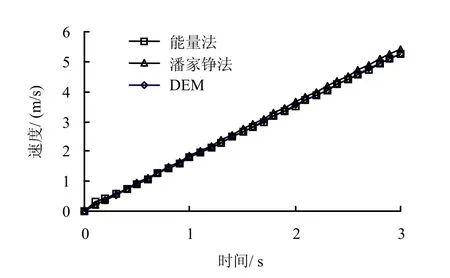
图5 各方法的滑坡体速度比较(c = 2 kPa, φ = 10°)Fig.5 Comparative results of block velocity (c = 2 kPa, φ = 10°)

5 涌浪的计算

当失稳后的滑坡体进入水库中时，将产生涌浪。涌浪以滑坡体入水处为源点，先向对岸传播，然后通过波的扩散和反射，引起一个向上游和下游传播的过程[11]。要评价库岸滑坡涌浪对附近建筑物的危害性，首先需要估算出涌浪到达各建筑物处的浪高。然而，这是一个相当复杂的过程，不容易求得精确解。在实际工程应用中，估算法用得较多，广泛采用的有 Noda[13]提出的推算法和潘家铮[11]提出的近似估算法。

5.1 Noda法

Noda法[13]假定滑坡体滑落于半无限的水体中，且下滑高程大于水深。根据重力表面波线性理论，推导出滑坡引起的涌浪高度计算公式。其最大涌浪高度的表达式为[13]

式中：hmax为最大涌浪高度；h为水深；vs为滑坡体进入水库时的速度。

从式（8）中可以看出，Noda法估算最大涌浪高度时主要考虑的因素是滑坡滑速，两者呈线性关系。此外，最大涌浪高度还与水深有一定关系，水越深，滑坡体所激起的涌浪高度越高。

5.2 潘家铮法

潘家铮[11]认为，对于各种类型的滑坡只要确定其岸坡变形速率和过程以及反射特性后，均可用数值法求出涌浪过程。其基本假定为：①涌浪首先在滑坡入水处发生，产生初始波，然后向周围传播，假定传播过程中涌浪能量损耗为已知；②不考虑边界条件的非线性影响，整个涌浪过程可以视为在源点处产生的一系列小波的线性叠加；③每个小波都是孤立波，且以常波速在水面上传播；④库岸对涌浪的反射系数为已知值；⑤水库库岸为两条平行陡壁，滑坡范围内的库岸断面一致，滑坡变形率dA/dt或滑速v(t)为常数。

根据以上假定，可求得涌浪正对岸某点A的最大涌浪高度为

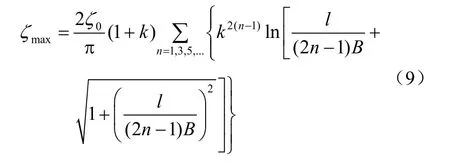
式中：ζmax为最大涌浪高度；ζ0为初始波高；k为波的反射系数；l为滑坡半长；B为滑坡体入水口至对岸点的距离。

波速c可按下式计算：

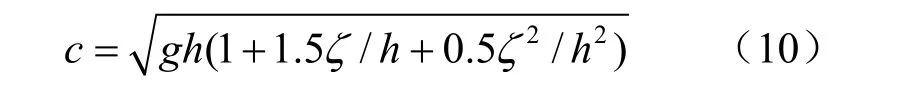
式中：ζ为波高。

初始波高ζ0可以通过下面的方法得到，对于水平岸坡变形情况：对于垂直岸坡变形情况：当时，当时，ζ0/λ呈曲线变化；当时， ζ0/λ =1；λ为滑坡的厚度。

在国内，潘家铮法用得较多，但潘家铮法只能给出某点处某一时刻所能达到的涌浪最大高度，而不能给出任意时刻涌浪的高度及形态。鉴于块体的规模比水库的库容小得多，为了更好地模拟涌浪的形态，本文采用潘家铮法计算滑坡入水口处的初始涌浪，然后将其作为初始条件直接用二维波动方程求解涌浪在各个时刻的形态，边界条件为如图4所示的水库边界，其涌浪值一开始为 0，后续的值通过差分计算得到，这样可以模拟水波的反射。含黏性阻尼的小振幅二维波动方程为[14]

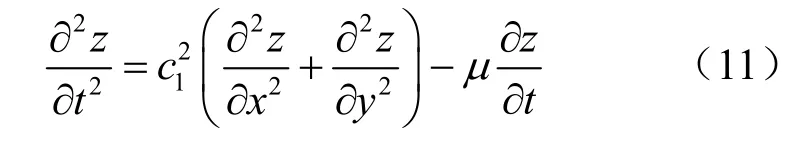
式中：z为波高；c1为波速；μ为流体的黏度。采用显式差分格式进行求解。

5.3 算例考核

计算参数同4.5节的算例，取图4中的A、B、C、D为涌浪计算的特征点。

图6中给出了一个块体滑入水库时所产生的涌浪在特征点处的涌浪高度的历程曲线。从图可以看出，特征点A处最早达到第1次涌浪峰值为0.098 m（在6.09 s时），因为A点的x坐标为0 m，距离块体入水口的x坐标4 m最近，但同时可以看出，特征点A处在前10 s的最大涌浪高度是在7.29 s时的0.187 m，这说明涌浪在水库某处取得最大值不一定在滑坡体刚失稳时，而有可能在涌浪反射后叠加时取得。

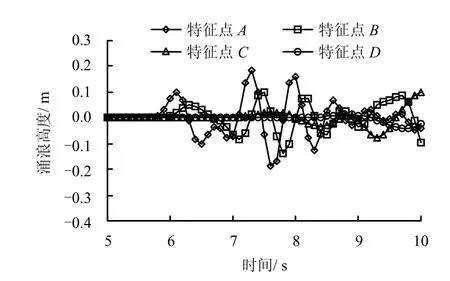
图6 一个块体失稳时特征点处涌浪高度-时程曲线Fig.6 Relationships of surge height and time of characteristic points after one block failure

表1中给出了一个块体失稳时潘家铮法与本文的涌浪计算结果。从表中可以看出，本文的涌浪计算结果与潘家铮法计算结果较接近，能满足实际需求。另外，本文中的涌浪计算可获得任意时刻的涌浪计算结果，比潘家铮法更方便。

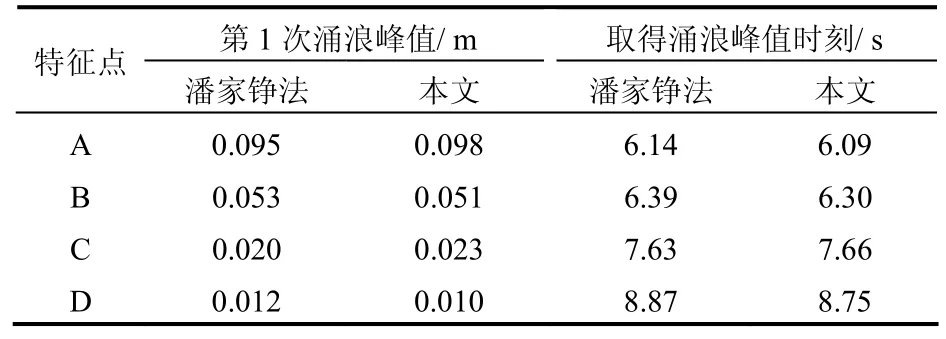
表1 涌浪计算结果比较Table 1 Comparative results of surge

图7中给出了3个块体滑入水库时所产生的涌浪在特征点处的涌浪高度的历程曲线。与图6相比，由于涌浪的叠加，3个块体所激起的涌浪高度比 1个块体所激起的涌浪高很多，这说明在考虑滑坡所激起的涌浪时要考虑到多块体下落的叠加效应，涌浪的最大值很可能出现在几个涌浪值不大的块体失稳后的叠加时刻。

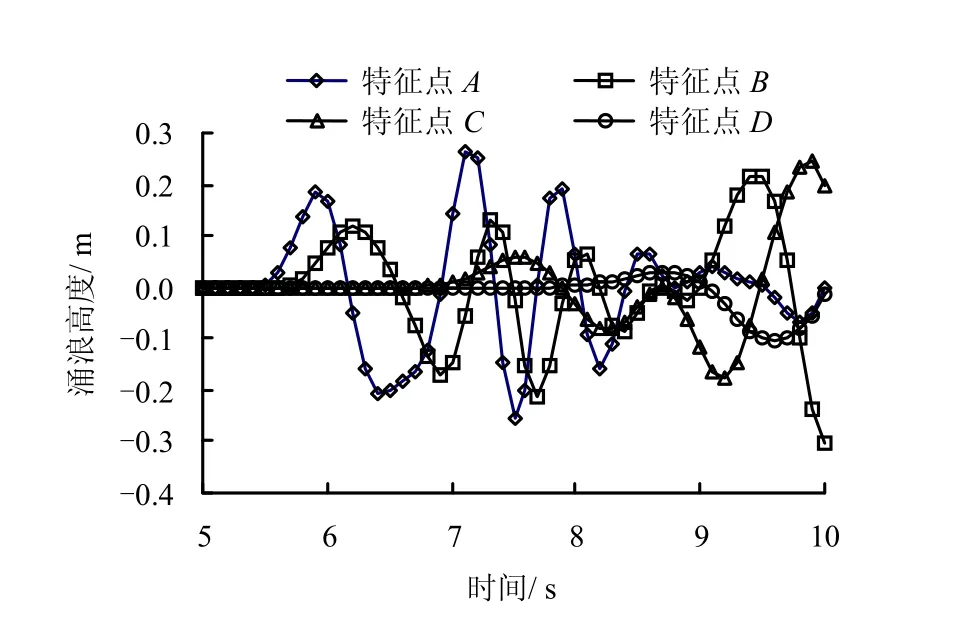
图7 3个块体失稳时特征点处涌浪高度-时程曲线Fig.7 Relationships of surge height and time of characteristic points after three blocks failure

图8、9分别给出了1个块体和3个块体失稳后7 s时的涌浪位置及形态（由于涌浪值较水库的尺寸较小，图中显示涌浪高度值时采用的放大比例为5倍）。从图中可以看出，结合离散单元法所提供的滑坡体的运动速度等基础数据，采用潘家铮法和波动方程相结合对涌浪进行估算能给出滑坡体所激起的较合理的涌浪形态，为滑坡失稳所造成的灾害评估提供了理论依据。

6 滑坡堆积计算

大型滑坡失稳后会堵塞河道，从而影响航运的正常运行，如果滑坡离电站进水口较近时，还会影响电站的正常工作。为了更好地对滑坡灾害进行评估，对滑坡的运动轨迹及堆积形状的模拟是至关重要的。

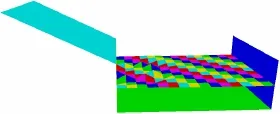
图8 1个块体失稳后产生的涌浪 (t=7.0 s)Fig.8 Surge shape after one block failure (t=7.0 s)

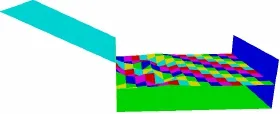
图9 3个块体失稳后产生的涌浪 (t=7.0 s)Fig.9 Surge shape after three blocks failure (t=7.0 s)

6.1 基本原理

离散单元法基于牛顿第二定律进行求解，每次求解前需要根据前一时刻给出的块体位置进行接触判断，然后求得本时步各个块体的位置信息。根据离散元所求解的基本公式（2）可以直接得到块体的速度，然后对时步积分就可得到块体的位置，这样就得到了块体的堆积形状。

6.2 算例考核

算例在xz平面的几何尺寸同4.5节中的图4，y方向宽20 m；块体尺寸为：x方向长4 m，y方向宽为4 m，z方向高为5 m。计算参数为：时间步长Δt = 10-5s，总时间步长为 1.5×106步，边界面的法向刚度 Kn= 1010N/m3，切向刚度 Ks=4.0 ×109N/m3，块体重度 γ= 20.0 kN/m3，接触面上的黏聚力为2 kPa，内摩擦角为10°，黏性阻尼常数α=1.0。不同时刻块体的堆积形状如图10所示。从图中可以看出，离散单元法能给出滑坡运动后较合理的堆积形状。

7 结 论

（1）在水库库岸滑坡涌浪的分析中，失稳后滑坡体的滑速及规模是分析的基础，其值准确与否的关键在于如何正确获得滑坡体的运动速度、运动轨迹及堆积形状等数据，离散单元法可以直接得到上述数据。

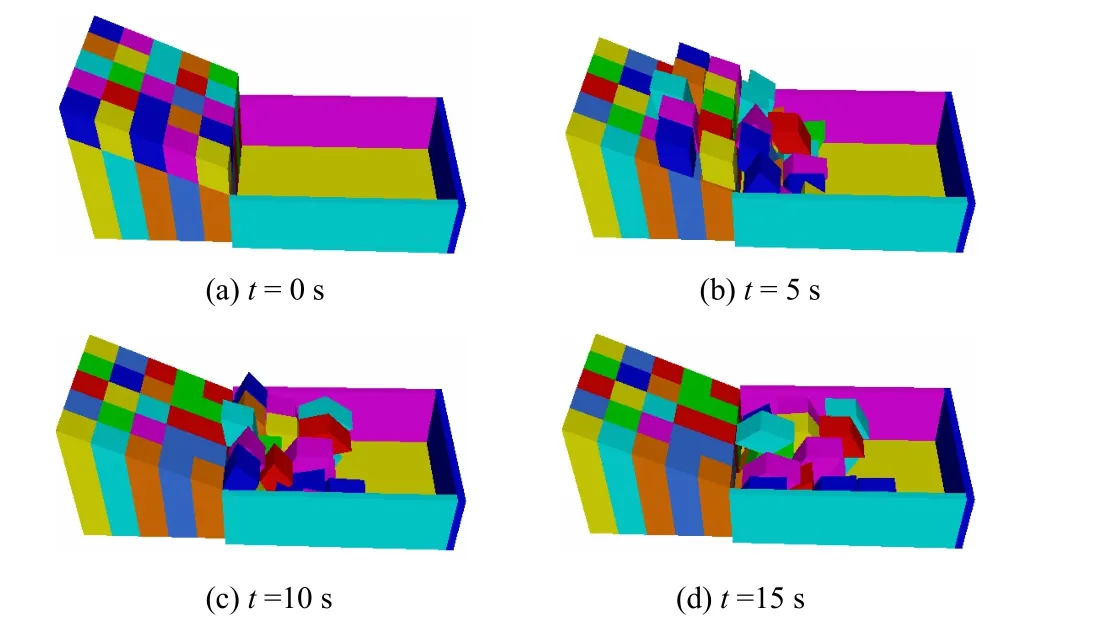
图10 不同时刻块体的堆积形状Fig.10 Heap shape of blocks at different times

（2）离散单元法不仅能达到与能量法和潘家铮法同样的精度，而且计算滑坡体的滑速具有更方便、更高效的特点，且能获得任意时刻块体的位置与滑速。

（3）当滑坡体滑入水库中时，结合离散单元法所提供的滑坡体的运动速度等基础数据，并采用涌浪估算的潘家铮法和求解波动方程能给出滑坡体所激起的较合理的涌浪形态。

（4）从涌浪的计算结果来看，在涌浪分析中要特别注意涌浪的叠加现象，涌浪的最大高度很可能出现在几个规模不大的滑坡体失稳后的叠加时刻。

（5）由边坡的动态破坏过程可知，边坡在失稳前一般都会表现出一定的预兆，如沿坡面向外的位移或速度的持续增大。因此，对边坡加强安全监测和动态跟踪是非常必要的。

（6）由于初步研究，涌浪的计算主要是根据经验公式得到的，若要更好地模拟滑坡入水后涌浪的形状、衰减规律和反射情况应采用离散单元法与计算流体力学耦合的方法，这有待于进一步的研究。

[1]黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报, 2007, 26(3): 433－454.HUANG Run-qiu. Large-scale landslides and their sliding mechanisms in China since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007,26(3): 433－454.

[2]郑颖人, 赵尚毅, 邓卫东. 岩质边坡破坏机制有限元数值模拟分析[J]. 岩石力学与工程学报, 2003, 22(12):1943－1952.ZHENG Ying-ren, ZHAO Shang-yi, DENG Wei-dong.Numerical simulation on failure mechanism of rock slope by strength reduction FEM[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12): 1943－1952.

[3]汪洋, 殷坤龙. 水库库岸滑坡初始涌浪叠加的摄动方法[J]. 岩石力学与工程学报, 2004, 23(5): 717－720.WANG Yang, YIN Kun-long. Perturbation method of superposing initial surge height of landslide along reservoir shoreline[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 717－720.

[4]CUNDALL P A. A computer model for simulating progressive, large-scale movements in blocky rock systems[C]//Proceedings of the International Symposium on Rock Mechanics. Nancy: [s. n.], 1971.

[5]ITASCA Consulting Group, Inc. 3DEC－3 Dimensional distinct element code (version3.0), user’s manual[R].Minneapolis: ITASCA Consulting Group, Inc., 2007.

[6]焦玉勇, 葛修润, 刘泉声, 等. 三维离散单元法及其在滑坡分析中的应用[J]. 岩土工程学报, 2000, 22(1): 101－104.JIAO Yu-yong, GE Xiu-run, LIU Quan-sheng, et al.Three-dimensional discrete element method and its application in landslide analysis[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(1): 101－104.

[7]LEMOS J A. A distinct element model for dynamic analysis of jointed rock with application to dam foundation and fault motion[D]. St. Paul: University of Minnesota, 1987.

[8]周晓青, 王元汉, 哈秋舲. 离散单元法与边界单元法的外部耦合计算[J]. 岩石力学与工程学报, 1996, 15(3):231－235.ZHOU Xiao-qing, WANG Yuan-han, HA Qiu-ling.External coupling computation between distinct element method and boundary element method[J]. Chinese Journal of Rock Mechanics and Engineering, 1996,15(3): 231－235.

[9]王泳嘉, 邢纪波. 离散单元法及其在岩土力学中的应用[M]. 沈阳: 东北工学院出版社, 1991.

[10]张楚汉. 岩石和混凝土离散-接触-断裂分析[M]. 北京:中国水利水电出版社, 2008.

[11]潘家铮. 建筑物的抗滑稳定与滑坡分析[M]. 北京: 水利出版社, 1980.

[12]SCHEIDEGGER A E. On the predication of the reach and velocity of catastrophic landslides[J]. Rock Mechanics,1973, 5(4): 231－236.

[13]NODA E. Water waves generated by landslides[J].Journal of Waterways, Harbors and Coastal Engineering Division, ASCE, 1970, 96(4): 835－855.

[14]庞明勇. 基于离散模型的二维水波实时动态模拟方法[J].水利学报, 2007, (11): 1358－1363.PANG Ming-yong. Realtime dynamic simulation of 2D water waves based on discrete model[J]. Journal of Hydraulic Engineering, 2007, (11): 1358－1363.