对“预应力锚杆柔性支护体系的锚杆抗拔力研究”的讨论
廖 军
(西南交通大学 土木工程学院,成都 610031)
笔者拜读了贵刊2012年第33卷第2期由周勇和朱彦鹏撰写的《预应力锚杆柔性支护体系的锚杆抗拔力研究》[1](以下简称文献[1])一文。现有以下几点望与文献[1]作者商讨。
(1)锚杆轴向静摩擦力
文献[1]在 3.2.1节锚杆力学分析中提到“如果锚杆不受拔力,即拔力P=0,由图2(b)可知,锚杆所受静摩擦力F的作用方向与拔力方向一致”,笔者认为锚杆所受静摩擦力F的作用方向值得商榷。由物理学知识可知,物体所受静摩擦力方向与该物体的运动趋势方向相反,如果说“锚杆所受静摩擦力F的作用方向与拔力方向一致”,则锚杆存在与拔力方向相反的运动趋势,而锚固体在土体中各个方向的边界条件都是受限制的,尤其是锚固体的尾部更是受到约束作用,不可能存在与拔力方向相反的运动趋势,那么“锚杆所受静摩擦力方向与拔力方向一致”值得进一步商榷。
关于锚杆静摩擦力F的计算公式,文献[1]式(3)为 P + F = E sin α,此公式值得商榷。文献[1]在文中提到“满足条件 P<E sinα,此时静摩擦力F随拔力P的增大逐渐减小,且其方向与拔力方向一致;当满足条件 P>E sin α,静摩擦力开始反向作用提供抗拔力”,根据文献[1]的说法,静摩擦力F的方向在锚杆支护期间存在一个反向的过程,而锚杆所受轴向拔力P的方向始终是保持不变的,则文献[1]中式(3)应该考虑锚杆拔力与锚杆轴向静摩擦力方向可能不同的影响,笔者认为如果采用矢量表述或适当加以条件限制来改写式(3)更为妥当。
笔者认为文献[1]的式(3)的正确性有待深入研究。由式(3)可知,竖直方向的上覆土压力E产生的沿锚杆轴向的分力Esinα由拉拔力p和锚杆轴向静摩擦力F来平衡。从锚杆剖断面图(如图 1所示)可以看出,取厚度为锚固体直径的土条ABCD-A′B′C′D′,锚固体上方的Esinα还需要由锚固体上方土条两侧面 ABCD 和 A′B′C′D′上的摩擦力来平衡一部分。另外,由图 1可以看出,第i土条产生的dE⋅sinα还会作用在第i+1土条上,而土条间的相互作用力在文献[1]的式(3)中没有体现出来,文中也没有相关假设或文字对土条间的相互作用力进行说明。

图1 锚杆剖断面图Fig.1 Section of anchor
(2)土体自承作用抗拔力
文献[1]认为“锚杆的上覆土压力的轴向分力E sinα通过锚杆作为传力构件始终作用于锚杆的抗拔全过程,这种抗拔力由锚杆上覆土体自重作用产生,称其为土体自承作用抗拔力”,笔者认为“Esinα通过锚杆作为传力构件始终作用于锚杆的抗拔全过程”略有不妥。早在1936年,Terzaghi就通过著名的活动门试验[2]证实了岩土工程中土拱效应的存在,并得出了其存在的条件:①土体之间产生不均匀的位移或相对位移;②有作为支撑的拱脚的存在。Terzaghi还于1943年将土拱效应定义为土中应力由屈服土体向邻近未屈服土体转移的现象。因此,锚杆在成孔过程中,由于锚固体范围内的土体被掏空,孔壁处的应力状态与初始状态相比,出现一个卸荷过程,孔壁周边的应力出现重分布现象,形成土拱效应,土拱将孔壁上方的土压力转移到孔壁两侧,从而维持孔壁的稳定(对于砂土等特殊情况,如果塌孔需另当别论,这里不做讨论)。因此,钻孔完毕后,上覆土压力的轴向分力Esinα主要由后侧相邻土体和两侧土体来承担。在钻孔中设置锚杆并注浆后,如果是无压注浆(重力注浆),可以认为注浆体和孔壁只存在接触,锚固体不会承担上覆土压力的轴向分力Esinα,锚固体的抗拔力主要由注浆体与孔壁间的握裹咬合力来承担。如果是高压注浆,则会增加注浆体与孔壁间的正应力,从而提高握裹咬合力,由于锚杆不存在向下的运动趋势,所以在锚杆受拉力作用前,锚杆轴向静摩擦力F应该是不存在的。因此,土体的自承作用抗拔力也是不存在的,则文献[1]中的式(3)将不成立。
(3)锚土作用抗拔力
文献[1]中 3.2.2节中第 j排锚杆延长位置x处dx微段上由锚土作用提供的抗拔力(原文式(5))表示为
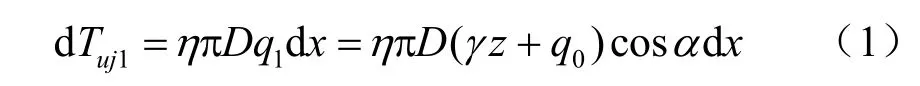
积分求得第j排锚杆由锚土作用提供的抗拔力Tuj1(原文式(7))为
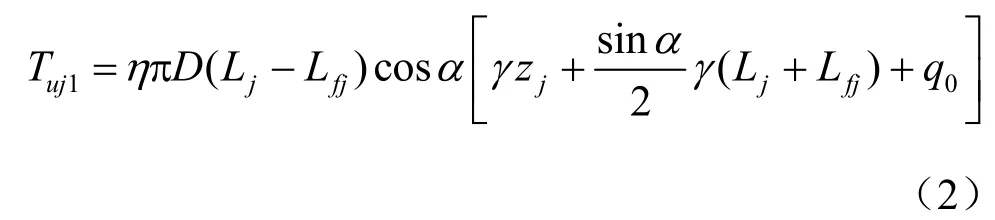
式(2)可变形为

而文献[1]中式(1)为

式中: τ = c + σtan φ。
对比式(3)和式(4)可得
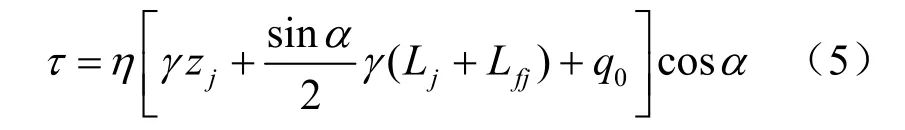
式(4)为《建筑基坑支护技术规程》[3]中关于锚杆抗拔力的计算依据。由式(5)可以看出,文献[1]关于锚土作用抗拔力的计算实质上是将规范中锚固段周边砂浆与孔壁的平均抗剪强度采用锚固段中点上覆土压力沿锚固段的垂向分量与锚固体和土体间的摩阻力系数的乘积来替换,对同一排锚杆,规范[3]中的锚固段周边砂浆与孔壁的平均抗剪强度以及文献[1]中锚固体与土体之间的摩阻力均为常数,或者说二者选用的摩阻力沿锚固段长度都呈均匀分布。因此,文献[1]中锚土作用抗拔力和规范[3]的传统解法本质应该是一样的。问题在于,诸多研究[4-7]都表明,锚固体与土体间的摩阻力并不是均匀分布的,而是在其前端形成峰值,逐步向末端减少并最终趋近于 0,且主要分布在锚固段前端(拉力型锚杆)按均匀分布模式计算是不太合适的。
(4)规范解法与文献[1]解法对比
文献[1]中第4.3节“在实际工程计算分析中,目前还是较多地采用传统方法计算锚杆的抗拔力,这显然偏于保守。这一点充分解释了为什么有时由于地质条件的原因导致锚杆的施工长度达不到设计长度,但基坑或边坡仍然比较稳定的现象”。正如前文所说,锚固段摩阻力的分布是不均匀的,因此,当锚固段长度在一个合理的长度范围内时,理论上按照摩阻力非线性分布求解的锚杆抗拔力和规范法[3]按均匀分布求解的锚杆抗拔力是有可能相等的。但是,当锚固长度过长时,由于摩阻力非线性分布,较远部分的锚固体可能不能充分发挥作用(锚杆存在临界锚固长度[8-9],锚杆抗拔力不随锚杆长度线性增加),此时仍按照摩阻力均匀分布求解,可能计算得出锚杆抗拔力大于实际抗拔力的不利结果。另外,文献[1]说规范法保守,是因为文献[1]计算锚杆抗拔力时,还考虑了土体自承作用抗拔力,而正如前文所分析的,土体自承作用抗拔力是否存在还有待商榷。
另外,即使传统法计算锚杆抗拔力偏于保守,也不能“充分解释了为什么有时由于地质条件的原因导致锚杆的施工长度达不到设计长度,但基坑或边坡仍然比较稳定的现象”。根据规范[3]可将锚杆轴向抗拔力N与锚杆支点力计算值Tc表达如下:
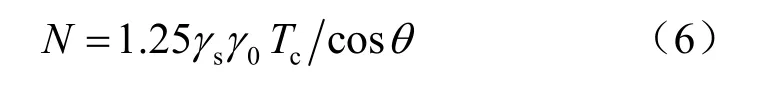
式中:γs为锚杆轴向受拉抗力分项系数,可取1.3;γ0为基坑侧壁重要性系数,按基坑侧壁安全等级1~3级分别取1.1、1.0、0.9。也就是说,按照规范[3]对锚杆进行设计时,锚杆轴向抗拔力为锚杆轴向力计算值的1.787 5倍(1级基坑)、1.625 0倍(2级基坑)、1.462 5倍(3级基坑)。可以看出,即使由于地质条件原因导致锚杆施工长度达不到设计长度,也可能会因为锚杆设计时选用了较大的安全储备(尤其是1级基坑),而使得基坑或边坡仍然处于比较稳定的现象,只不过此时的安全系数略有降低而已。另外,当锚杆长度设计过长时,也可能因为没有施工的那部分锚杆实际发挥作用很小(按实际摩阻力非线性分布考虑),对锚杆总抗拔力影响不大,从而不足以影响基坑或边坡的稳定性。还有,当锚固体水泥浆采用高压注浆时,也会增大锚固体与土体间的摩阻力,从而提高锚杆抗拔力。因此,笔者觉得不能按规范法计算锚杆抗拔力偏于保守来“充分解释了为什么有时由于地质条件的原因导致锚杆的施工长度达不到设计长度,但基坑或边坡仍然比较稳定的现象”。
文献[1]考虑土体自承作用抗拔力和直接采用规范法分别得到的算例1和算例2中不同锚杆的抗拔力对比如表1和表2所示。
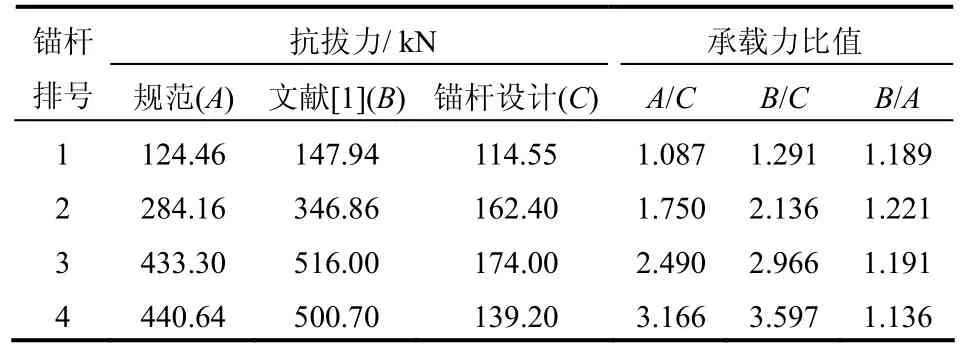
表1 算例1规范与文献[1]抗拔力对比(单位:kN)Table 1 Comprasion of calculated anti-pulling force between code and Ref.[1]in case 1 (unit: kN)

表2 算例2规范与文献[1]抗拔力对比(单位:kN)Table 2 Comprasion of calculated anti-pulling force between code and Ref.[1]in case 2 (unit: kN)
从表1和表2中可以看出,考虑土体自承作用抗拔力得到的锚杆总抗拔力比按规范计算的抗拔力高出约14%~22%,但是按照规范法得到的锚杆抗拔力均大于锚杆设计承载力,都满足设计要求。因此,结合前文所述,在未能充分研究清楚土体自承作用抗拔力的机制前,有可能会出现考虑土体自承作用抗拔力得到的锚杆实际总抗拔力小于锚杆设计承载力的不利情况。综上所述,在计算锚杆的总抗拔力时,笔者建议不宜考虑土体自承作用抗拔力。
[1]周勇, 朱彦鹏. 预应力锚杆柔性支护体系的锚杆抗拔力研究[J]. 岩土力学, 2012, 33(2): 415-421.ZHOU Yong, ZHU Yan-peng. Research on anti-pulling force of anchor of flexible supporting system with prestressed anchors[J]. Rock and Soil Mechanics, 2012,33(2): 415-421.
[2]TERZAGHI K. Theoretical soil mechanics[M]. New York:John Wiley & Sons, 1943.
[3]中华人民共和国行业标准编写组. JGJ120-99 建筑基坑支护技术规范[S]. 北京: 中国建筑工业出版社,1999.
[4]何思明, 李新坡. 预应力锚杆作用机制研究[J]. 岩石力学与工程学报, 2006, 25(9): 1876-1880.HE Si-ming, LI Xin-po. Study on mechanism of prestressed anchor bolt[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(9): 1876-1880.
[5]蒋忠信. 拉力型锚索锚固段剪应力分布的高斯曲线模式[J]. 岩土工程学报, 2001, 23(6): 696-699.JIANG Zhong-xin. A Gauss curve model on shear stress along anchoring section of anchoring rope of extensional force type[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(6): 696-699.
[6]尤春安, 战玉宝. 预应力锚索锚固段应力分布规律及分析[J]. 岩石力学与工程学报, 2005, 24(6): 925-928.YOU Chun-an, ZHAN Yu-bao. Distributing characters and analysis of stresses in prestressed cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(6): 925-928.
[7]徐景茂, 顾雷雨. 锚索内锚固段注浆体与孔壁之间峰值抗剪强度试验研究[J]. 岩石力学与工程学报, 2004,23(22): 3765-3769.XU Jing-mao, GU Lei-yu. Testing study on the peak shear strength between grout and bore wall in the interior bond section of prestressed anchorage cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2004,23(22): 3765-3769.
[8]龙照, 赵明华, 张恩祥, 等. 锚杆临界锚固长度简化计算方法[J]. 岩土力学, 2010, 31(9): 2921-2925.LONG Zhao, ZHAO Ming-hua, ZHANG En-xiang, et al.A simplified method for calculating critical anchorage length of bolt[J]. Rock and Soil Mechanics, 2010, 31(9):2921-2925.
[9]张洁, 尚岳全, 叶彬. 锚杆临界锚固长度解析计算[J].岩石力学与工程学报, 2005, 24(7): 1134-1138.ZHANG Jie, SHANG Yue-quan, YE Bin. Analytical calculations of critical anchorage length of bolts[J].Chinese Journal of Rock Mechanics and Engineering,2005, 24(7): 1134-1138.

