危险品运输的集中管理模型*
彭姗姗 孙会君
(北京交通大学交通运输学院 北京 100044)
0 引 言
在危险品运输的研究中,主要考虑的两大问题是风险分析和网络优化,本文主要考虑网络优化问题.国内外不少学者就危险品运输的风险分析和路线优化进行了研究.风险分析方法有定量分析和定性分析2种,最常用的是“传统风险”模型[1].在路线优化方面,Erkut和 Gzara[2]针对政府指定危险品运输网络及运营商选择路线问题建立双层规划模型,该模型考虑运输成本与风险的权衡,以运输成本为上层目标.Kara和Verter[3]建立了一个基于路径的危险品运输设计模型,在该模型中,政府关闭某些路段从而使网络中的总风险最小.Kazantzi等[4]采用最小费用流网络问题的思想来研究危险品运输路线优化问题,以尽量减少运输成本和降低风险为目标,在满足需求的条件下寻求最优的运输路线.魏航[5]研究了时变条件下单一运输方式有宵禁的危险品运输最短路问题,建立了时变条件下有到达时间约束、具有多个出发时间和有软、硬宵禁限制的危险品运输最短路模型.
在现实的危险品运输过程中,如果政府不对运输者进行管理,运输者在选择路径时不会考虑系统的风险,而只考虑自身的出行时间最优,有可能造成风险过大,而政府一般要考虑社会风险,则有可能损失运输者的利益.所以,危险品运输中必须要有政府的管理,然而政府在集中管理时,不仅要从自身的利益出发最小化网络总风险,也要从运输者的角度出发约束网络中的总出行时间在一定范围之内,从而使得运输者愿意接受政府的统一安排.本文就是基于这样的思想而展开研究的,在定义危险品运输风险时,采用“传统风险”模型并以暴露人口作为事故所造成损失;在建立了路径选择模型时,以网络总风险最小为目标函数,并约束网络中的总出行时间.在建立路径选择模型之前,先定义危险品运输风险.
1 风险定义
在危险品运输风险分析研究中,大多数学者采用“传统风险”(traditional risk)模型,他们认为危险品运输风险等于事故发生的概率与事故所造成损失的乘积[6].
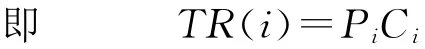
式中:TR(i)为危险品运输风险;Pi为事故发生概率;Ci为事故所造成的损失.
首先,定义路段a发生危险品运输事故的概率为
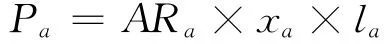
式中:ARa为路段a单位危险品车辆单位距离的事故概率;xa为路段a危险品车辆数;la为路段a长度.
根据“传统风险”模型定义路段a的风险为
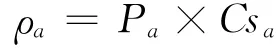
式中:Csa为路段a事故发生时的暴露人数,即路段a事故所造成的损失.
2 路径选择模型
危险品运输的路线优化主要是研究如何降低运输网络中的风险,同时使运输网络的总费用最小.本文假设政府有权利安排每辆车的行驶路线,即政府集中管理网络中的危险品车辆.在此假设的基础之上,建立统一安排危险品车辆的系统最优模型.由于风险最小是政府考虑的目标,运输车辆本身不会有这样的目标,实现政府目标的危险品管理模式是集中管理模式,而只从运输者角度考虑运输时间(或距离等)最小的模式为分散管理模式.本文所建立的模型以风险最小为目标体现了政府的集中管理,为危险品运输的集中管理模型.模型以网络中的总风险(暴露人口)最小为目标函数,为了运输者能接受政府的统一安排,运输者的总出行时间不超过运输者在无政府状况下按UE(用户均衡)原则选择路径时的总出行时间的θ倍.
基于此,建立的路径选择模型为
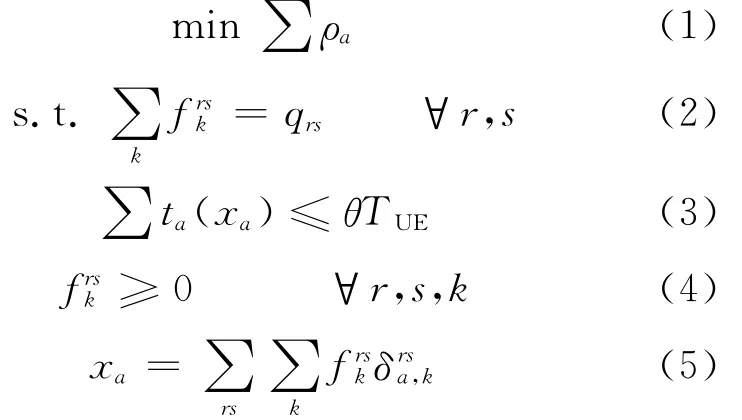
其中:式(1)为目标函数,即政府使网络中的总风险(暴露人口)最小,式中:ρa为路段a的风险,由风险定义给出.式(2)为运输网络的需求约束,即OD对rs间所有路径的流量之和等于rs间的总需求,其中frsk,qrs分别代表危险品车辆的路径流量和需求;式(3)为政府从运输者的角度考虑,使运输者的总出行时间不超过运输者在无政府状况下按UE(用户均衡)原则选择路径时的总出行时间(TUE)的θ(θ≥1)倍,从而使得运输者能接受政府的统一安排,其中:xa为路段a危险品车辆数,ta(xa)采用BPR函数[7]形式,即ta=t0a(1+α(xa/Cij)β),t0a为路段a 的0流阻抗,α,β为回归系数;式(4)为非负约束,即危险品车辆的路径流量frsk应为非负;式(5)为运输网络中路段流量与路径流量之间的关系式,如果路段a在OD对rs的第k条路径上,则δrsa,k=1,否则δrsa,k=0.
3 算法设计
针对建立的危险品车辆流量分配模型,本文设计了相应的粒子群算法来进行求解.算法的思想是构造路线条数维的粒子空间,每一维对应一条可行性路线,其值为对应路线所分配的交通量,为使交通量守恒,应对粒子进行归一化处理,并进行交通量的多路径分配.根据目标函数评价与筛选粒子,直到满足终止条件.参照基本粒子群算法[8],设计求解本文模型的粒子群算法步骤为
步骤1 初始化.设置群规模m;最大速度V;最大迭代次数T;计算学习因子c1,c2;惯性权重 w 的参数c1f,c2f,c1i,c2i,w_max,w_min.并初始化粒子的位置和速度[9].在此,粒子的位置向量yi取[0,qlrs]之间的随机数,即表示路径流量的取值为=qrs×rand,为保证交通量守恒,需对其进行归一化处理=qrs/∑,每一维粒子的初始飞行速度取Vi=V×rand.
步骤2 评价粒子.用目标函数评价每一个粒子的适用值.
步骤3 更新最优.(1)比较粒子的当前适用值与个体最优值pbest,如果优于个体最优值pbest,则将当前位置记为个体历史最优位置pid;(2)比较粒子当前适用值与群体全体最优值gbest,若优于gbest,则群体最优位置pGd就是当前粒子位置;(3)根据群体最优位置pGd及式(3)计算得到xa.
步骤5 循环回到步骤2,直到达到最大迭代次数.
4 算例分析
如图1所示,1为网络的起点、6为终点.网络中共有9条路段,取m=80,T=1 000,c1f=c2i=2.5,c1i=c2f=0.5,w_max=1.4,w_min=0.4,V=4,α=0.15,β=4,qrs=100pcu/min,其他参数见表1.
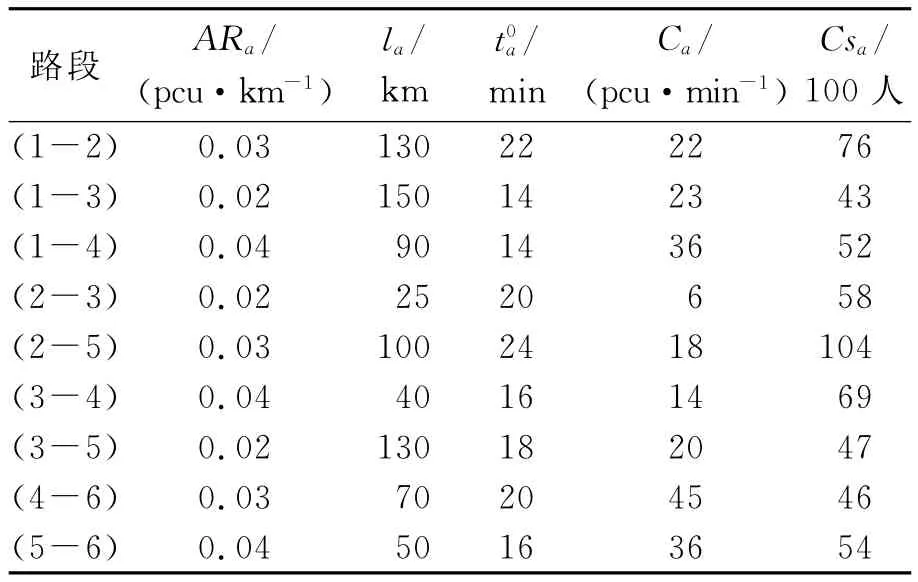
表1 算例参数
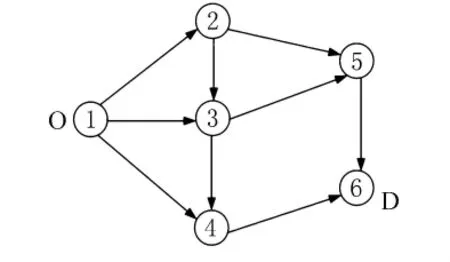
图1 算例网络图
首先计算无政府状态下网络中的总出行时间,此时运输者按UE(用户均衡原则)进行路径选择,根据用户平衡交通分配模型及F-W算法可计算得到,用户均衡条件下网络中的总出行时间为6 508.81min.
根据设计的粒子群算法,采用Matlab编程,得到网络危险品总需求为θ=1.5时的迭代收敛图如图2.由图2可见,程序经过多次运行,算法在迭代20次后,目标函数值保持稳定,说明算法在迭代了20次后就开始收敛,所以本文采用的粒子群算法在计算所建立的模型上是收敛、有效的.
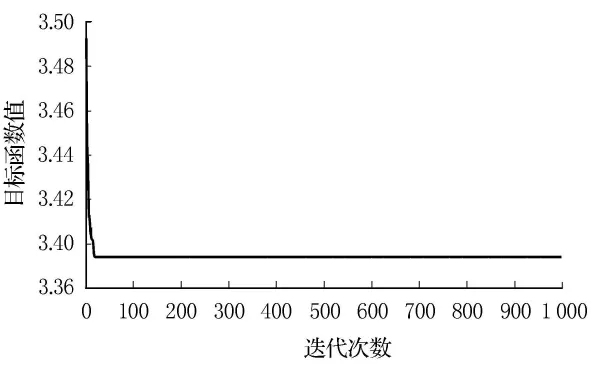
图2 算法迭代收敛图
约束式(3)中的θ表示了政府与运输者之间的权衡,θ的大小反映出了政府考虑运输者利益的程度.为了分析θ的取值对本文所考虑的危险品运输问题的影响,本文在θ取不同值时的情况下对模型进行了求解.求解得到θ取不同值时的网络总风险见表2.

表2 θ取不同值时的网络总风险100人
在表2中,当θ≥4时,网络总费用保持不变.为了更加直观的反映表2的信息,将表2反映到折线图中,见图3.
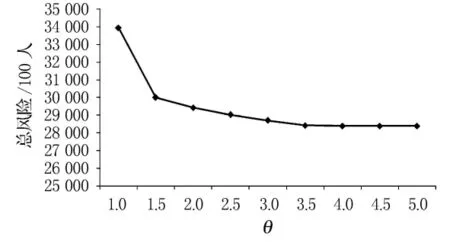
图3 取不同值时的网络总风险
由图3可见,网络的总风险随着θ的取值不同而变化.当θ的取值为(1.0,4.0)时,网络的总风险随着θ的取值增大而减小,且随着θ的增大,总费用减小的速度越来越小.最后当θ的取值超过4.0时,网络总风险不再减小,此时θ对模型失去约束力,相当于不考虑约束式(3)的情形.
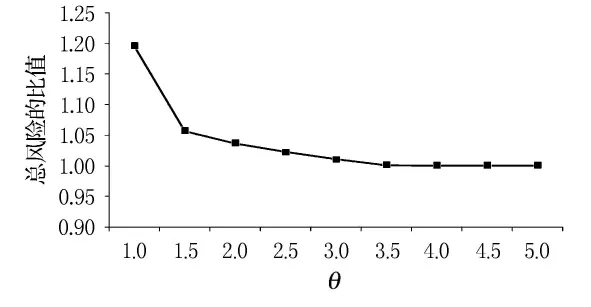
为了突出建立的考虑约束式(3)的路径选择模型较之于不考虑约束式(3)的路径选择模型的优越之处.θ取不同值时的总风险与最小总风险(不考虑不考虑约束式(3)时的总风险)的比值见图4.
由图4可见,在θ的取值从1.0增加到1.5的过程中,总风险相对于最小总风险的比值从1.2减小到1.06,在θ的取值从1.5增加到4.0的过程中,总风险相对于最小总风险的比值却仅从1.06减小到1.从而可以看出当θ的取值大于1.5时,总风险的减小速度是很慢的,从而导致运输者总出行时间的较大幅度的增加,却只能获得较小幅度的总风险的减小.这对于社会总效率来说显然是不可取的.所以政府在做决策时,取θ为1.5或略小于1.5的值是比较合适的,这样既能有效的减小网络的总风险,也能获得政府与运输者效益之间的一个权衡,既有利于政府,运输者的利益损失也不太大.
5 结束语
在定义危险品路段风险的基础上,建立了由政府集中管理情况的危险品运输网络优化模型,模型以网络中的总风险最小为目标函数,并约束运输者的总出行时间不超过运输者在无政府状况下按UE原则选择路径时的总出行时间的θ倍.针对一个简单的算例分析了θ取不同值时网络中的总风险的变化情况.在一定范围内,网络中的总风险随着θ的增大而减小,且减小的速度越来越小,当θ超过一定值时网络中的总风险不再变化.最后,针对算例分析了政府在做决策时的比较合适的θ取值.虽然这个算例不具有一般性,但是针对不同的实际情况,本文所建立的模型和采用的算法仍能为政府的决策提供有价值的参考方案.
[1]ERKUT E,VERTER V.Modeling of transport risk for hazardous materials[J].Operations Research,1998,46(5):625-642.
[2]ERKUT E,GZARA F.Solving the hazmat transport network design problem[J].Computers & Operations Research,2008,35:2234-2247.
[3]VERTER V,KARA B Y.A path-based approach for hazmat transport network design[J].Management Science,2008,54(1):29-40.
[4]KAZANTZI V,KAZANTZIS N,GEROGIANNIS V.Risk informed optimization of a hazardous material multi-periodic transportation model[J].Journal of Loss Prevention in the Process Industries,2011(24):767-773.
[5]魏 航.时变条件下有害物品运输的路径选择研究[D].成都:西南交通大学,2006.
[6]邵春福.交通规划原理[M].北京:中国铁道出版社,2004.
[7]陈 玉.城市道路阻抗函数模型研究[D].西安:长安大学,2008.
[8]李 丹.粒子群优化算法及其应用研究[D].沈阳:东北大学,2006.
[9]陈 曦.粒子群优化算法的改进及在动态交通分配问题中的应用[D].长沙:长沙理工大学,2006.

