考虑滑移效应的三塔结合梁斜拉桥桥面板有效宽度分析*
刘沐宇 刘 洋 袁卫国
(武汉理工大学道路桥梁与结构工程湖北省重点实验室 武汉 430070)
0 引 言
钢-混凝土结合梁斜拉桥以其自重轻、刚度大、抗震性能好等优点,近年来被广泛地应用于大跨径桥梁建设中.结合梁斜拉桥采用双钢主梁形式,斜拉索锚固在两侧的钢主梁上.索力的水平分量以集中力的形式不连续作用于主梁,造成锚固点附近局部应力较大,桥面板中的应力主要集中在钢主梁两侧的有限宽度内.而目前结合梁斜拉桥桥面板有效宽度计算理论实现难度大,现有规范也不完善,导致结合梁斜拉桥桥面板有效宽度分布计算困难,因此,开展结合梁斜拉桥桥面板有效宽度的研究工作,为桥梁结构设计计算提供参考依据是非常必要的.
目前学者们对结合梁斜拉桥桥面板有效宽度的研究主要基于受弯状态下,而结合梁斜拉桥处于压弯状态,仅在受弯状态下进行分析尚不足以准确反映其力学特性[1].同时,现有文献中,钢主梁与混凝土桥面板间一般均视为完全抗剪连接,不考虑滑移[2-3];部分桥梁根据规范要求,除负弯矩区需采用完全抗剪连接外,正弯矩区可根据实际情况和施工方便,采用部分抗剪连接[4-6].但即便是完全抗剪连接情况下,实际中也很难保证钢主梁与混凝土桥面板之间不产生滑移,而这种滑移效应对桥面板中的应力分布影响较大,容易造成桥面板有效宽度计算值不准确.因此,本文以武汉二七长江大桥为工程背景,在压弯状态下,考虑钢主梁与桥面板间的滑移影响,对结合梁斜拉桥桥面板有效宽度进行空间有限元分析,分析结合梁斜拉桥在恒载、正常运营状态下桥面板的应力分布情况,研究抗剪连接程度对桥面板有效宽度的影响,为结合梁斜拉桥设计和施工提供参考.
1 桥面板有效宽度空间有限元分析
1.1 工程背景
武汉二七长江大桥采用3塔双索面钢-混凝土结合梁斜拉桥,主桥长1 732m,跨径组成为90 m+160m+616m+616m+160m+90m,见图1.钢主梁采用工字型,位于桥面两侧间距为30.5 m,梁高2.935m,斜拉索锚固间距为13.5m,每个索距设三道横梁,横梁间距为4.5m.在桥中心线处设置小纵梁,混凝土桥面板板厚为0.26m,采用直径×长度=22mm×200mm螺栓与钢主梁连接.主桥采用半漂浮体系,边塔处设置竖向支撑,中塔处为固定铰接体系.

图1 二七路长江大桥立面布置图(单位:m)
1.2 节段分析模型
建立全桥板壳模型进行桥面板有效宽度有限元分析,难度较大且无法实现.因此,根据结合梁斜拉桥的特点,选取典型节段模拟分析[7],分别为主跨跨中、主跨1/4、主跨3/8、边跨跨中、边塔塔根、中塔塔根处.为细致研究结合梁斜拉桥主梁在压弯状态下的工作状况,沿桥纵向截取5段索距长度,分别建立节段有限元模型.钢主梁、横梁和小纵梁均采用shell63单元,混凝土桥面板采用solid45单元,预应力筋采用link8单元,运用降温法模拟.同时,考虑钢主梁与桥面板间的滑移影响[8-9],用弹簧combin39单 元 来 模 拟 栓 钉 的 连 接作用.只考虑沿桥纵向的滑移,忽略横向的位移和混凝土板的掀起,即耦合对应节点的x、y方向,在z方向建立一个非线性弹簧单元,见图2.
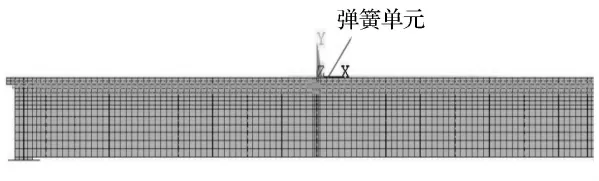
图2 钢主梁与混凝土桥面板间的弹簧单元
主跨跨中空间有限元节段模型见图3,共划分174 786个实体单元,182 676个壳单元,5 423个弹簧单元.汽车荷载采用等效均布荷载模拟,通过表面效应单元将力施加在对应轮载位置处.在节段模型的边界处找出形心点作为主节点,形成刚域,从全桥ANSYS模型中提取各节段边界上节点的位移,然后施加在对应主节点上.

图3 主跨跨中节段有限元模型
2 典型节段处桥面板有效宽度分析
考虑钢与混凝土桥面板间的滑移影响,对上述节段模型在恒载、正常运营状态下(恒+活+温度)2种工况进行计算,明确桥面板上应力的分布情况,进而根据公式计算出桥面板的有效宽度和有效宽度系数[10-11].由于桥面板厚度较薄,应力沿厚度方向视为均匀分布,取上表面应力分析[12].
1)在恒载作用下桥面板中正应力分布情况.计算结果见表1,根据计算结果绘制桥面板正应力分布图,见图4.根据文献[3],各截面桥面板的有效宽度和有效宽度系数分别按式(1),(2)进行计算,计算结果见表2.
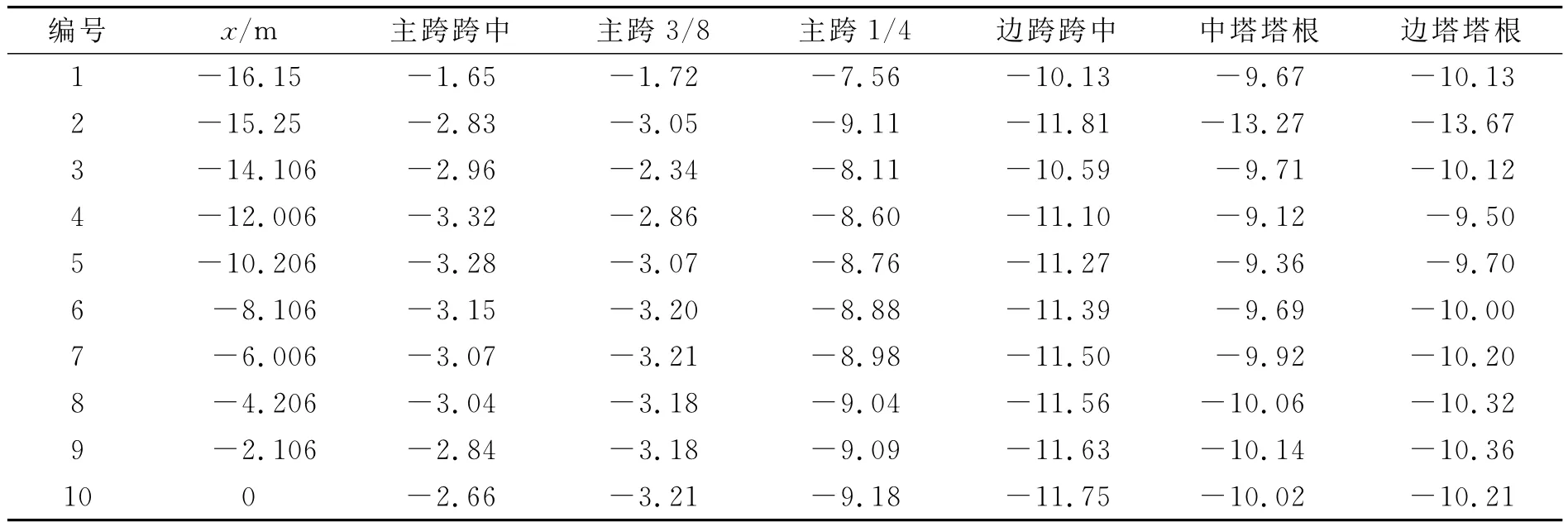
表1 恒载作用下各控制截面半幅桥面板正应力值 MPa

图4 恒载作用下各控制截面半幅桥面板正应力分布图
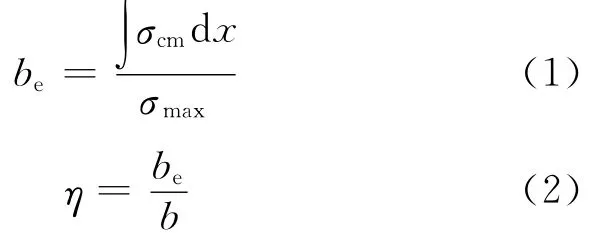
根据“无限细分”和“无限求和”的思想和有限元的计算结果,式(1)可按下式近似计算
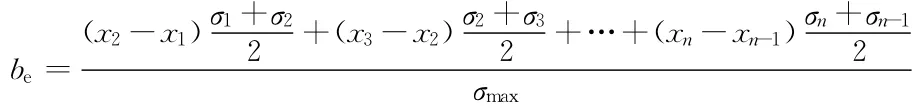
式中:be为桥面板的有效宽度;b为桥面板的实际宽度;σcm为桥面板中正应力;σmax为桥面板中最大正应力;η为桥面板有效宽度滞系数;σn-1和σn分别为第(n-1)个单元计算截面上2个节点的正应力;xn-1和xn为第(n-1)个单元计算截面位置上2个节点距桥面中心的横向坐标值.
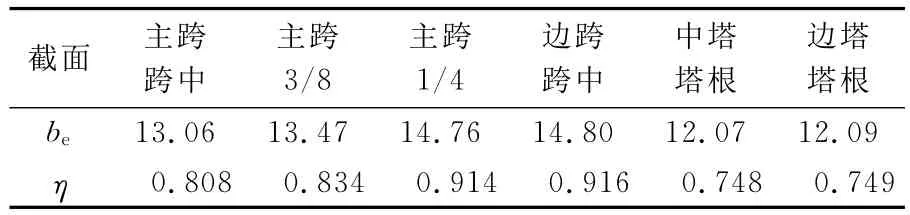
表2 各控制截面半幅桥面板有效宽度和有效宽度系数
从表1,2可以看出,结合梁斜拉桥桥面板有效宽度分布不均匀,应力分布图4也说明了这一点;桥面板上的应力沿横向分布不均匀,在钢主梁处应力值较大,桥梁中心线附近应力分布较均匀.有效宽度系数η取值在0.748~0.916之间.中塔塔根和边塔塔根处桥面板的有效宽度和有效宽度系数最小,说明塔根处桥面板有效宽度分布最不均匀.
2)正常运营状态下主跨跨中桥面板正应力分布情况,计算结果见图5.由图5可见,斜拉索在钢主梁上的水平力是造成结合梁斜拉桥桥面板应力突变的最主要原因,在靠近斜拉索锚固点附近混凝土桥面板上的局部应力值较大,远离斜拉索桥面板上应力值趋于均匀.
3 抗剪连接程度对桥面板有效宽度的影响
结合梁在设计时,正弯矩区为了方便施工和经济效益,钢和混凝土板之间往往采用部分抗剪连接,抗剪连接程度对混凝土板中的应力分布有较大影响,如不考虑该因素会造成混凝土板的有效宽度计算不准确[13-15].结合梁斜拉桥主跨跨中桥面板中有可能出现拉应力,且其应力较其他位置更容易出现重分布现象.因此,本文选择结合梁斜拉桥主跨跨中处节段,改变抗剪连接程度数值,比较分析混凝土桥面板中应力分布情况,明确抗剪连接程度对桥面板有效宽度的影响,确定最佳的抗剪连接程度数值,计算结果见图6.

图5 正常运营状态下主跨跨中桥面板正应力分布z-为距主跨跨中的距离,在z=5.4m处有一根斜拉索.
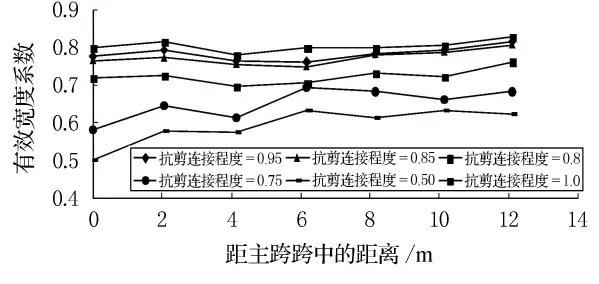
图6 不同抗剪连接程度下主跨跨中附近桥面板有效宽度系数分布
由图6可见,抗剪连接程度对桥面板中应力分布有较大影响,在计算有效宽度时,考虑钢主梁与混凝土桥面板间的滑移可使计算结果更加准确.采用部分抗剪连接可以满足结合梁受力的要求,但如抗剪连接程度过低,钢与混凝土间滑移较大,严重影响结合梁的极限承载力,分析图6,结合梁的最佳抗剪连接程度控制在0.80~1.0之间.
4 结 论
1)结合梁斜拉桥桥面板有效宽度分布不均匀,中塔塔根和边塔塔根处桥面板的有效宽度和有效宽度系数最小.
2)斜拉索的水平分力是造成结合梁斜拉桥桥面板应力突变的主要原因,在拉索集中作用点附近,桥面板中应力分布较不均匀,出现应力局部过大的现象,靠近桥面中心线处桥面板中的应力趋于均匀.
3)由表2计算的各控制截面的有效宽度分布值可知,结合梁斜拉桥在恒载作用下,桥面板有效宽度可取全截面宽度的0.748~0.916倍计算.
4)钢主梁与混凝土桥面板间的抗剪连接程度对桥面板中应力分布造成较大影响,考虑钢与混凝土的滑移,可提高桥面板有效宽度计算的准确度.采用部分抗剪连接可以满足结合梁受力的要求,其最佳抗剪连接程度在0.80~1.0之间.
[1]颜 娟,黄才良,张 哲.双主梁式斜拉桥主梁有效宽度[J].长安大学学报:自然科学版,2003,23(1):46-48.
[2]芶 洁,朱 浩.结合梁斜拉桥剪力滞问题的研究[J].四川建筑,2009,29(1):134-136.
[3]聂建国,李法雄,樊健生.组合梁斜拉桥桥面有效宽度分析[J].哈尔滨工业大学学报,2007,39(2):718-724.
[4]中华人民共和国建设部.GB 50017-2003钢结构设计规范[S].北京:中国计划出版社,2003.
[5]Commission of the European Communities.Eurocode 4:Design of composite steel and concrete structures[S].Commission of the European Communities,1992.
[6]Maunsell Ltd.BS 5400steel concrete and composite bridges,Part3[S].London:British Standars Institution,1982.
[7]周绪红,狄 谨,戴公连.大跨径预应力混凝土斜拉桥主梁节段模型的研究[J].土木工程学报,2005,38(3):59-63.
[8]王文炜,翁昌年,万 水,等.考虑滑移的钢-混凝土组合梁有限单元法[J].东南大学学报:自然科学版,2007,37(2):206-211.
[9]SALARI M R,SPACONE E.Analysis of steel-con
crete composite frames with bond-slip[J].Journal of Structural Engineering,2001,127(11):1243-1250.[10]AMADIO C,FRAGIAXOMO M.Effective width evaluation for steel-concrete compositebeams[J].Fournal of Constructional Steel Research,2002,58:373-388.
[11]AMADIO C,FEDRIGO C,FRAGIACOMO M,et al.Experimental evaluation of effective widthin steel-concrete composite beams[J].J.Constr.Steel Res.,2004,60:199-220.
[12]AMADIO C,FRAGIACOMO M.Effective width evaluation for steel-concrete composite beams[J].J.Constr.Steel Res.,2002,58(3):378-388.
[13]樊健生,聂建国.部分抗剪连接组合梁承载力的计
算[J].哈尔滨工业大学学报,2005,37(S):230-233.[14]韦芳芳,吕志涛,孙文彬.部分剪力连接钢-混凝土组
合梁的非线性有限元分析[J].工业建筑,2003,33(9):78-80.
[15]LOH Y H,UY B,BRADFORD M A.The effects of partial connection in the hogging moment regions of composite beams part I-experimental study[J].J.Constr.Steel Res.,2004,60:897-906.

