齿轮副整体误差及其获取方法

石照耀，康 焱

以黄潼年先生为主的我国科技工作者于1970年在世界上首创了齿轮整体误差测量技术[1-2]，这项被誉为新中国机械工程领域首项原创性的成果，在《中国科学》[3]得到全面介绍．经过后续20多年的发展，齿轮整体误差测量技术已成为系统的齿轮整体误差理论[4]．它主要包括 3方面内容：齿轮整体误差概念及其分析方法、齿轮整体误差的获取方法和齿轮整体误差应用[5-7]．我国曾生产了 1,000多台各式齿轮整体误差测量仪器，并出口到一系列国家，其中锥齿轮整体误差测量技术的专利于 1989年卖给了德国的Klinglnberg公司，实现了新中国机械工程领域的首项高技术出口[8]．目前仍有200多台齿轮整体误差测量仪器应用在生产现场[9]．但很遗憾，近10多年来齿轮整体误差测量技术未得到应有的发展．

齿轮整体误差通过特殊跳牙标准件与齿轮的啮合测量获取，得到的是单个齿轮的误差信息，其关键之处是使标准件与被测齿轮的重合度ε＜1．从技术上讲，齿轮整体误差具有 3个鲜明的特点[7]：一是反映了齿轮的全部误差信息；其次是形象而精确地揭示了齿轮各单项误差的变化规律以及彼此间的消长关系；三是反映了齿轮传动的啮合过程．

实际应用中，齿轮是成对使用的．由于主、从动轮都有误差，实际传动效果是主、从动轮共同作用的结果．由于齿轮副的重合度ε＞1，从常规的齿轮传动误差不能厘清实际齿轮的啮合过程及其与误差相关的各种问题[10]．为此，笔者将单个齿轮的整体误差概念拓展到了齿轮副，提出了齿轮副整体误差(gear pair integrated error，GPIE)的基本概念[11]、数学模型、理论方程、单元曲线和基本算法，给出了具体可行的获取方法，并开发了测量系统．

1 数学模型与单元曲线

1.1 齿轮副整体误差的数学模型

齿轮传动依靠主动轮的轮齿依次推动从动轮的轮齿进行工作，其推动过程通过共轭齿面的交替啮合来实现．如图 1所示[12]，1U和2U是一对渐开螺旋共轭齿面，iM为某一时刻的啮合点，啮合点在空间的轨迹形成啮合线，啮合线是共轭齿面传递位移和力的作用线．图 1 中，σ(O2，n，τ，η)为与基架固连的基础标架，其中，O2为从动轮固定轴线的对称中心点，n为齿轮副啮合线上的单位矢量，η为从动轮固定轴线的单位矢量，τ 与n和η一块组成右旋直角坐标系．

由于制造与安装等方面的原因，实际齿轮的齿面总是存在各种偏差，而且各齿面间的位置关系也可能存在偏差．设 Σ1和 Σ2分别为共轭齿面 U1和 U2对应的含有偏差的实际齿面，Q1和 Q2为理论啮合点 Mi在实际齿面 Σ1和 Σ2上对应的实际接触点．一般而言，Q1、Q2和 Mi在空间的位置很接近，为了表示方便，这里放大了它们之间的相对距离．

在啮合点iM 处建立活动标架σM(iM ，ni，τi，ηi)，ni为共轭齿面的单位法矢量，τi和ηi为iM 点处切平面上互相垂直的 2个单位矢量．由啮合线的性质可知：iM必然落在n轴线上的理论啮合线范围内，故

在活动标架σM中，设

设Ei为从动轮的一个补偿位移矢量，且满足

利用矢量关系，式(3)可变为

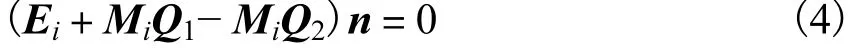
由式(4)可知，只要再给从动轮一个补偿位移 Ei时，实际齿面 Σ1和 Σ2上的实际接触点1Q和2Q就会在理论啮合点iM 处啮合．可见，矢量 MiQ1和 MiQ2之差在 ni方向的分量使得实际齿面和理论共轭齿面在iM 点处沿着啮合线方向产生大小为 Δi的偏差，使其偏离了预定的运动规律．这种真实值和理论值之间的偏差正是齿轮副在该时刻的运动误差．

图1 齿轮副整体误差的数学模型Fig.1 Mathematical model of the GPIE

从偏差产生的原因来讲，MiQ1是主动轮在iM 点的原始偏差矢量，MiQ2是从动轮在 Mi点的原始偏差矢量，分别由主从动轮的各单项偏差(如基圆齿距偏差、齿廓偏差等)在该点的综合作用引起．

从上述数学模型可知，在主从动轮的原始误差矢量中，只有沿啮合线 n方向的分量最终引起齿轮副的运动误差，从而影响传动质量．

齿轮副整体误差把主、从动轮所有共轭齿面上的误差视为一个整体，并把各共轭齿面上各接触点的误差按实际啮合顺序统一在啮合线(或啮合线族)上而形成的一种齿轮副误差集合．从而把主、从动轮的几何量误差和齿轮副传动时的运动量误差合为一体，把齿轮误差和齿轮传动时的传动特性联系在一起，组成一个完整的集成体．

图1中iM点的齿轮副整体误差iF可以表示为

式中MiQ1·n和 MiQ2·n分别表示主从动轮的各单项偏差在啮合线方向综合作用的效果．

齿轮整体误差反映了齿轮各单项偏差在啮合线方向的综合作用[13]，设 fi1、fi2分别为主从动轮在接触点 Mi的齿轮整体误差，则有

由式(5)～式(7)可得，在任意的接触点iM 处齿轮副整体误差和主从动轮整体误差存在的关系为

在齿轮整体误差理论中，规定齿廓误差曲线上的“＋”偏差代表齿面凸起的误差[3]，式(8)中，把使从动轮滞后的齿轮副整体误差规定为“－”．

1.2 单元齿轮副整体误差曲线

把齿轮副整体误差用误差曲线[12]的形式记录下来即可得到齿轮副整体误差曲线．由齿轮的结构特点和齿轮啮合原理可知，相邻两啮合齿对的齿轮副整体误差曲线相对独立，单对齿的齿轮副整体误差曲线是齿轮副整体误差曲线的基本组成单元，因此，把单对齿的齿轮副整体误差曲线称为单元齿轮副整体误差曲线．

单元齿轮副整体误差曲线由3部分组成，如图2所示，依据啮合顺序依次是：、和，描述了一个啮合齿对的完整啮合过程．其中：段和段分别是从动轮和主动轮的顶刃啮合阶段，段是正常渐开线啮合阶段．理论单元齿轮副整体误差曲线方程可表示[11,14]为

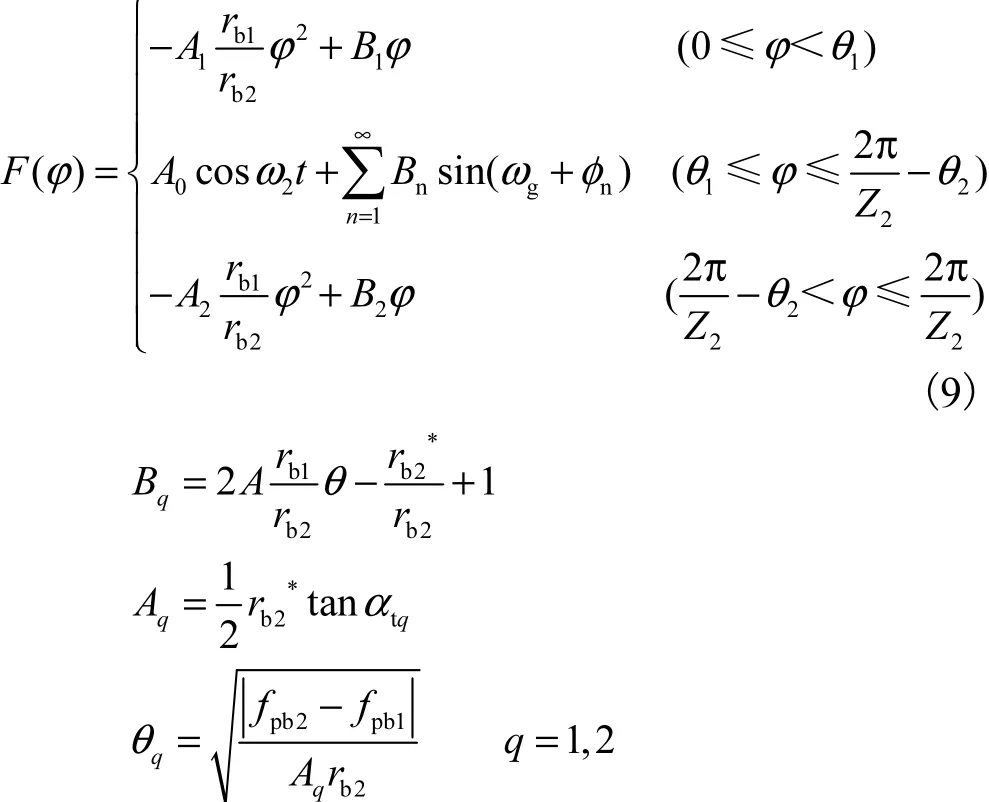
式中：rb1*和 rb2*分别为主、从动轮的实际基圆半径；rb1和rb2分别为主、从动轮的理论基圆半径；αt1和αt2分别为主、从动轮的齿顶压力角；Z2为从动轮齿数；A0为长周期误差的幅值；ω2为从动轮回转角频率；Bn为短周期误差的幅值；ωg为啮合角频率；φn为短周期误差的相位角；fpb1、fpb2分别为主、从基圆齿距偏差．

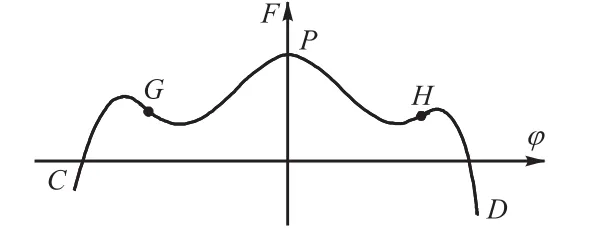
图2 单元齿轮副整体误差曲线Fig.2 Unit GPIE curve

2 齿轮副整体误差曲线的获取方法

由式(8)可知，齿轮副整体误差可采用间接测量法获得．首先利用齿轮整体误差仪器 CZ450测量主从动轮的齿轮整体误差，然后合成得到齿轮副整体误差曲线．间接法获取齿轮副整体误差时，分为2步．

1)单元齿轮副整体误差曲线的获取

以平行轴直齿轮副为例[15]．图 3表示了平行轴渐开线直齿轮副的几何特点，主动轮O1和从动轮O2均为有误差的实际齿轮，绕着各自的固定轴线旋转．齿轮副的整个啮合过程都在接触面上进行，图 3中的中间图表示接触面的投影图，其中，用粗实线组成的矩形为啮合域，接触面上间隔为基节bP的直线带表示齿轮副各啮合齿对的接触线．在齿轮啮合过程中，对于主动轮齿面的任意一个接触点，从动轮对应的共轭齿廓上有且只有一点与之对应．

主动轮上的轮齿是从齿根域附近的实际工作部分起点 R1开始接触，最后从齿顶 T1脱离接触；从动轮则相反，从齿顶 T2开始接触，最后从齿根域附近的有效工作部分起点R2脱离接触．当主动轮转过Δθ1时，从动轮将会转过相应的 Δθ2(Δθ1Δ θ2= i12，i12为传动比)，这时主动轮和从动轮上的接触点又组成共轭对，它们彼此的齿轮整体误差共同构成该时刻的等效齿轮副整体误差．

在接触面上，建立图 3所示的直角坐标系x0O0y0，称为接触面坐标系，其中，x0轴为接触线的对称线，用来表示接触点距原点的横向位置，纵坐标y0用来表示接触点的轴向位置．在接触面坐标系中，坐标对与啮合过程中的接触点一一对应．

在接触面坐标系中，任意接触点(x,y)的齿轮副整体误差可以表示为

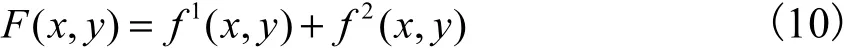
式中： (,)Fxy为齿轮副在接触点(,)xy处的齿轮副整体误差；1(,)fxy、2(,)f xy分别为主、从动轮在接触点(,)xy处的齿轮整体误差．

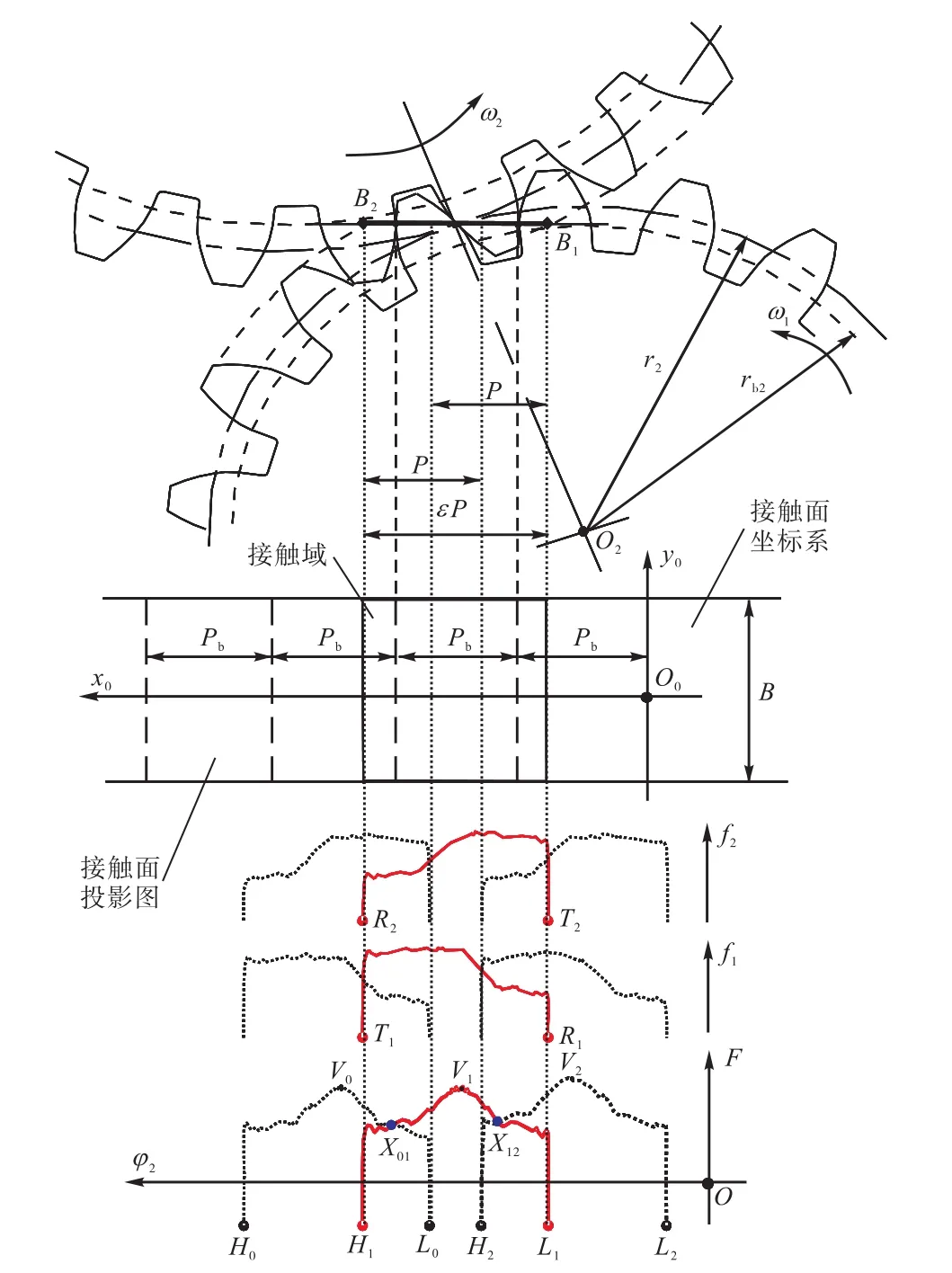
图3 单元齿轮副整体误差曲线的算法原理Fig.3 Basic arithmetic about unit GPIE curves

2) 完整啮合周期上的齿轮副整体误差曲线的获取

用相同的方法得到所有啮合齿对的单元齿轮副整体误差曲线，最后根据它们实际的啮合顺序在接触面坐标系中统一在一起，就得到完整啮合周期上的齿轮副整体误差曲线．

在完整啮合周期中，主、从动轮的转数分别为：N1=z2z1, z2，N2=z1z1, z2，其中， z1,z2为 z1和 z2的最大公因数．

这种移除其他齿的研究方法，可以在不考虑其他相邻齿对影响下计算出啮合齿对的齿轮副整体误差，避开了实际齿轮啮合过程中双齿啮合给测量带来的不便．它可以应用于任何类型的齿轮，不仅仅局限于渐开线齿形，可以应用于平行轴齿轮副，也可以应用于交错轴齿轮副．

3 测量系统及测量实例

以前述齿轮副整体误差获取方法为理论基础，采用面向对象的程序设计方法，在齿轮整体误差测量仪CZ450的硬件基础上开发了齿轮副整体误差测量系统．主界面是典型的Windows应用软件风格，包含菜单栏、工具栏、状态栏和客户区窗口等．

图4为齿轮副整体误差测量系统的总体架构，分为3个模块：硬件和数据采集模块、齿轮整体误差测量和存储模块以及齿轮副整体误差计算和存储模块．其中，硬件和数据采集模块是以齿轮整体误差测量仪CZ450的硬件结构为基础，重新设计和开发测量误差数据采集单元，测量数据采集流程如图5所示；齿轮为105．图6所示为获得的齿轮副整体误差曲线及其幅频曲线．整体误差测量和存储模块主要由数据处理算法单元、误差数据存储单元和误差数据输出显示单元组成[16]．数据处理算法单元采用最新的齿轮精度标准和规范来进行齿轮各项误差数据的处理．

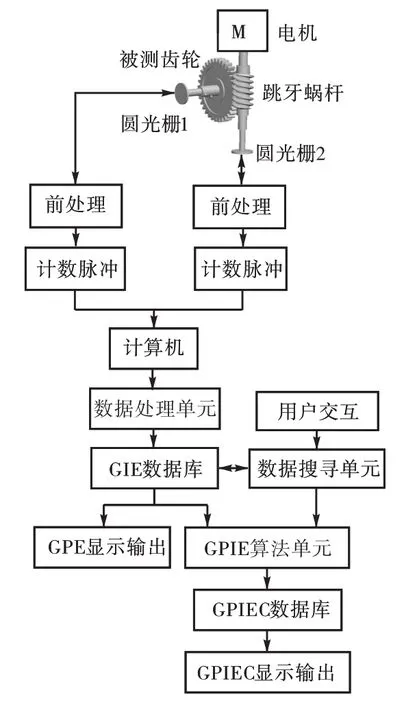
图4 测量系统总体架构Fig.4 Architecture of the measuring system

表1 齿轮参数Tab.1 Gear’s parameters

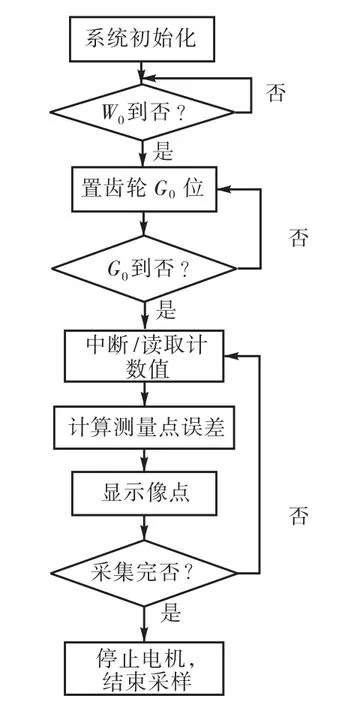
图5 测量数据采集流程Fig.5 Flow chart of measurement data

齿轮副整体误差计算和存储模块由用户交互单元、数据搜寻单元、GPIE算法单元、GPIE数据库和输出显示单元 5部分组成．其中，GPIE算法单元为整个测量系统的关键模块，涉及的关键问题有3个．

(1) 确定主从动轮实际工作部分及其对应的误差数据，并按照实际啮合顺序重新排序．其中，主动轮是从齿根域附近的实际工作部分起点进入啮合，到齿顶处终止啮合，而从动轮则是从齿顶开始，到实际工作部分起点处结束．

(2) 主从动轮对应共轭点处齿轮整体误差的二次插值计算．根据传动比，搜寻和计算主从动轮一一对应的共轭点及其对应的误差值，如果前面测量得到的误差数据中没有对应共轭点的误差值，则需要根据前后相邻 2点的误差值来插值计算．由于 1个轮齿上的数据采集点比较密集，一般为 100～130个采集点，因此这里选择线性插值．

(3) 依据单元齿轮副整体误差曲线的基本算法合成各共轭点处的齿轮副整体误差值，并进行验证．

另外，整个测量系统具有统一的系统流程管理服务层，为实现测量系统的各功能提供管理服务，主要包括用户管理、数据规划、算法管理和各类测量数据、误差数据的数据库管理．

在齿轮副整体误差测量系统中，对表1所示的齿轮副进行测量．测量中，每个齿面上的数据采集点数

图6 齿轮副整体误差曲线及其幅频曲线Fig.6 GPIE curve and the spectrum of the gear pair as shown in Tab.1

4 齿轮副整体误差的优点

(1) 齿轮副整体误差曲线的外包络线就是空载时的传动误差(transmission error，TE)曲线，如图7所示．相对于传动误差，齿轮副整体误差包含的误差信息更全面，它既可以评定齿轮副的传动质量，又可分析误差来源于哪一对或哪几对齿面，还可以研究在双啮区时，同时参与啮合的2对轮齿的误差是如何相互影响传动质量，从而为更好地控制齿轮副的传动质量，为调整齿轮工艺和改进齿轮设计提供了依据．

(2) 齿轮副整体误差结合了主从动轮的整体误差，不仅反映了啮合过程中主从动轮误差相互作用的结果，更重要的是反映了主从动轮误差相互作用的形式和过程，尤其揭示了啮合齿对的交替过程[17]．

(3) 齿轮副整体误差把主从动齿轮的几何误差与齿轮副的运动误差紧密地结合起来，能揭示有误差的齿轮的实际啮合过程和齿轮几何误差对传动质量的影响[18]．

(4) 利用齿轮副整体误差，可以研究齿轮承载后的误差变化趋势；与动力学结合，能研究齿轮冲击，进而预报齿轮的动态特性，如振动和噪声[19]．

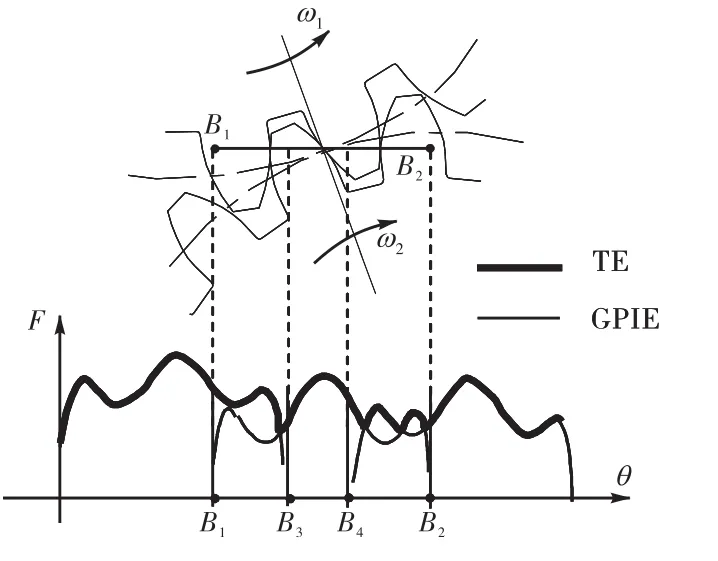
图7 齿轮副整体误差曲线和传动误差曲线的比较Fig.7 Comparison between the GPIE curve and the TE curve

5 结 语

齿轮副整体误差把主、从动轮所有共轭齿面上的误差视为一个整体，提供了共轭齿面上完整的误差信息，克服了传动误差在研究问题中的局限性，既可进行齿轮啮合过程的研究和传动质量的评定，又可用于误差溯源，进行齿轮工艺误差的分析．齿轮副整体误差获取方法，以齿轮整体误差测量技术为基础，既解决了传动误差测量中存在的问题，又发展了我国首创的齿轮整体误差理论．开发的齿轮整体误差测量系统可以提供齿轮副完整啮合周期上的误差数据和完整的误差信息．

因此，对齿轮副整体误差进行剖析，研究与之相关的其他齿轮问题，能够得出一系列从前难以得到的结果，为齿轮的选配、控制齿轮传动质量、降低齿轮振动和噪声提供了一种新途径．

［1］ 一机部军管会(70)一机军技字223号：单啮仪总结、交流、推广会通知[Z].

The Military Management Department of the First Mechanical Department(70)：The Summing，Communicating and Spreading Meeting Notice of the Gear Single-Flank Meshing Tester[Z](in Chinese).

［2］ 我国齿轮测量技术达到世界水平[N]. 人民日报，1978-03-15(2).

The gear measurement technology in China reached world level[N]. Pelple’s Daily，1978-03-15(2)(in Chinese).

［3］ 黄潼年. 齿轮动态全误差曲线及其测量方法[J]. 中国科学，1973，17(4)：434-453.

Huang Tongnian. Gear dynamic composite error and its measurement method[J]. Science in China，1973，17(4)：434-453(in Chinese).

［4］ 石照耀，费业泰，谢华锟. 齿轮测量技术 100年：回顾与展望[J]. 中国工程科学，2003，5(9)：13-17.

Shi Zhaoyao，Fei Yetai，Xie Huakun. 100 years of gear measurement technology：Review and prospect[J]. Engineering Science，2003，5(9)：13-17(in Chinese).

［5］ Huang T N. The development of gear integrated error measurement in China[C]//Proceedings of Inter Conf of Gearing. Zhengzhou，China，1989：25-31.

［6］ 成都工具研究所，北京量具刃具厂. 齿轮动态全误差测量新技术[M]. 北京：国防工业出版社，1977.

Chengdu Tool Research Institute，Beijing Measuring and Cutting Tool Company. The New Measurement Technology of the Dynamic Gear Integrated Error[M]. Beijing：National Defence Industry Press，1977(in Chinese).

［7］ 姚福生，石照耀，张兆龙，等. 中国特色的齿轮测量：齿轮整体误差测量技术[G]//中国工程院. 中国科学技术前沿. 上海：上海教育出版社，1997：398-413.

Yao Fusheng，Shi Zhaoyao，Zhang Zhaolong，et al. A new kind of gear measurement technology developed in China：The gear integrated error measurement technology[G]//Chinese Academy of Engineering. Frontier Science and Technology in China. Shanghai：Shanghai Education Publishing House，1997：398-416(in Chinese).

［8］ 石照耀，张兆龙，谢华锟. 齿轮整体误差测量技术的发展与应用前景[J]. 工具展望，1999(2)：14-17.

Shi Zhaoyao，Zhang Zhaolong，Xie Huakun. The development and application of the measuring technology of the gear integrated error[J]. Tool Engineering，1999(2)：14-17(in Chinese).

［9］ 石照耀. 齿轮量仪[G]//2010中国齿轮工业年鉴. 北京：北京理工大学出版社，2010：36-39.

Shi Zhaoyao. Gear measuring tools[G]//Gear 2010 China Gears Industry Yearbook. Beijing：Beijing Institute of Technology Press，2010：36-39(in Chinese).

［10］ Smith J D. The uses and limitations of transmission error[J]. Gear Technology，1988，5：34-39.

［11］ 石照耀. 齿轮整体误差与齿轮传动噪声关系研究[D].西安：陕西机械学院机械系，1988.

SHI Zhaoyao. The Research on the Relation of the Gear Integrated Error and Gear Noise[D]. Xi’an：Department of Mechanical Engineering，Shaanxi Institute of Mechanical，1988(in Chinese).

［12］ Litvin F L，Fuentes A. Gear Geometry and Applied Theory[M]. Cambridge：Cambridge University Press，2004.

［13］ 成都工具研究所. 齿轮整体误差曲线图册[M]. 北京：国防工业出版社，1982.

Chengdu Tool Research Institute. The Curve of the Gear Integrated Error[M]. Beijing：National Defence Industry Press，1982(in Chinese).

［14］ 柏永新. 齿轮精度与综合检验[M]. 上海：上海科学技术出版社，1986.

Bai Yongxin. Gear Metrology and Inspection[M].Shanghai：Shanghai Science and Technology Press，1986(in Chinese).

［15］ Mark W D. Analysis of the vibratory excitation of gear systems：Basic theory[J]. Journal Acoustical Society of America，1978，63(5)：1409-1430.

［16］ 石照耀，唐为军. 齿轮整体误差测量系统的重构[J].机械传动，2007，31(1)：1-3.

Shi Zhaoyao，Tang Weijun. Reconstruction of the gear integrated error measuring system[J]. Journal of Mechanical Transmission，2007，31(1)：1-3(in Chinese).

［17］ 石照耀，张 旭. 齿轮单面啮合测量技术的发展及其应用[J]. 工具技术，2008，42(3)：10-15.

Shi Zhaoyao，Zhang Xu. The development and application of gear single-flank testing technology[J]. Tool Engineering，2008，42(3)：10-15(in Chinese).

［18］ 柏永新. 齿轮动态整体误差测量新技术的应用[M].北京：国防工业出版社，1982.

Bai Yongxin. The Appliance of the Measuring Technology of the Gear Integrated Error[M]. Beijing：National Defence Industry Press，1982(in Chinese).

［19］ 石照耀，康 焱，林家春. 基于齿轮副整体误差的直齿轮动力学模型及其动态特性[J]. 机械工程学报，2010，46(17)：55-61.

Shi Zhaoyao，Kang Yan，Lin Jiachun. A comprehensive dynamics model and dynamic response analysis of a spur gear pair based on gear pair integrated error[J]. Journal of Mechanical Engineering，2010，46(17)：55-61(in Chinese).