药物代谢动力学软件设计（三室模型）

范景行

（甘肃民族师范学院，甘肃 合作 747000）

药物代谢动力学软件设计（三室模型）

范景行

（甘肃民族师范学院，甘肃 合作 747000）

本文的研究范畴是三室模型线性药物动力学，包括一次静脉推注给药、一次血管外给药、静脉滴注给药3种模型。首先根据模型列出微分方程组，求出方程组的特解方程，然后将参数整合，根据已知数据求出参数值，也就是拟合出一条曲线。拟合曲线使用最小二乘法和Gauss-Newton迭代法求解，针对奇异矩阵导致Gauss-Newton法迭代结果发散的缺点，引进了Levenberg-Marquardt法，针对残差平方和偏重高密度数据点的缺点，引进了权重。所有算法都用C语言实现。

药物代谢动力学；最小二乘法；Gauss-Newton法；Levenberg-Marquardt法

药物代谢动力学（也称药动学、药物动力学、药代动力学，PK）是研究药物及其代谢物在体内吸收、分布、转化和排泄过程中，随着时间不同，不断进行运动变化规律的科学。药物代谢动力学研究的对象是人体，对患病的机体以及正常人体用药后，观察药物在体内的变化过程。根据该科学可对患者提供安全、有效的治疗方案，包括给药途径、用药剂型、用法、用量、给药间隔等，实现给药方案个体化；可重新审查给药计划，对不良反应做出解释；可按计划对正在进行血液、腹膜透析的患者给药，预防中毒。根据该科学可及时地进行血药浓度的监测，广泛地收集药学情报，为临床提供科学的给药方案，进一步提高疗效，减少药物的不良反应。所以该学科所肩负的任务非常重要，其研究是采用数学手段（如用图像、公式、参数等方法）来描述药物在体内运动过程中的规律，因而可为用药方案的设计提供重要的参考依据。

药物代谢动力学从数学的角度可分为两类：线性药物代谢动力学和非线性药物代谢动力学。在线性药物代谢动力学中，药物代谢动力学参数如半衰期与剂量无关；而在非线性药物代谢动力学中，药物代谢动力学参数随剂量（或体内药物浓度）而变化，如半衰期与剂量有关。本文所讨论的内容准确地说属于线性药物代谢动力学范畴，并以三室模型为研究对象，对一次静脉推注给药、一次血管外给药、静脉滴注给药3种常见的给药方式做详细介绍。

1 模型的建立

1.1 一次静脉推注给药的三室模型

药物的三室模型可以这样设想：假定药物进入中心室后，逐渐向两个周边室转运，在中央室与周边室之间药物进行着可逆的运动，药物在中央室按一级过程消除[1]，其体内过程模型见图1。

图1 一次静脉推注给药的三室模型

图1 显示：X0为静脉注射给药剂量；XC为中央室的药量；XP和XB为周边室的药量；k12和k21为中央室与浅外室之间的运转速度常数；k13和k31为中央室与深外室之间的运转速度常数；k10为药物从中央室消除的一级速度常数；VC、VP、VB分别为中央室、浅外室、深外室的表观分布容积。

假如药物的转运过程均服从一级速度过程，即药物的转运速度与该室药物浓度（或药量）成正比，则各室药物的转运可用下列微分方程组定量描述[2]。

当t=0时，注射的药物全部存放于中心室内，尚未转运至其他各室。所以XC（0）=X0，XP（0）=XB（0）=0，这就是以上方程组的初始条件。

因为实际测量的数据普遍都以中央室为主，所以我们只讨论中央室的血药浓度与时间的关系。设C为中央室药物浓度，通过求解化简可得需要拟合的数学方程：

1.2 静脉滴注给药的三室模型

设剂量为X0的药物，在τ0这段时间内，以恒速k0=D0/τ0滴入中心室，其体内过程模型[3]见图2。

图2 静脉滴注给药的三室模型

图2 显示：X0为静脉注射给药剂量；XC为中央室的药量；XP和XB为周边室的药量；k12和k21为中央室与浅外室之间的运转速度常数；k13和k31为中央室与深外室之间的运转速度常数；k10为药物从中央室消除的一级速度常数；VC、VP、VB分别为中央室、浅外室、深外室的表观分布容积。

在经过滴注时间t（0≤t≤τ）时，中心室的药量为XC（t），周边室的药量为XP（t）和XB（t）。除滴注是恒速K0之外，如果其余各转运过程服从一级动力学过程，则各室间的药物转运方程为[4]：

当t=0时，XC（0）=XP（0）=XB（0）=0，这就是以上方程组的初始条件。

因为实际测量的数据普遍都以中央室为主，所以我们只讨论中央室的血药浓度与时间的关系。同理可得：

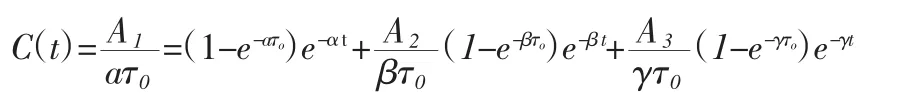
这就是滴注后中心室的药物浓度与时间关系。其中，是从滴注完成时算起。

1.3 一次血管外给药的三室模型

有些药物不能做静脉推注给药时，则采用血管外给药，仅需在静脉推注给药的三室模型中心室前增加一个吸收室，让药物逐渐从吸收室转运至中心室，再转运至两个周边室[5]（见图3）。

图3 一次血管外给药的三室模型

图3 显示：X0为给药剂量；Xa为吸收室药量；XC为中央室的药量；XP和XB为周边室的药量；kа为吸收速度常数；k12和k21为中央室与浅外室之间的运转速度常数；k13和k31为中央室与深外室之间的运转速度常数；k10为药物从中央室消除的一级速度常数；Vа、VC、VP、VB分别为吸收室、中央室、浅外室、深外室的表观分布容积。

假定吸收过程仍是一级过程，则各室间的药物运转可用下列方程表示[6]：

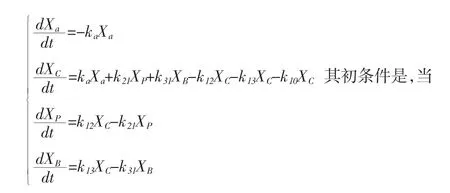
因为实际测量的数据普遍都以中央室为主，所以我们只讨论中央室的血药浓度与时间的关系。同理可得：

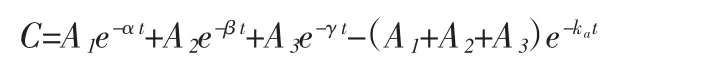
2 模型的求解算法

Gauss-Newton 算法步骤归纳如下[7，8]：

（1）取初始近似值A0，允许误差ε；

（2）计算 F（XY，A0），DF（X，Y，A0），DF（X，Y，A0）T；

（3）解线性方程组：

得△A；

（4）以△ A修正 A0，即计算：A=A0+△ A；

（5）若|△ A|＞ε，则 A0=A，即将 A 作为初值 A0，重复步骤（2）、（3）、（4），直至|△ A|＜ε。

由于Gauss-Newton法采用的是将非线性函数在初值附近做Taylor展开，然后略去二次及二次以上诸项，做简单线性近似的方法，所以无法避免两种情况的发生：一是Gauss-Newton法对初值的依赖非常严重，如果初值选取不当，往往发散，即越迭代越远离目标值；二是如果Taylor展开后略去的二次及二次以上诸项的值相对过大，依然会造成Gauss-Newton法不收敛。

克服这个困难的一种途径是采用Levenberg-Marquardt的方法[9，10]，即加大 DF（X，Y，A0）TDF（X，Y，A0）的主对角元素，而得到改善，将步骤（3）中的方程改写成：

式中：μ——阻尼因子；

In——n阶单位矩阵或DF（X，Y，A0）TDF（X，Y，A0）的主对角元素构成的矩阵（本论文中的算法选择后者）。相应的算法步骤归纳如下：

（1）取初始近似值A0，计算

（2）取一个适中的μ值，如μ=0.001；

（3）计算 F（X，Y，A0），DF（X，Y，A0），DF（X，Y，A0）T；

（4）解线性方程组[DF（X，Y，A0）TDF（X，Y，A0）+μ In]△A=-DF（X，Y，A0）TF（X，Y，A0），得△ A，并计算 V（X，Y，a1，+V a1a2+V a2，L，an+V an，）；

（5）如果 V （X，Y，a1+V a1，α2+V a2，L，an+V an）≥ V（X，Y，a1，a2，L，an），则将 μ扩大 10 倍（或其他的具有意义的倍数），再回到步骤（4）；

（6）如果V（X，Y，a1+V a1，a2+V a2，L，an+V an）＜V（X，Y，a1，a2，L，an），则将μ缩小10倍（或者其他的具有意义的倍数），将△A+A0代替 A0，再回到步骤（4）；

（7）直至|△ A|＜ε或 V（X，Y，a1，a2，L,an）的变化量＜ε，迭代停止，输出结果。

[1]刘昌孝，刘定远.药物动力学概论[M].北京：中国学术出版社，1984.

[2]梁文权.生物药剂学与药物动力学[M].北京：人民卫生出版社，2000.

[3]袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2003.

[4]关治，陆金甫.数值分析基础[M].北京：高等教育出版社，2002.

[5]韦鹤平.最优化技术应用[M].上海：同济大学出版社，1987.

[6]谭浩强.C程序设计[M].2版.北京：清华大学出版社，2002.

[7]蒋长锦.科学计算和C程序集[M].合肥：中国科学技术大学出版社，1998.

[8]William H P，Saul A T，William T V，et al.C数值算法[M].2 版.北京：电子工业出版社，2004.

[9]张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004.

[10]肖爱玲.Some algorithms of nonlinear least squares[J].数学理论与应用，2004，24（2），86～90.

G431

A

1671-1246（2012）17-0042-03