基于混合边界条件的有限单元法GPR正演模拟

冯德山，陈承申，王洪华

1 中南大学 地球科学与信息物理学院，长沙 410083

2 有色金属成矿预测教育部重点实验室，长沙 410083

3 有色资源与地质灾害探查湖南省重点实验室，长沙 410083

1 引 言

探地雷达（Ground penetrating radar，GPR）正演模拟一直是该领域理论研究的热点[1-2］，通过对典型地质模型正演结果的分析，可以加深对GPR反射剖面的理解与认识[3-4］，对GPR资料解释具有指导作用.在GPR正演模拟中，时域有限差分法[5-7］（FDTD）因简单灵活而被广泛采用，但它不适合复杂的物性分界面.有限单元法（Finite Element Method，FEM）不需要计算内部边界条件，适用于物性复杂问题、求解过程规范化，具有广泛的适应性.

在地震波FEM模拟[8］得到快速发展的同时，一些学者将其引入到GPR正演模拟中：沈飚[9］进行了GPR简单模型正演；底青云和王妙月[10-11］推导了含衰减项的探地雷达波有限元方程，实现了复杂形体的GPR波的FEM正演模拟和偏移处理；Fanning和Boothby[12］将GPR有限元建模技术应用到拱桥检测中；谢辉等[13］基于二十节点等参单元的FEM对Pulse型GPR进行了模拟；Arias等[14］将有限元技术应用到GPR考古成像中；Lu等[15］利用离散时域Galerkin进行色散介质中的GPR正演.

GPR正演模拟是用有限空间模拟半无限大空间，在模型边界上必然产生边界反射.因此，需要在截断边界处使用一种特殊计算方法，在保证边界处场的计算精度的同时大大消除人工截断边界的反射波.如Cerjan边界条件[16］，它是在边界区引入一个衰减层，让波的能量在这个衰减层里呈现指数衰减，但是这种吸收边界条件的选取比较困难，衰减层的厚度、衰减系数的大小都要凭经验去估计.Sarma[17］在边界区域建立一个一定厚度的衰减层，根据材料性质估算恒定比例系数，使衰减层和介质区存在明显的物性差异，从而产生反射波；王月英等[18］提出了一种改进的Sarma边界条件，通过在衰减层内增加一定厚度的过渡带，过渡带内的比例系数呈现线性变化，这就使介质区和衰减层之间的物性差异渐变，大大减弱了交界面处的反射，但也存在对阻尼比的选取不敏感、过渡带和吸收层的交界面的角点处产生较强的绕射波的缺点，仍需寻求新的解决办法来取得更好的吸收效果.

本文通过对透射边界条件和改进Sarma边界条件的研究，提出一种混合边界条件.通过在研究区域外加载一定厚度的吸收层，以改进的Sarma边界条件对到达边界处的GPR波能量进行吸收衰减，然后在最外边加载透射边界条件，将衰减过的探地雷达波透射出去，这种混合边界条件集成了二者的优势，对人工截断边界的反射波取得更好的吸收效果.

2 GPR波动方程推导

Maxwell方程组描述了电磁场的运动学和动力学规律[19］，由电磁波理论，高频电磁波在媒质中的传播规律也应服从Maxwell方程组，其方程组的微分形式可以表示为[20-21］

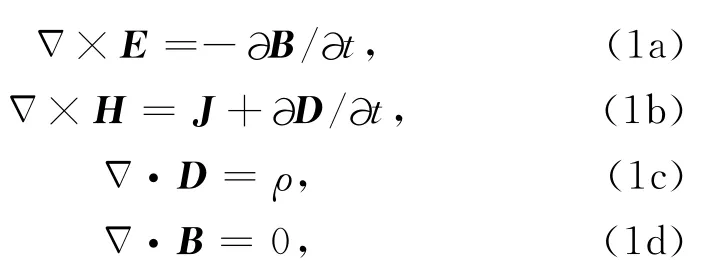
式中，E为电场强度（V／m），H为磁场强度（A／m），B为磁感应强度（T），D为电位移（C／m2），J为电流密度（A／m2），ρ为电荷密度（C／m3）.

本构方程：

式中ε为介电常数（F／m），μ为磁导率（H／m），σ为电导率（S／m）.

把方程式（2）代入方程式（1a），并求旋度，得

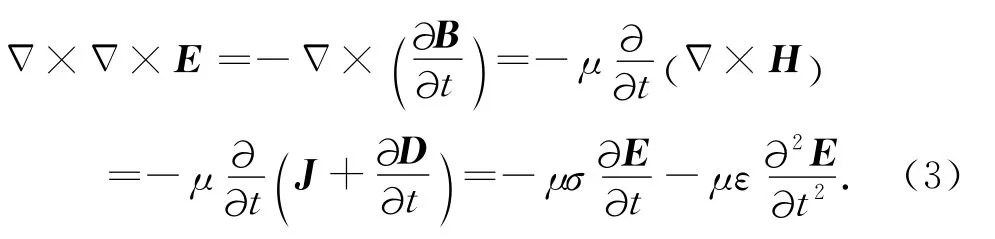
考虑到式

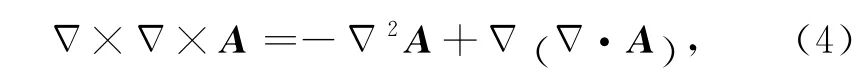
由于ε，μ，σ为坐标的函数，它们的时间导数可以忽略，用电场E取代（4）式中的A，则（4）式中右边第二项为0，整理得

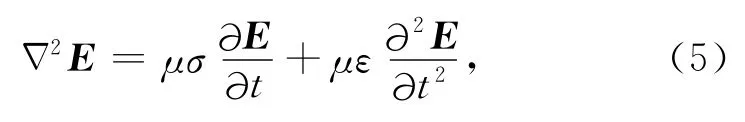
假设将雷达波激励源如电场源SE或磁场源SH，代入到（5）式中，有

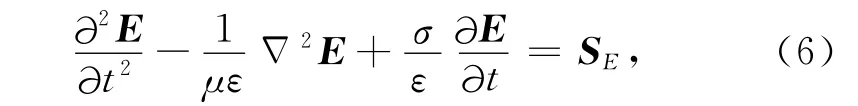
同理对（1b）式中第二式两边求旋度，可得下式：

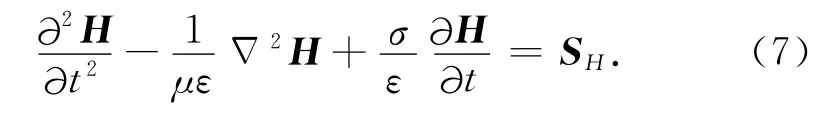
（6）、（7）两式表明，磁场H和电场E及其分量满足相同的微分方程.

3 GPR波动方程有限元求解

求解GPR波动方程其实质是结合雷达波所要满足的初、边值条件求解偏微分方程.边界条件分为两种类型[22］：Dirichlet边界条件与Neumann边界条件.变分法推导结果自动满足Dirichlet边界条件，即未知函数在边界上有已知值；伽辽金（Galerkin）法推导结果自动满足Neumann边界条件，即未知函数的导数在边界上有已知值.下面采用伽辽金法推导含衰减项的GPR有限元方程.

第1步 网格剖分

将求解的二维区域剖分成矩形单元，如图1所示.

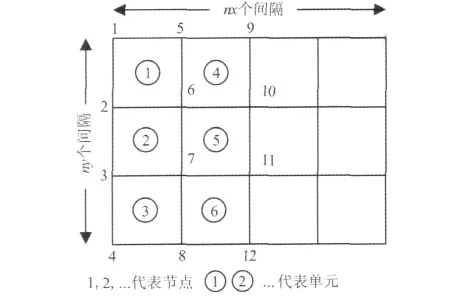
图1 网格剖分及节点编号示意图Fig.1 Sketch map of mesh division and node number

第2步 线性插值

设（x，y）是子单元的坐标，（x0，y0）是子单元中点的坐标，a、b是子单元的两个边长，（ξ，η）为母单元的坐标，两个单元间的坐标变换关系为

x=x0+（a／2）·ξ， y=y0+（b／2）·η， （8）其中微分关系为

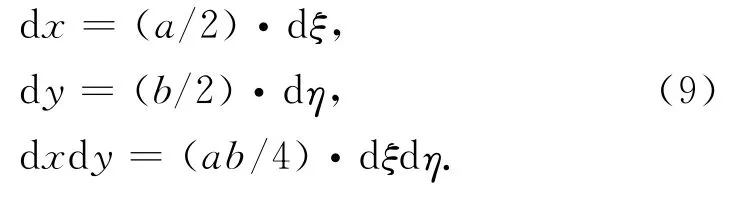
单元形函数为双线性插值形函数，可写为

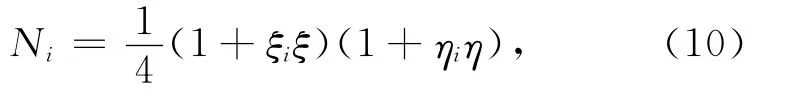
第3步 单元积分

根据伽辽金法，将（6）式两边同时乘以δE，并求积分，有

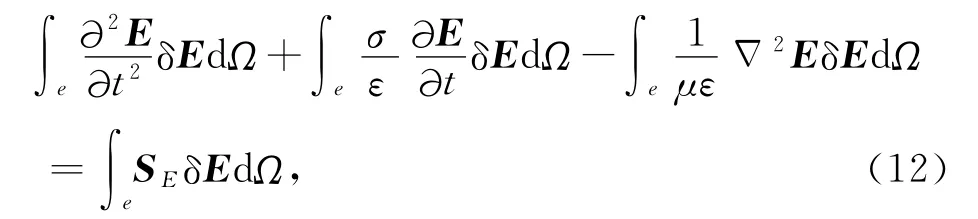
则式（12）左边第一项为

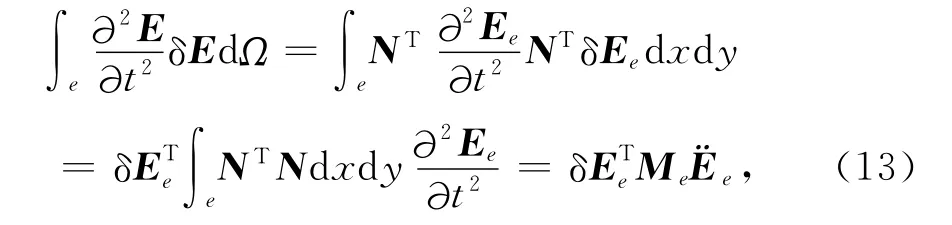
其中Me为单元质量矩阵：

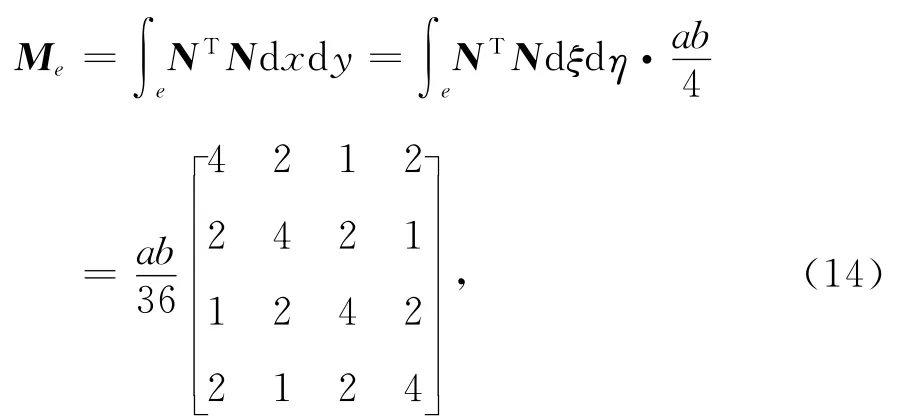
式（12）左边第二项为

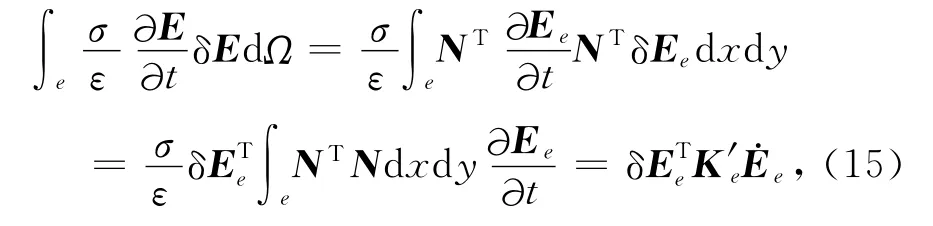
其中K′e为单元阻尼矩阵：

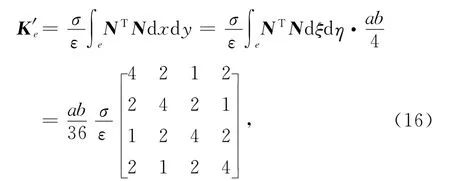
式（12）左边第三项为

其中Ke= （kij）= （kji）.

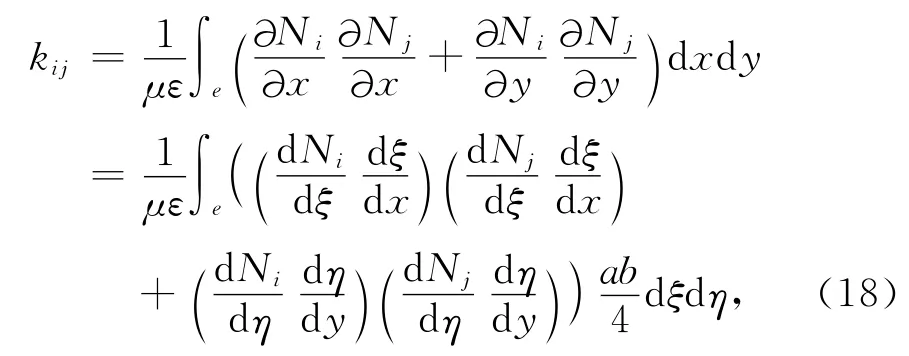
将（11）式求得ξ或者η的微商，代入到（18）式积分即可得到单元刚度矩阵kij为

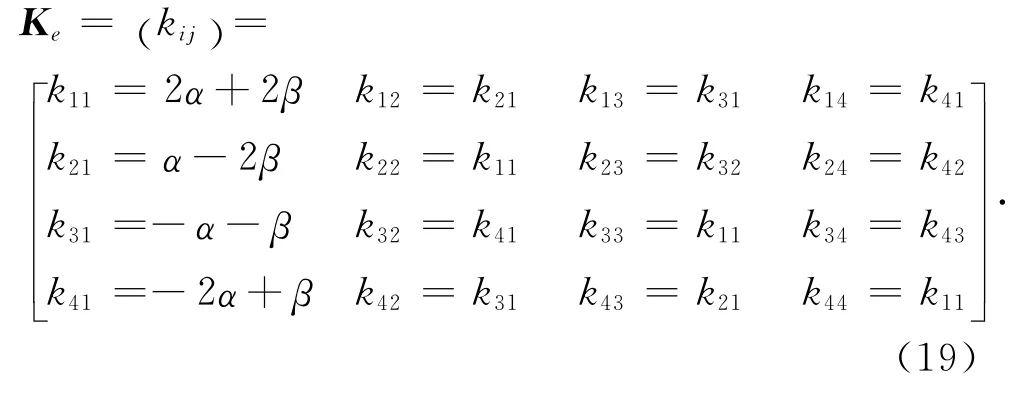
式（12）右边项为

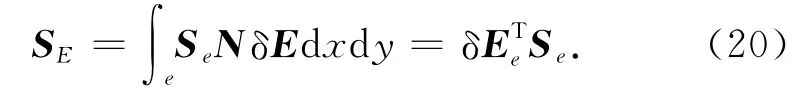
第4步 总体合成

根据式（13）、（15）、（17）、（20）得到单元积分：

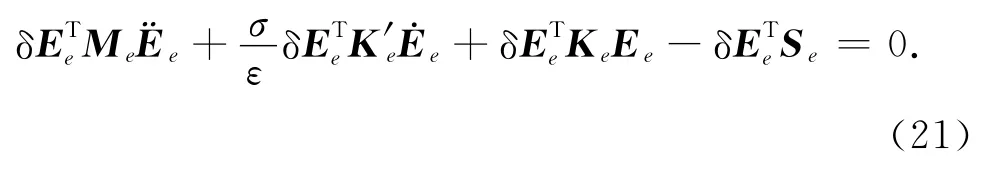
其中ND是节点总数.将4×4的系数矩阵Me、K′e和Ke扩展成ND×ND的矩阵M，K′和K，将列向量Se扩展成ND维列向量S，即

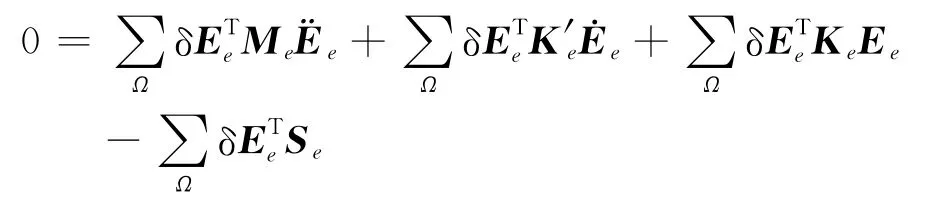
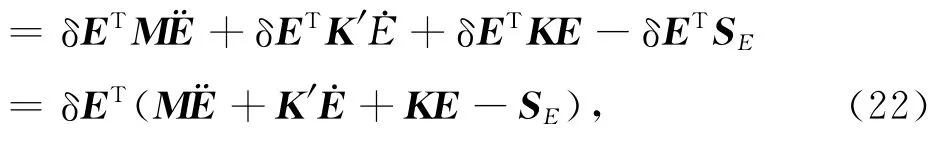
其中，

由于δET≠0，所以必有M¨E+K′E·+KE=SE.于是可以得到时空域GPR波的二维有限元方程，这是含有ND个元的ND个方程联合的常微分方程组，可以写成如下形式：

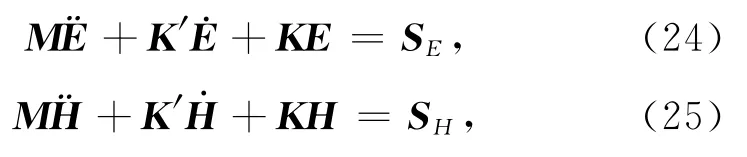
第5步 解GPR有限元常微分方程

解常微分方程组（24）或（25）前，要代入边界条件，边界条件的加载方法将在下节讨论.先采用中心差分法解方程（24）.对初始条件离散化得到E（0）=把时间域 [0，T］分为几个相等步长Δt=T／n，把时刻t的微分方程记为

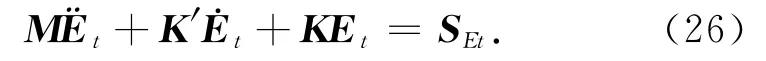
用差商代替微分：

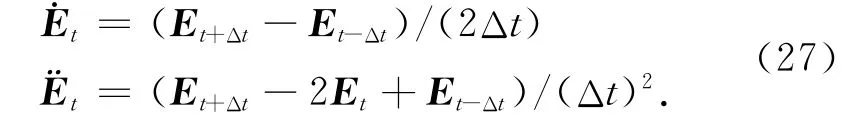
中心差分法是一种条件稳定的计算方法，当时间步长Δt取的过大时，计算结果就会出现数值色散，为此本文采用 Δt≤ （ΔXmin／Vmax），式中时间步长 Δt与最小单元边长ΔXmin成正比，与最大媒质速度Vmax成反比.差分网格空间步长满足稳定性条件Δx＜ （λmin／10），其中λmin为最小波长长度，Δx为单元的最小尺寸.将式（27）代入到式（26）中得到

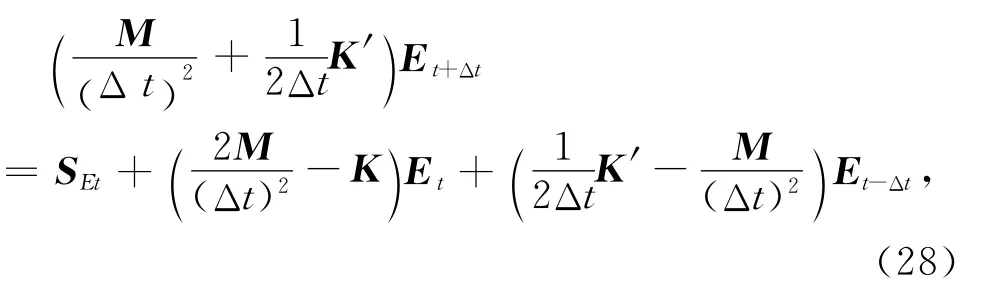
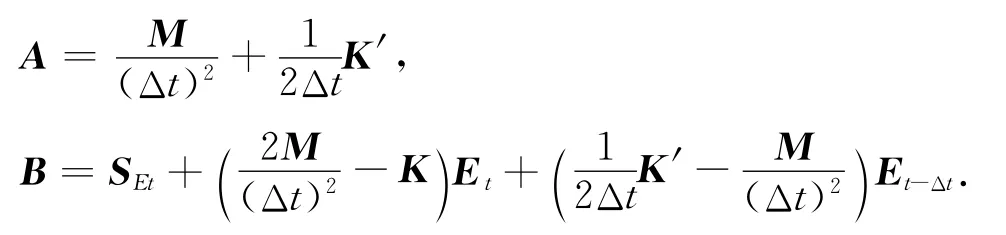
求解不含衰减项的GPR波动方程时，由于系数矩阵A往往是大型的病态稀疏矩阵，其条件数很大，如果采取对其直接求逆，计算量巨大，其求解结果不可信，只有当系数矩阵A是对角阵时，其逆矩阵是对角元素求倒数，这种方法才适用，为此采取集中质量矩阵方法来处理M矩阵，即将每一行（或列）的元素都加到对角线元素上去，则式（14）可转化为单元集中质量矩阵：

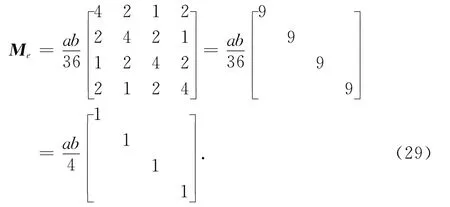
由于总体集中质量矩阵也有对角阵，所以不含衰减项的GPR有限元方程的差分迭代公式可写为

在求解含有衰减项的波动方程（28）时，系数矩阵A是质量矩阵M 和阻尼矩阵K′的线性组合，同样可以采用单元集中质量矩阵求解.但本文中选用不完全LU分解预处理的BICGSTAB（Biconjugate Gradient Stabilized）线性方程组求解算法[23-24］，该算法是一种高效迭代法，特别适用于求解条件数很大的病态线性方程组.

4 混合边界条件理论

目前应用于电磁场正演模拟的边界条件主要集中于FDTD相关算法，如辐射边界条件[25-26］、基于单行波方程的吸收边界条件[27-28］、超吸收边界条件[29］、完全匹配层（PML）[30-31］吸收边界条件等.而GPR有限元法正演模拟文献较少，采用的吸收边界条件多借鉴与地震波有限元正演模拟的吸收边界条件.下面主要介绍透射边界条件与Sarma吸收边界条件，在此基础上提出了混合边界条件.

4.1 透射边界条件

透射边界条件是通过直接模拟各种单向波动的共同运动学特征来建立的一种边界条件，原理简单易懂，算法容易实现.首先给出穿过人工边界上一点并沿边界外法线方向传播的单向波动的一般表达式，并假定所有单向波动以同一人工波速沿法线方向从边界透射出去，由此可得透射边界条件公式[32］：

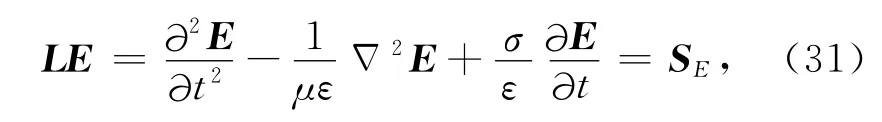
式中L为微分算子.在每个单元中有

这里Ei为每个单元上第i个节点的电场值.残余量R为

利用伽辽金余量法，二维有限元方程可写为

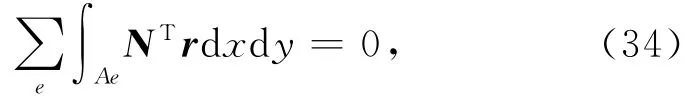
其中Ae为单元面积，r是残余量R的向量表示，由式（32）代入式（33）得到.

由于内边界的积分相互抵消，所以只需求解图2所示的区域外边界积分.在均匀各向同性介质中，

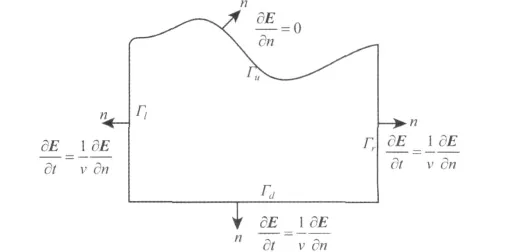
图2 区域外边界条件Fig.2 Boundary condition outside the area

根据Claerbout[33］推导的旁轴近似，其下行波方程为

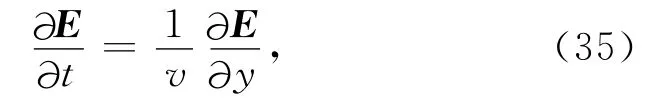
左行波方程为

右行波方程为

由法向导数的定义知

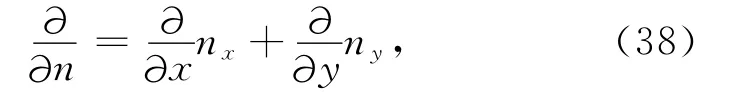
其中，nx和ny为边界外法线的方向余弦.

将式（31）、（32）、（33）代入式（34）中，并利用高斯定理可得

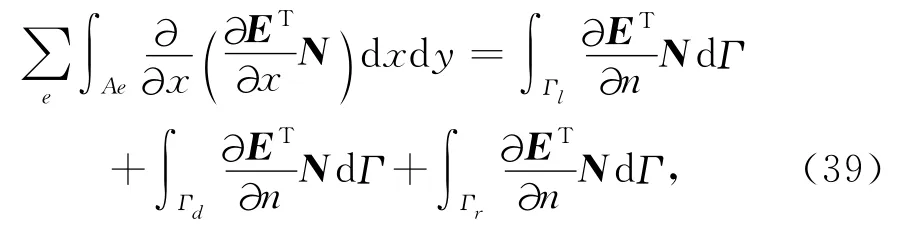
其中Γl、Γr、Γd分别表示左、右及底边界，上边界为自由边界条件.

将式（35）、（36）、（37）给出的边界条件代入到式（39），可以得到：

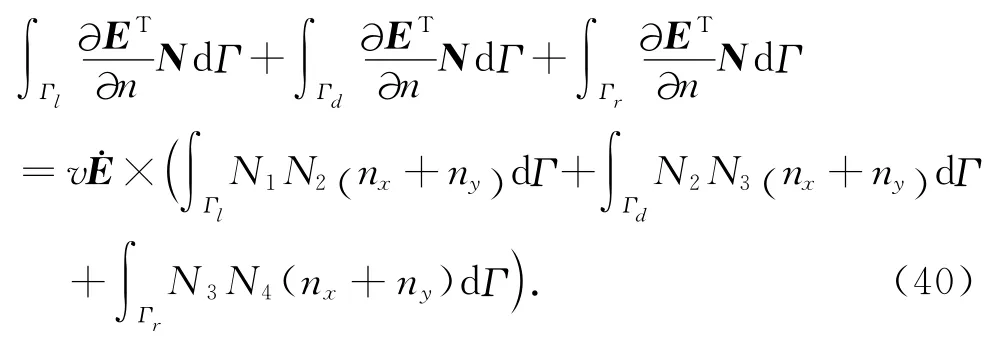
在加载透射边界条件时，还需求解外法线的方向余弦，其求解示意如图3所示.θx为GPR发射天线激励源和边界线单元x方向的夹角，θy为y方向夹角，无论这两个角是正还是负，其余弦值nx和ny均为正值.

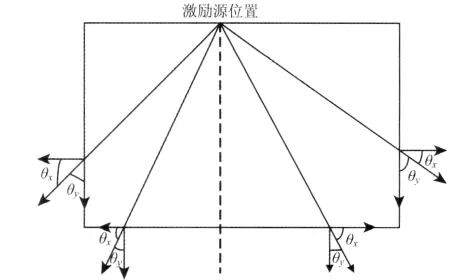
图3 外法线的方向余弦角示意图Fig.3 Sketch map of direction Cosine angle of external normal

在求解左边界的边界条件时，如图4所示，令N1= （1-ξ）／2，N2= （1+ξ）／2，dΓ=l·dξ／2，这里l为边界上的单元宽度，例如AB、CD边l=b，BC边l=a.先分析边界单元在AB边的情况：

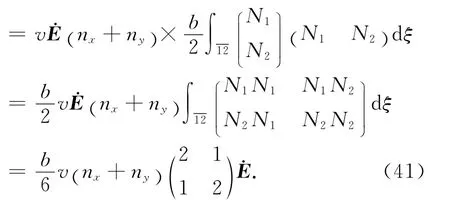
图4 边界上的单元Fig.4 Elements on the boundary

将边界的单元系数矩阵定义为Fe，则左边界的边界单元系数矩阵扩展为Fle：

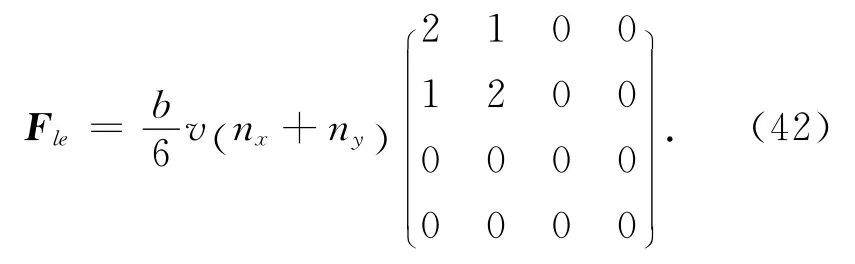
同理，可以求得底边界单元系数矩阵Fde和右边界单元系数矩阵Fre：

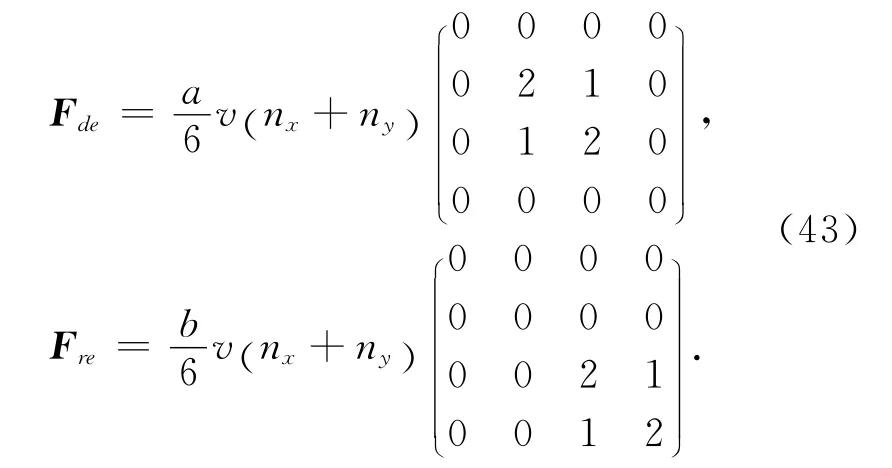
故边界的阻尼矩阵F为

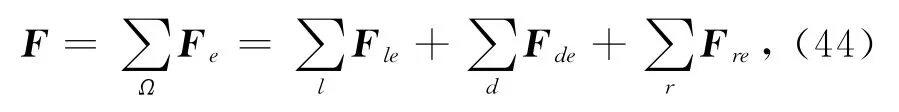
将边界阻尼加入到GPR有限元方程中去，得到如下式子：

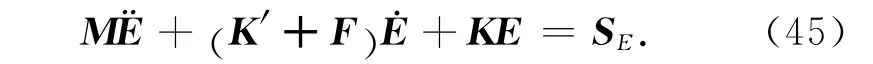
将（45）式透射边界条件结合式（24）就可以进行GPR有限元正演模拟.

4.2 Sarma吸收边界条件

Sarma吸收边界条件是在求解空间外的区域增加一个由衰减性媒质组成的衰减层，如图5a所示.对于衰减性媒质，阻尼力作用比较复杂，导致阻尼矩阵C不容易确定.Rayleigh在1877年给出了一种计算阻尼矩阵C的经典方法，该方法[34］是利用整体质量矩阵M和整体刚度矩阵K来计算阻尼矩阵C：

图5 Sarma边界条件及其改进模型示意图（a）Sarma边界条件；（b）改进的Sarma边界条件；（c）优化过渡带角点的Sarma边界条件.Fig.5 Sketch map of Sarma boundary condition and improved model（a）Sarma boundary condition；（b）Improved Sarma boundary condition；（c）Sarma boundary condition of optimized transitional layer.

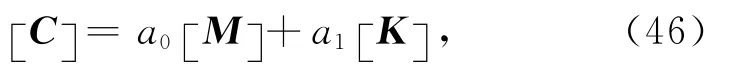
其中，

式中ωi和ωj分别为介质的第i和第j个固有的圆频率，ξi和ξj为对应的阻尼比.

Caughey[35］提出了一种更为普遍的阻尼矩阵计算公式：

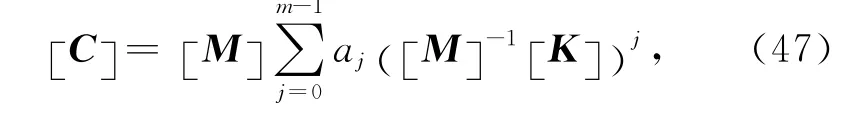
可以看出（46）式是（47）式的二阶形式，即m=2，体现了质量矩阵和刚度矩阵的线性组合，并且这种组合非常容易计算，其单元中的计算公式如下：

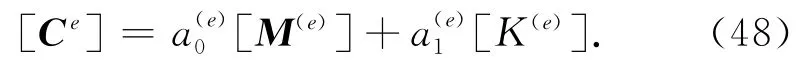
对于二阶Caughey阻尼矩阵的两个系数a0和a1与阻尼比ξ存在着如下的关系：

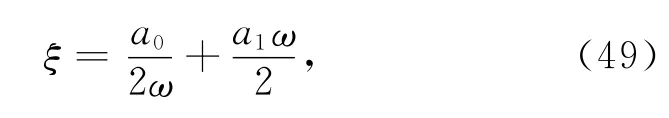
其中ω为发射天线的中心频率，通常0.05≤ξ≤0.30.将二阶Caughey阻尼矩阵引入到GPR吸收边界的处理中，得到吸收边界区内的有限元方程为

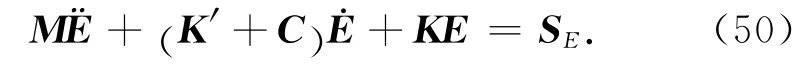
在衰减层内的比例系数a0和a1可由式（49）得到，这种方法虽然可行，但是衰减层和介质区还是存在着明显的物性差异，这种差异必然会在交界面处产生人为的反射波.针对Sarma边界条件在交界面处产生的人为反射波，王月英等[18］提出了一种改进方法，如图5b所示：即在衰减层内添加一个过渡带，过渡带内比例系数由零逐渐增大到a0和a1，衰减层取一个半波长的厚度，过渡带大约占半个波长.但该改进的Sarma边界条件在过渡带的四个角点位置仍存在着差异明显的四个小边界，为此本文采用一圈一圈的环形过渡带加载办法，消除了这种角点的人为差异，称之为优化过渡带角点的Sarma边界条件，如图5c所示.

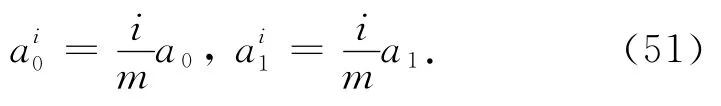
其中，衰减层内总节点数为n，过渡带内的节点数为m，m＜n（0≤i＜m）为过渡带内节点i处的比例系数，比例系数从交界面向衰减层边缘方向呈线性增长关系，这种方法就减缓了交界面处的物性参数突变，从而减小交界面处产生的人为反射波能量，比例系数增大到a0和a1就保持恒定，以确保GPR波在衰减层内能得到充分吸收.既能使交界面处的反射得到大大降低，又能让边界处的GPR波能量被充分吸收.

4.3 混合吸收边界条件

通过对透射边界条件和Sarma边界条件的深入分析，提出了一种结合两种边界条件的混合边界条件（如图6所示），其主要思想是利用Sarma边界条件对到达边界区域的电磁波能量衰减功能和透射边界对电磁波能量的透射功能，使GPR波经过Sarma边界条件的衰减吸收后再通过透射边界条件将剩余能量透射出去，集成了二者的优势.处理办法是在计算区域外面加一吸收层，用改进的Sarma边界条件使GPR波能量被吸收减弱，然后在最外边加载透射边界条件.通过改变公式（48）中给的阻尼比ξ，可以实现调节Sarma边界的吸收作用，从而和透射边界条件相互协作，达到最佳吸收效果.

5 不同边界条件的有限元模拟对比实例

图6 混合边界条件模型示意图Fig.6 Sketch map of mixed boundary condition

运用Matlab编制的有限元GPR模拟程序对10.0m×5.0m均匀模型进行了模拟，介质的介电常数ε=3.0，电导率σ=0.001S·m-1.网格单元大小为0.1m的正方形，GPR脉冲激励源的子波形式为f（t）=t2e-atsinω0t，其中ω0为发射天线中心频率为100MHz，电磁波脉冲的衰减速度取决于系数α，此处取α=0.93ω0.得到了半空间图7所示的不带边界条件的雷达正演wiggle图.图中可见，A、B为左右边界的反射波，C为底边界的反射波，D、E为左下角和右下角的两个角点的绕射波.这些人为截断边界的反射强度很大，对观测区域影响严重，说明了对截断边界的处理势在必行.

5.1 透射边界条件中心脉冲激励源模型仿真

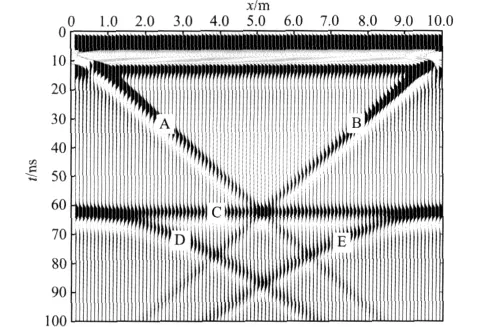
图7 不带边界条件的均匀模型wiggle图Fig.7 Wiggle diagram for homogeneous model without boundary conditions

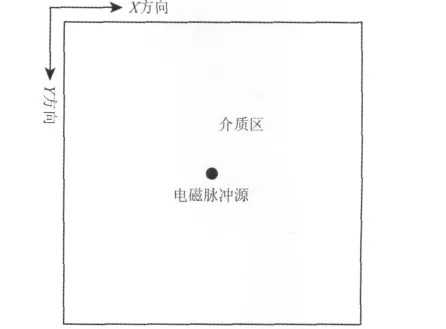
图8 均匀模型示意图Fig.8 Sketch map of homogeneous model

为了更好地说明不同吸收边界条件对人工截断边界反射波的吸收效果，建立图8所示9.0m×9.0m大小的正方形均匀模型，并把脉冲激励源置于模拟区域的正中心，采样时间间隔为0.5ns，其它参数与无边界条件情况下一致.通过截取不同时刻的波场快照图，观测不同边界条件对人工截断边界的吸收效果.图9（a，b，c）分别为不带边界条件的20、30ns、35ns波场快照，图中可见在30ns时刻GPR波前开始传到区域边缘，人为截断边界反射波开始形成，从35ns快照图可以看出，人为截断边界反射回的GPR波能量很强，严重影响到对目标区域的研究，同样说明，截断边界的处理是非常必要的.

图10（a，b，c）分别为模型边界处加载透射边界的30、35、40ns波场快照.图中可见，在30ns时，波的能量刚刚传播到边界区域，在35ns时可以看出电磁波大部分的能量都从边界处透射出去，只有少部分的能量反射回来，对比图9c相同时刻的截断边界处的强反射波能量，说明了透射边界条件取得了显著效果.但是再分析图10c中40ns的波场快照图仍然可以看到截断边界的反射回波，说明透射边界条件仍有待改进.

5.2 改进的Sarma边界条件中心脉冲激励源模型仿真

仍以上例模型和相应参数为例，分别以Sarma边界条件、改进的Sarma边界条件和优化了过渡带的Sarma边界条件对截断边界进行了处理.图11a为没有加载过渡带的Sarma边界条件的30ns波场快照图，由于没有加载过渡带，在介质区和衰减层之间的界面产生了明显的反射和角点绕射；图11b为改进Sarma边界条件的30ns波场快照图，由于加载了过渡带，在介质区和边界吸收层之间的媒质特性是渐变的，明显的减弱了介质之间的差异，降低了介质区和边界吸收层之间界面的反射波能量，较好地处理了介质区和衰减层之间物性差异引起的反射波，但在过渡带的四个角点位置存在着差异明显的四个小边界.为了消除这种因过渡带人为加载方式引起的反射，本文采用一圈一圈的环形过渡带加载办法，图11c为优化过渡带Sarma边界条件的30ns波场快照图.它是在改进的Sarma边界条件基础上，对过渡带的加载方法进行了优化，目的是减少人为的角点引起的异常，虽然效果不是很明显，但是从侧面反映出改进的Sarma边界条件的过渡带的角点异常主要是由角点引起，过渡带的加载方法并非主要影响因素，重点工作应该放在研究过渡带的角点异常消除上.

5.3 混合吸收边界条件中心中心脉冲激励源模型仿真

如图12a为加载了透射边界条件的35ns快照图，图12b为加载了优化过渡带的Sarma边界条件的35ns快照图，图12c为加载混合边界条件的35ns快照图.图中可见，图12b优化过渡带的Sarma边界条件由于过渡带的四个角点区的绕射波能量比较强，其对GPR波的吸收效果并不是很理想，而图12c中的混合边界条件由于集成了Sarma边界条件和透射边界条件的优点，先衰减了到达边界区域的GPR波能量，然后再将其透射出去，观察相同时刻快照图，可以看出，与图9c无边界条件的波场快照图对比，各种边界条件对截断边界处的反射波都取得了良好效果，但混合边界条件明显优于单纯的透射边界条件或Sarma边界条件.

6 探地雷达正演模拟实例

6.1 起伏界面模型

如图13所示，模型为一个10.0m×5.0m的矩形区域，分为上下两层介质，中间是起伏界面，上层介质的相对介电常数ε1为3.0，电导率σ1为0.001S·m-1，下层介质的相对介电常数ε2为20.0，电导率σ2为0.01S·m-1，整个区域由单元边长0.1m的正方形，网格剖分为100×50的网格空间，GPR波脉冲激励源的中心频率为100MHz，采样时窗长度为100ns，采样时间间隔为0.5ns.应用本文的基于混合边界条件的FEM算法对起伏界面模型进行了正演模拟，得到了图14所示的GPR正演模拟wiggle图，图中可见，在30ns附近有一条能量较强的反射界面，通过计算可以得出它与图13模型中的上、下两层分界面位置相吻合，但是在起伏比较大的地方，仍存在角点绕射现象.

6.2 三角形与阶梯模型

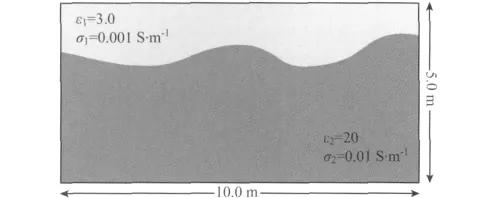
图13 起伏界面模型示意图Fig.13 Sketch map of undulating interface

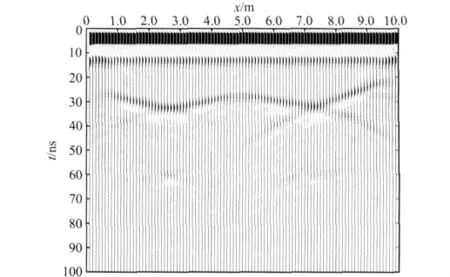
图14 起伏界面模型探地雷达正演模拟wiggle剖面图Fig.14 Wiggle section for forward simulation of GPR

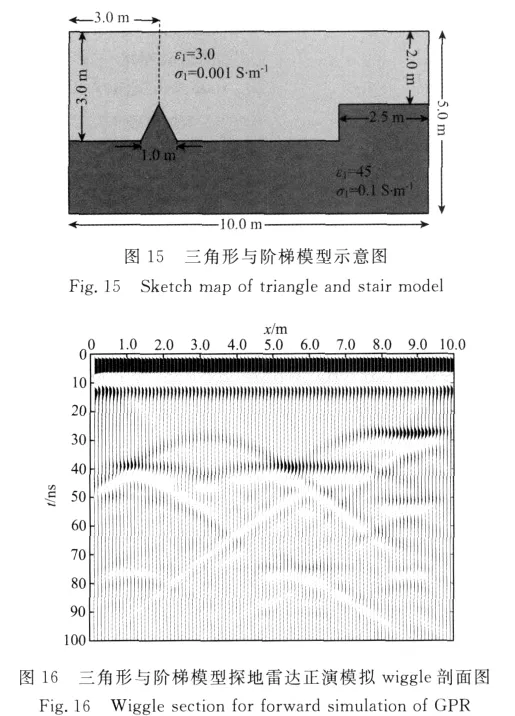
如图15所示，模型为一个10.0m×5.0m的矩形区域，分为上下两层介质，中间是特殊形态的起伏界面，包括一个三角形和一个阶梯，上层介质的相对介电常数ε1为3.0，电导率σ1为0.001S·m-1，下层介质的相对介电常数ε2为45.0，电导率σ2为0.1S·m-1，整个区域由单元边长0.1m的正方形网格剖分为100×50的网格空间，GPR波源、时窗长度、采样时间间隔均与上面模型一致.应用FEM算法对起伏界面模型进行了正演模拟，得到了图16所示的三角形与阶梯模型的GPR正演模拟wiggle图，分析该剖面图可以看出，在三角形顶点、阶梯形的断点处都存在较强的角点绕射波，而相应的平界面还会产生较强的反射波，模拟结果说明了FEM进行GPR正演模拟的正确性与可性性.

7 结论及建议

（1）推导了GPR有限元波动方程，给出了有限单元法求解该泛函变分问题的详细解法，并结合差分离散时，时间步长与空间步长须满足的数值稳定性条件，探讨了GPR有限元波动方程是否带衰减项的不同求解算法.

（2）阐述了透射边界条件和Sarma边界条件的原理.着重对Sarma边界条件进行了研究，并通过在Sarma边界条件衰减层内以环状方式加入过渡层，压制了介质区和衰减层交界面处的人为反射，优化了Sarma边界条件.并以二维均匀模型的中心脉冲激励源为例，对比了人工截断边界处不同边界条件的处理效果.

（3）提出了一种结合透射边界条件和Sarma边界条件的混合边界条件，使GPR波经过Sarma边界条件的衰减吸收后再通过透射边界条件将剩余能量透射出去，集成了两种边界条件的优势.最后应用基于该混合边界条件的FEM算法对两个典型地电模型进行了正演模拟，模拟结果表明，混合边界条件有效地消除了截断边界处的强反射，说明了FEM算法进行GPR正演模拟的有效性及可行性.

致 谢 中国科学院地质与地球物理研究所底青云教授对论文的有限元理论、中国石油大学（北京）资源与信息学院地质与地球物理综合研究中心的王月英老师对Sarma边界条件程序编制方面给予了有益帮助，在此一并致以衷心的谢意.

（References）

[1]Feng D S，Dai Q W.GPR numerical simulation of full wave field based on UPML boundary condition of ADI-FDTD.NDT &E International，2011，44（6）：495-504.

[2]Shaari A，Ahmad R S，Chew T H.Effects of antenna-target polarization and target-medium dielectric contrast on GPR signal from non-metal pipes using FDTD simulation.NDT &E International，2010，43（5）：403-408.

[3]James I，Rosemary K.Numerical modeling of groundpenetrating radar in 2-D using MATLAB.Computers &Geosciences，2006，32（9）：1247-1258.

[4]Giannopoulos A.Modelling ground penetrating radar by GprMax.Construction and Building Materials，2005，19（10）：755-762.

[5]刘四新，曾昭发，徐波.三维频散介质中地质雷达信号的FDTD数值模拟.吉林大学学报 （地球科学版），2006，36（1）：123-127.Liu S X，Zeng Z F，Xu B.FDTD simulation for ground penetrating radar signal in 3-Dimensional dispersive medium.Journal of Jilin University （Earth Science Edition）（in Chinese），2006，36（1）：123-127.

[6]Bergmann T，Robertsson J O A，Holliger K.Numerical properties of staggered finite-difference solutions of Maxwell＇s equations for ground-penetrating radar modeling.Geophysical Research Letters，1996，23（1）：45-48.

[7]Carcione J M.Radiation patterns for 2-D GPR forward modeling.Geophysics，1998，63（2）：424-430.

[8]王妙月，郭亚曦，底青云.二维线性流变体波的有限元模拟.地球物理学报，1995，36（4）：499-506.Wang M Y，Guo Y X，Di Q Y.2-D finite element modelling for seismic wave in media with linear rheological property.Acta Geophysica Sinica （in Chinese），1995，36（4）：499-506.

[9]沈飚.探地雷达波波动方程研究及其正演模拟.物探化探计算技术，1994，16（1）：29-33.Shen B.A study on wave equation theory for groundpenetrating radar and forward modelling.Computing Techniques for Geophysical and Geochemical Exploration（in Chinese），1994，16（1）：29-33.

[10]底青云，王妙月.雷达波有限元仿真模拟.地球物理学报，1999，42（6）：818-825.Di Q Y，Wang M Y.2Dfinite element modeling for radar wave.Chinese J.Geophys.（in Chinese），1999，42（6）：818-825.

[11]Di Q Y，Wang M Y.Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion.Geophysics，2004，69（2）：472-477.

[12]Fanning P J，Boothby T E.Three-dimensional modelling and full-scale testing of stone arch bridges.Computer &Structures，2001，79（29）：2645-2662.

[13]谢辉，钟燕辉，蔡迎春.电磁场有限元法在GPR正演模拟中的应用.河南科学，2003，21（3）：295-298.Xie H，Zhong Y H，Cai Y C.Application of finite element methods for electromagnetic fields in forward model of GPR.Henan Science（in Chinese），2003，21（3）：295-298.

[14]Arias P， Armesto J， Capua D D， et al.Digital photogrammetry，GPR and computational analysis of structural damages in a mediaeval bridge.Engineering Failure Analysis，2007，14（8）：1444-1457.

[15]Lu T，Cai W，Zhang P W.Discontinuous galerkin timedomain method for GPR simulation in dispersive media.IEEE Transactions on Geoscience and Remote Sensing，2005，43（1）：72-80

[16]Cerjan C，Kosloff D，Kosloff R.A nonreflecting boundary condition for discrete acoustic and elastic wave equations.Geophysics，1985，50（4）：705-708.

[17]Sarma G S，Mallick K，Gadhinglajkar V R.Nonreflecting boundary condition in finite-element formulation for an elastic wave equation.Geophysics，1998，63（3）：1006-1016.

[18]王月英，宋建国.波场正演模拟中Sarma边界条件的改进.石油物探，2007，46（4）：359-362，389.Wang Y Y，Song J G.Improvement of Sarma boundary condition in wavefield forward modeling.Geophysical Prospecting for Petroleum （in Chinese），2007，46（4）：359-362，389.

[19]Yee K S.Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media.IEEE Transactions on Antennas and Propagation，1996，14（3）：302-307.

[20]Taflove A.Re-inventing electromagnetics：supercomputing solution of Maxwell＇s equations via direct time integration on space grids.Computing Systems in Engineering，1992，3（1）：153-168.

[21]Alvarez G B，Loula A F D，Dutra do Carmo E G，et al.A discontinuous finite element formulation for the Helmholtz equation.Computer Methods in Applied Mechanics and Engineering，2006，195（33-36）：4018-4035.

[22]徐世浙.地球物理中的有限单元法.北京：科学出版社，1994：260-277.Xu S Z.The Finite Element Method in Geophysics（in Chinese）.Beijing：Science Press，1994：260-277.

[23]Van der Vorst H A.Bi-CGSTAB：A fast and smoothly converging variant of BI-CG for the solution of nonsymmetric linear systems.SIAM Journal on Scientific and Statistical Computing，1992，13（2）：631-644.

[24]柳建新，蒋鹏飞，童孝忠等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用.中南大学学报 （自然科学版），2009，40（2）：484-491.Liu J X，Jiang P F，Tong X Z，et al.Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling.Journal of Central South University（Science and Technology）（in Chinese），2009，40（2）：484-491.

[25]Kriegsmann G， Morawetz C S.Numerical solutions of exterior problems with the reduced wave equation.Journal of Computational Physics，1978，28（2）：181-197.

[26]Bayliss A，Turkel E.Boundary conditions for the helmholtz equation in duct-like geometries.International Association for Mathematics &Computers in Simulation，1983，455-458.

[27]Engquist B，Majda A.Absorbing boundary conditions for numerical simulation of waves.ProceedingsoftheNational AcademyofSciencesoftheUnitedStatesofAmerica，1977，74（5）：1765-1766.

[28]Mur G.Absorbing boundary conditions for the finitedifference approximation of the time-domain electromagneticfield equations.IEEE Transactions on Electromagnetic Compatibility，1981，23（4）：377-382.

[29]Mei K K，Fang J Y.Superabsorption-a method to improve absorbing boundary conditions.IEEE Transactions on Antennas and Propagation，1992，40（9）：1001-1010.

[30]Gedney S D，Liu G，Roden J A，et al.Perfectly matched layer media with CFS for an unconditionally stable ADI-FDTD method.Antennas and Propagation IEEE Transactions on，2001，49（11）：1554-1559.

[31]Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves.Journal of Computational Physics，1994，114（2）：185-200.

[32]薛东川，王尚旭，焦淑静.起伏地表复杂介质波动方程有限元数值模拟方法.地球物理学进展，2007，22（2）：522-529.Xue D C，Wang S X，Jiao S J.Wave equation finite-element modeling including rugged topography and complicated medium.Progress in Geophysics（in Chinese），2007，22（2）：522-529.

[33]Claerbout J F.Imaging the Earth′s Interior.Boston：Blackwell Scientific Publications，1985.

[34]Semblat J F，Gandomzadeh A L L.A simple numerical absorbing layer method in elastodynamics.Comptes Rendus Mécanique，2010，338（1）：24-32.

[35]Caughey T K.Classical normal modes in damped linear dynamic systems.Journal of Applied Mechanics，1960，27（2）：269-271.