编码器正余弦信号跟踪环路细分技术研究

，，，

（华中科技大学 机械科学与工程学院，湖北 武汉 430074）

1 引言

在高精度运动控制中通常采用输出正余弦信号的位置检测元件进行位置和速度反馈。这样的位置检测元件包括旋转编码器、直线光栅尺、圆光栅、旋转变压器或者球栅尺等。对于生产商来说，设计基于正余弦信号的光学编码器远比设计带有大量行编号的TTL编码器容易［1］，用户通过合适的插值方法可以从正余弦信号中提取高分辨率的位置信息，并且这种模拟量的正余弦信号频率成分单一，与方波相比可以传输较远的距离而不衰减或者畸变［2］。如何从正余弦信号中提取出位置信息，尤其是提取出高分辨率的位置信息一直是国内外研究的主要课题。

从正余弦信号中提取位置信息通常称为正余弦信号的细分。正余弦细分一般包括硬件细分和软件细分2种方式。硬件细分中比较成熟的是电阻链细分技术，文献［2－3］对电阻链细分技术做了详细的论述。理论上电阻链细分可以达到很高的细分数，但是实际上随着细分数的提高，对电阻的阻值精度要求越来越高，并且后续电路中所用比较器数量也会成倍增加，不利于高倍细分。

高倍细分中通常都采用软件细分，正余弦信号携带的位置信息与正余弦信号的相位信息一一对应，细分的主要目的是从正余弦信号中提取相位信息。根据细分方式的不同，软件细分又包括开环细分和闭环细分2种方法。开环细分根据正弦值和余弦值直接提取相位信息，其原理如下式：

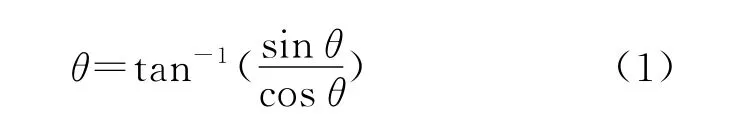
求取反正切有2种方法：文献［4－5］介绍了查表的方法；文献［6－8］介绍了通过CORDIC算法计算反正切值的方法。实验证明，通过这2种方法得到的结果都只包含了1个正余弦周期中的相位信息，不包括多个周期中的位置信息，因此除了对单圈正余弦信号细分外，这种细分一般采用粗精细分相结合的方法［5］。然而粗精细分的途径不一样，粗精细分的跳变沿通常是不同步的，这影响了细分结果线性度。另外，正余弦信号质量直接影响了反正切的相位值，为了达到较高倍数的细分必须对正余弦信号滤波。因为电机转速范围通常较大，故编码器正余弦信号的频率范围也较大，通常情况下噪声频率与信号频率部分重叠，故增加了滤波器的设计难度。文献［7－8］在信号处理中增加了FIR滤波器，这种滤波器对正余弦信号的滤波效果很有限，并且增加了系统硬件资源。

本文提出了一种环路跟踪细分的方法，该方法是根据闭环细分原理提出来的。这种方法容易用FPGA实现，对信号噪声抑制效果较开环细分方法好，可以达到1 024细分以上。

2 环路跟踪细分法原理

环路跟踪细分法是基于闭环细分的思路，其细分原理如图1所示。

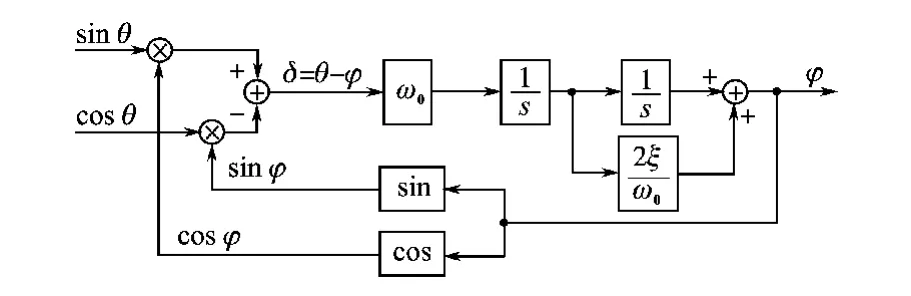
图1 环路跟踪框图Fig.1 The block diagram of tracking－loop

θ是当前时刻的位置值，φ是上一时刻的位置值。环路跟踪细分主要基于以下三角函数式：

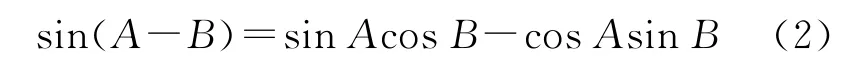
将A，B分别用θ，φ替换可以得到：

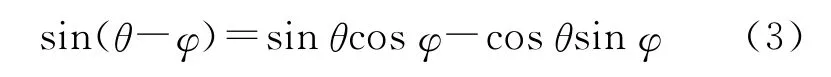
对于很小的位置变化量δ＝θ－φ有

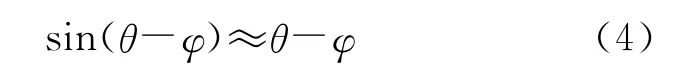
将式（3）代入式（4）得到

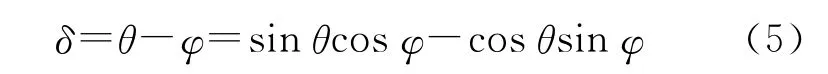
将位置变化量δ＝θ－φ代入PI控制器。负反馈的目的是将位置变化量减小到零。同时，通过PI控制器建立了1个二阶低通滤波器，该滤波器是对位置变化量滤波而非直接对正余弦信号滤波，极大地抑制了噪声。

将图1简化为图2，可以求得系统的传递函数为

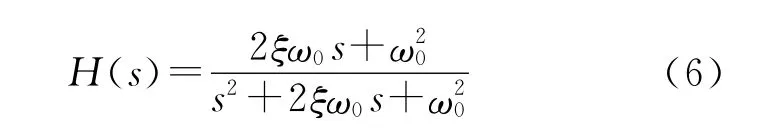
ω0和ξ决定了系统的固有频率和阻尼系数。对最大输入信号频率fmax＝1kHz，ω0＝2πf0＝628 000rad／s。ω0确定后不同ξ对系统响应和超调量的影响如图3所示。可以根据系统需求选择合适的固有频率和阻尼系数。

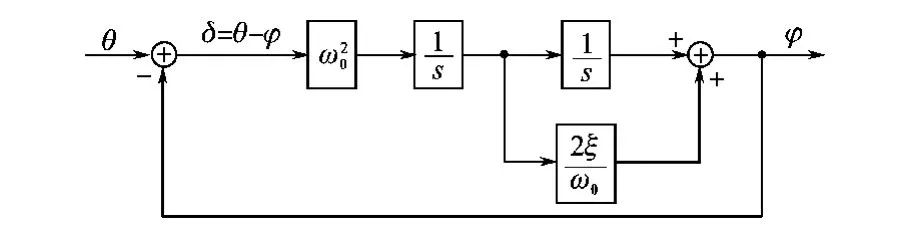
图2 简化的跟踪环路框图Fig.2 The simplified block diagram of the tracking－loop

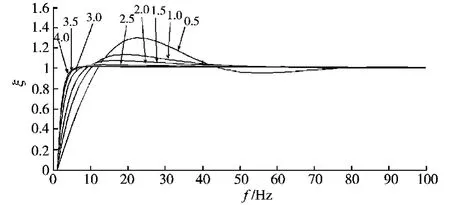
图3 系统动态响应Fig.3 The dynamic response of the system

3 环路跟踪细分的实现

3.1 系统硬件结构

环路跟踪细分与开环求反正切细分的硬件结构相同，都是通过由运算放大器构成的差分接收电路将输入的正余弦信号转换为单端信号，再通过AD采样，将正余弦信号送至FPGA做处理。FPGA细分后的数据频率远远高于输入信号频率，对传输接口和电缆以及电磁干扰性要求较高，所以细分后的信号通常通过串行传输协议打包输出。常见的协议形式有Endat，Biss，Hiperface等等。系统硬件结构图如图4所示。

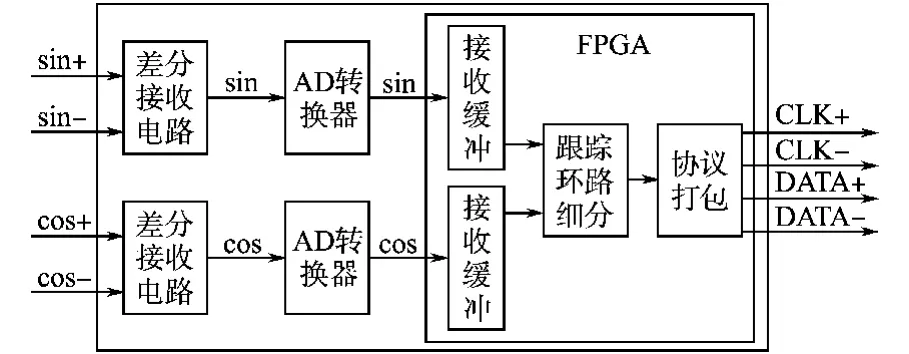
图4 系统硬件结构图Fig.4 The structure diagram of the system hardware

3.2 跟踪环路算法的FPGA实现

根据图1可知，跟踪环路细分算法中主要用到了乘法器、积分器和正余弦函数模块。其中乘法器可以直接采用硬件乘法器，积分器可以通过简单的VHDL实现，不再赘述。这里主要介绍正余弦函数的实现。

CORDIC算法将直角坐标中复杂的算术运算转换为极坐标中简单的加法移位操作，简化了三角函数的计算，因此文中通过CORDIC算法实现正余弦函数。限于篇幅CORDIC算法的原理这里不再做详细的介绍，可以参考文献［6，9］。CORDIC算法特别适合采用流水线结构设计。CORDIC算法的单次迭代结构图如图5所示，CORDIC算法模块主要由移位寄存器和加法器组成。对16位迭代需要15级迭代流水线。

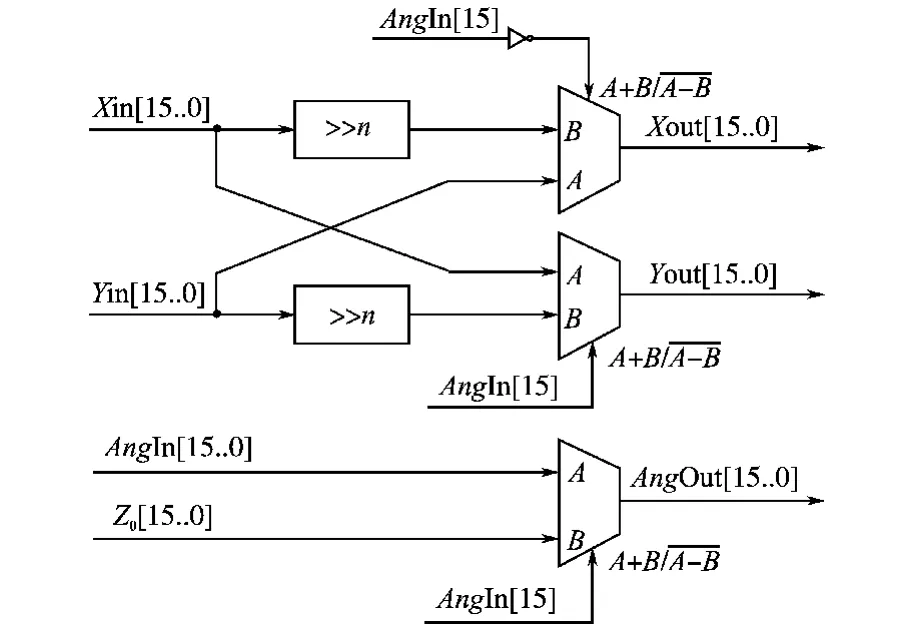
图5 CORDIC迭代结构Fig.5 Iterative CORDIC structure

文中选用Altera公司Cyclone III系列FPGA和12位高速AD转换器，根据图4设计了硬件电路，对HEIDEHAINN公司一款编码器输出的正余弦信号做了1 024细分，细分效果如图6所示。其中D＿A为采集到的正弦波，Position为细分后的数据，从Position［9］到Position［0］依次是1，2，4，8，16，32，64，128，512，1 024细 分。 从图6中可以看出1 024细分波形清晰，达到了预期的效果。

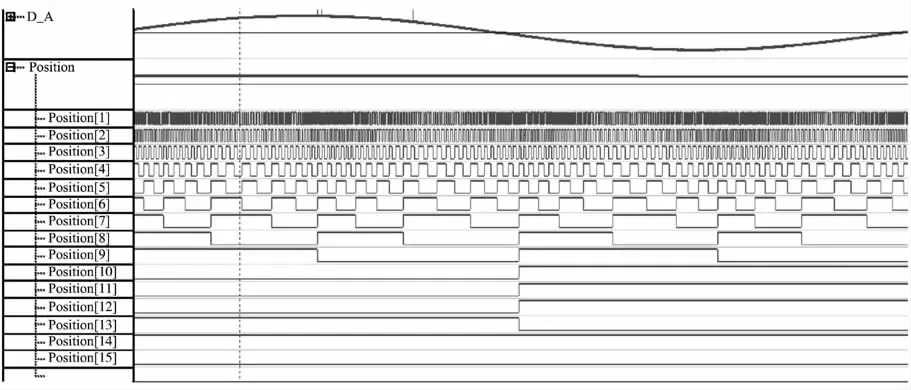
图6 跟踪环路细分实验结果Fig.6 Subdivision experimental results of tracking－loop

4 结论

正余弦信号输出的位置检测元件通常用在高精度运动控制中做位置和速度反馈，通过对正余弦信号细分可以提高位置检测精度。文中分析了传统的正余弦编码器信号细分方法，针对传统电阻链细分法细分数低，细分硬件复杂，开环细分方法中粗精结合跳变沿不同和开环细分滤波难度大的问题，提出了一种基于跟踪环路的细分方法并对跟踪环路细分方法原理做了详细介绍，分析了固有频率和阻尼系数对控制环路的影响，并且采用通用模拟器件和FPGA搭建了硬件平台实现了CORDIC算法和PI控制器模块，对跟踪环路细分做了验证。实验结果证明，这种细分方法可满足高精度角度控制要求。

［1］Krah J O，Schmirgel H.FPGA Based Sine－cosine Encoder Feedback Processing for Servo Drive Applications［C］∥International Exhibition ＆Conference for Power Electronics Intelligent Motion Power Quality 2007.Nuremberg，Germany：Mesago PCIM GmbH，2007：1－6.

［2］张善锺.计量光栅技术［M］.北京：机械工业出版社，1985.

［3］张国雄，金篆芷.测控电路［M］.北京：机械工业出版社，2005.

［4］史敬灼，王秀丽，徐殿国.交流伺服系统光电编码器信号处理电路设计与实现［J］.微特电机，2007，35（11）：18－19.

［5］隋继平.高速正余弦细分装置［P］.CN 101729071A，2010.

［6］卢少武，唐小琦，马泽龙，等.CORDIC算法在光栅莫尔条纹细分中的应用［J］.自动化仪表，2010，31（5）：23－25.

［7］常海涛，叶孝佑，孙双花，等.基于FPGA的正交信号细分系统研究［J］.计量学报，2008，29（4A）：36－39.

［8］喻洪麟，黄良明，王远干.莫尔条纹信号的DSP滤波及细分技术研究［J］.光电工程，2004，9：61－65.

［9］Andraka R.A Survey of CORDIC Algorithms for FPGA Based Computers［C］∥FPGA1998.ACM／SIGDA International Symposium on Field Programmable Gate Arrays.Monterey，CA，USA：ACM，1998.