分布式风力发电对综合负荷特性的影响

唐 捷，肖园园，李欣然，张元胜，4

（1.广东电网公司 韶关供电局，广东 韶关 512026；2.湖南大学 电气与信息工程学院，湖南 长沙 410082；3.广西电力科学研究院，广西 南宁 530023；4.广西电力调度通信中心，广西 南宁 530023）

发展可再生能源尤其是风能发电被视作解决能源紧缺问题、促进低碳环保经济的重要方案，风力发电已成为世界上增长最快的新能源［1］.过去5年中，全球累计风电装机增长率达27.09%，新增装机容量增长率达35.48%［2］，中国的风电装机总容量和2011年新增装机容量更是位居世界第一.

风能发电主要有2种基本开发模式：①集中式——百万甚至千万kW级大规模风电场以220 kV及以上电压等级直接并入主网；②分散式——万kW级小容量风电场接入110kV及以下电压等级配网.在分散式情形下，风力发电作为分布式电源接入配网，必然改变传统的综合负荷特性，使之成为一种“广义负荷”［3－4］.随着分布式风力发电并网容量的增加，渗透率逐步增大，对配电网区域综合负荷特性的影响不可忽视，研究此种条件下的负荷建模方法、评估分布式风力发电对负荷特性的影响规律及影响程度，负荷建模必须解决理论与实际工程问题.文献［3］阐述了电源接入配网后对负荷模型的影响，其仿真研究结果表明：当配网电源容量比例大于24.4%后，感应电动机并联ZIP模型描述能力具有局限性，由此提出异步电机并联ZIP模型的广义负荷模型结构；文献［4］在分析电源对广义电力负荷建模影响的基础上，给出了3种广义电力负荷模型，并给出了模型参数的辨识策略；文献［5］的研究结果表明：将传统的CLM或SLM模型中的负荷动静比例系数km的取值由［0，1］扩大为任意实数，可以实现对含分布式风力发电的广义负荷特性的准确描述；文献［6］分析了不同渗透率下微电网对电压稳定和攻角稳定的影响，为分布式发电优化并网提供理论依据；文献［7］在考虑风力发电特点的基础上，对含风电的电网进行规划，建立相应的节能和风电利用指标对规划模型进行评价.

笔者将以 Matlab/Simpowersystem仿真系统为研究工具，将风力发电以不同容量比例接入配网中的不同并网母线，系统而定量地评估分布式风力发电的接入位置和并网容量对配网侧综合负荷特性的影响.

在数理统计学中的数值相似性与趋势相似性的概念，多用于在统计学及经济性中分析2组数据之间的相似程度及规律，在电力系统仿真领域已有学者将其用于电力系统的仿真分析及相关的模型评估［8］.文献［9－10］利用相似性判断原理通过对实测和仿真序列的相似程度来判断模型的准确度；文献［11］利用PSS/E软件结合实测数据的混合仿真以评估某局部电网的元件模型是否准确.上述文献都很好地利用了数值与变化趋势相似性的概念，比较2组数据之间的关系.笔者利用文献中对仿真模型分析的方法，对不同接入方式下的风机并网后综合母线功率曲线进行两两比较，最终得到各曲线之间的相似关系及变化规律.

1 仿真方案

风力发电作为分布式电源接入系统后，对负荷特性影响的主要因素为并网时接入容量与接入点地理位置.为此，首先须制定合理的仿真方案.笔者制定了具体仿真方案与仿真方法.

1）选用具有一定典型代表意义的IEEE－14节点配电网络作为仿真研究对象，其结构如图1所示.

图1 IEEE－14节点配网结构Figure 1 The IEEE－14node distribution network structure

仿真系统中，节点1是220kV主网等值系统（无穷大系统）的220kV枢纽变电站的10kV母线，为14节点配网与主网间的公共连接界面，也即“配网侧综合负荷母线”；接于母线1的配电网即为研究对象，其通过220kV变压器从主网获得的下网负荷即为“配网侧综合负荷”.配网总额定负荷为28.7＋j7.75MV·A，支路A负荷为8.5＋j4.65 MV·A，支路B负荷为15.1＋j1.4MV·A，支路C负荷为5.1＋j1.7MV·A［12］.各节点负荷均采用感应电动机并联ZIP的综合负荷，并依据IEEE－14节点网络各类负荷典型参数对网络进行设置.

2）当配电网中不接入任何分布式电源时（即纯负荷），在10kV母线上设置持续0.2s的三相短路故障，导致故障母线电压跌落近20%（为方便分析，下文所涉及到的仿真全部是此相同故障）.以故障发生时刻为计时起点（t＝0），测量故障后暂态过程中的综合母线负荷特性数据.此为不含分布式电源的原始态网络数据.

3）考虑风机不同接入方式.设置风机容量为总负荷容量的10%～80%，将风机分别接到节点2，3，4，5，7（其中节点2，3，4分别为不同类型的负荷支路上的共点节点，节点2，5，7分别为同一支路的首、中、末端），测量暂态过程中的综合负荷母线动态数据.此仿真网络除风机接入的容量及位置变化外，其他条件均与原始态一致.

根据所提仿真方案在IEEE－14网络中依次进行仿真，采集综合母线点吸收有功的仿真测量数据，并进行功率平移，将功率以各自稳态值为基准进行量化归一化［13］后观察，如图2所示（以节点2对应的8种容量组为例）.

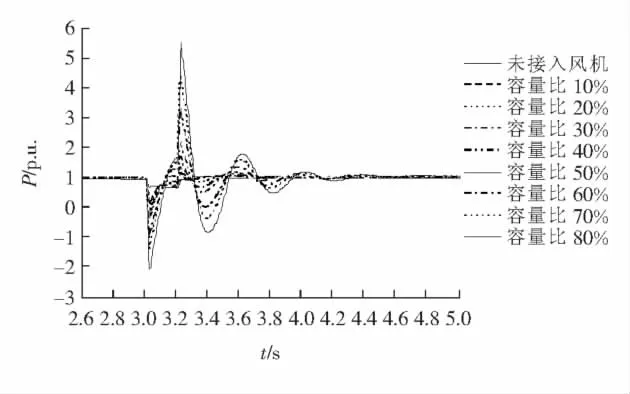
图2 不同容量风机接入节点2时综合母线功率情况Figure 2 Comprehensive bus power when turbine connecting to the node2with different capacity

由图2可看出，当风电机组按照不同的容量比例依次接在节点2位置上时，综合母线的有功吸收量随风电源投入量呈现递增规律性，在暂态尤为明显.而风电源接在配网中距离综合母线不同位置的节点上时，有功是否也存在规律性呢？笔者为此找寻方法分析在风电不同接入方式下对配电网综合负荷特性的影响.就负荷特性而言，通常有功功率响应处于主动和主导地位，且无功功率响应受补偿因素影响较大而不一定能客观反映负荷特性的内在本质特征.因此，笔者采用综合负荷的有功响应作为分析对象以考察负荷特性的差异（或相似）性.

2 基本思路与分析方法

为分析分布式风力发电电源按照不同容量和不同地点接入配电网对配网侧综合负荷特性的影响，笔者采用递进关系的层次步骤分析方法，选择合适的对象进行分析.一般而言，可以将一个动态系统受扰动后的暂态过程分为前稳态、暂态、后暂态、后稳态4个阶段，如图3所示.

图3 暂态过程分解及其暂态特征参数示意Figure 3 Transient process and transient feature parameters

显然，系统的暂态响应是其动态特性的直观反映；不同系统（或同一系统在不同条件下）之暂态响应的差异（或相似）程度，即反映了其内在特性的差异（或相似）程度.系统动态特性的差异程度可用不同的指标测度.显然，暂态过程持续时间以及相对于稳态响应的暂态偏移量可以作为描述暂态程度的重要指标［14］.据此，定义4个“暂态特征参数”以刻画暂态过程中的负荷动态特性的变化程度，其物理意义如图3所示.其中：

暂态时间t1——受扰动后的直至功率跃变到最大时的暂态过程持续时间；

调节时间t2——故障清除到恢复稳态的后暂态时间；

有功跃变量ΔP1——故障开始时有功功率的跃变值；

有功超调量ΔP2——功率波动最大值与后稳态功率的差值.

由上述定义可知，4个暂态特征参数分别从不同角度刻画了负荷动态特性的差异性.应当指出，实际应用时，暂态特征参数之t1，t2用实际有名时间（s）；跃变量ΔP1和超调量ΔP2用相对值表示，其定义由公式给出，即

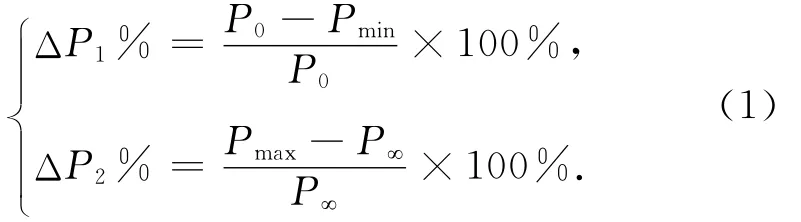
式中 P0，P∞，Pmin，Pmax依次为扰动前稳态有功功率、暂态过程结束后的稳态有功功率、暂态过程中有功功率达到的最小值和最大值.

由于分布式风电对综合负荷特性的主要影响因素为其接入容量及接入地理位置，因此为进行定量分析，必须有具体的评价指标.笔者引用数理统计学中数据处理及误差分析的相关理论原则，定义“特征差异度”评价指标.

3 特征差异度分析方法

1）特征差异度的定义.

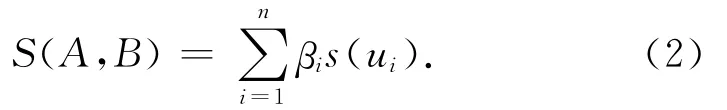
设数据组A的数值为Yr，数据组B为Ys，则相似元的值为s（ui）：

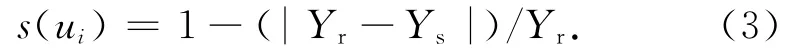
由相似元的定义可知，相似差异度越大，则说明2组数据之间的差别越大.因此，根据所提的4种暂态特征参数，将暂态时间t1、调节时间t2、跃变量ΔP1、超调量ΔP2分别作为对应相似元素，从而得到对应的相似差异值，笔者即将此差异值定义为“特征差异度”.

2）相似元权重系数.

系统分析人员对暂态过程中每个阶段的仿真结果的看重程度不一样，且各阶段对影响分析的重要程度也不同，通常更关心在暂态过程中功率的跃变及故障撤离后功率的恢复过程，因此，需先给暂态过程中各不同的观察点赋予一个权重值.权重系数可采用层次分析法（Analytic Hierarchy Process，AHP）来确定［15］.层次分析法的一个重要特点是用两两重要程度之比的形式表示出各单元的相应重要性程度等级.设n个相似元分别为U＝｛u1，u2，…，ui，…un｝，i＝1，2，…，n，j＝1，2，…，n.根据数值权重标度及定义，按两两相比较的结果构成判断矩阵：

其中 uij表示ui对uj的相对重要性程度，一般若ui与uj同等影响程度，则权重标度值为1；若ui比uj稍显重要，则标度值为3；若ui比uj明显重要，则标度值为5；若相似元ui比uj强烈重要，则标度值为7，以此类推.在该判断矩阵A中，有uij＞0，uⅡ＝1，uij＝1/uji，由于A为正互反矩阵，且若为一致性矩阵，则对于任意的i，j能满足uij＝uik×ukj，故先假设矩阵A满足一致性，再确定权重β，得到权重数组.确定权重系数数组步骤如下.

步骤1：将矩阵A各元素进行列向量归一，即得列权重向量

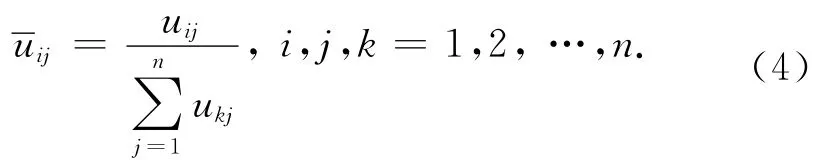
步骤2：将第1步归一化后得到的列权重向量按行相加，得每行权重向量

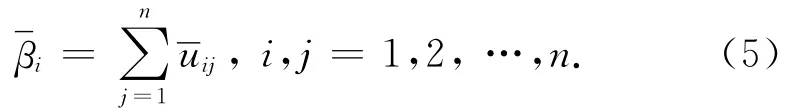
步骤3：将第2步所得权重向量进行规范归一化处理相加，得权重数组

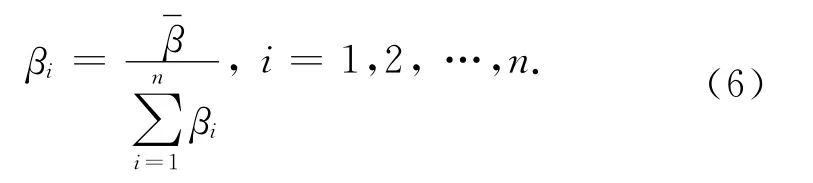
在实际应用中，由于判断矩阵的权重标度的选定一般是根据专家经验或者实验情况分析得来，当判断矩阵的阶数大于2时，构造出来的矩阵通常难以满足一致性要求，为此，需要对判断矩阵是否可以满足一致性进行检验.由一致性检验的内涵可知，对于正互反矩阵A，当且仅当A为一致性矩阵时，其最大特征根λmax≥n成立，其中n为矩阵A的阶数，定义一致性指标CI和平均一致性指标［15］，即

平均一致性指标RI是指在判断矩阵阶数较多时，即存在多个相似元的情况下，重复进行随机判断矩阵特征值的计算平均得到.随机一致性比率是指矩阵的一致性指标CI与同阶次的平均随机一致性指标RI的比值CR决定，当CR＜0.1时，则认为矩阵满足一致性［14］.

为进行具体差异性分析，需确定各相似元的权重系数，根据文中对权重系数的定义及相应暂态特征参数的重要程度，得到判断矩阵：

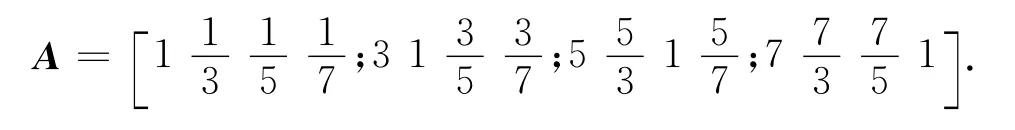
由该矩阵可得其最大特征根为λmax＝4，一致性指标CI＝0，查表得平均随机一致性指标RI（4）＝0.90，所以一致性指标CR＝0＜0.1，故认为该判断矩阵满足一致性.进一步根据上文所提到的计算方法，得到t1，t2，ΔP1，ΔP2对应的权重系数：

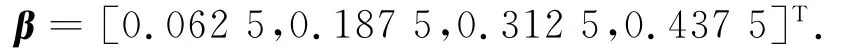
4 接入方式对负荷特性影响性分析

根据上文关于特征差异度与权重系数的定义方法，结合将风电源在IEEE－14节点网络中以不同容量大小分别接入不同地理位置的情况，采集在相同故障条件综合负荷母线点的有功功率，从暂态时间t1、调节时间t2、跃变量ΔP1、超调量ΔP2等4个角度对有功进行观测并分析其对配网负荷特性的影响程度.由第1节设定的仿真方案可知，当风力发电系统容量以10%～80%的比例分别在节点2，3，4，5，7节点时，对应将有40组数据，因此与原始态进行两两比较时，数据涵盖信息丰富.为更好地分析这些数据组之间的趋势关系，笔者分别从3种不同的比较方案选定基准数据，通过式（3）的差值计算后确定3种方案的相似元.

比较方案1 以原始态数据为基准，以不同接入方式下的有功数据作为参比量进行差值计算；

比较方案2 以接入量占总负荷比例10%的分布式电源的有功数据为基准，以递增容量下的数据进行参比差值计算；

比较方案3 由图2可以看出，在各节点上，当每增加10%的风机容量投入时，功率在暂态的增值也有一定的增大趋势，因此，比较每增加10%容量比例风机容量时，相邻2组容量下的有功差值得出有功的变化规律.

分别将40组分布式风电按不同方式接入后的负荷特性数据及原始态数据进行比较，依据上文定义的特征差异度的计算方法，得到对应的特征差异度.限于篇幅，以图形化表现如图4所示.

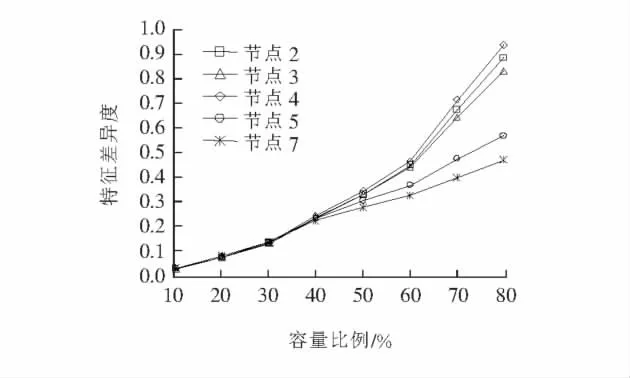
图4 方案1各接入方案特征差异度Figure 4 Characteristic difference degree of scheme 1

3种比较方案中，通过选择不同的比较基准，从暂态过程中的4个角度，结合相似性分析的概念，对不同比较方案下的数据组进行了差值对比及相似计算.

方案1中在与不加任何分布式风电源之间进行有功功率的暂态相似性比较时，可见在每个节点位置下，当接入容量递增时，特征差异度值都呈递增的趋势，说明随着容量的增加，综合母线节点的暂态变化呈递增趋势，即风机容量的增加对综合母线负荷特性的影响逐步增强，且在接入容量小于40%时，由于分布式电源比例较小，当接在配网中不同位置时，相对于综合母线点来说差别不大；且由图4可知，当容量投入量超过40%后，曲线上升率明显增强，可得出结论，即风力电源接入容量越大时，对负荷特性的影响越为明显；从5个节点的角度观察，当分别接入不同支路的首段时（节点2，3，4），随着接入点所在支路负荷越大（支路B＞支路A＞支路C），差异值越小，即对综合负荷特性影响越弱；当分别接入同一支路的首、中、末端时（节点2，5，7），随着距离综合母线点越远，差异值越小，即对负荷特性影响越小，此结论与综合残差影响分析方法所得保持一致.

由于方案1的比较是与原始态进行比较，而原始态配网中为纯感应电机并联ZIP静态负荷，无功率流出，因此，与加入分布式风电时相比差别较大，因此在方案2中，以接入风机10%容量比下的综合母线点暂态数据为比较基准，将20%～80%容量比下的7组暂态数据分别与之进行比较，相对于方案1来说，比较更精确，差值更小.且由图5可见，其趋势规律与方案1相当，更证明了方案1所得结论的正确性.

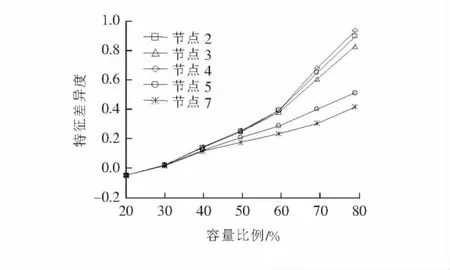
图5 方案2各接入方案特征差异度Figure 5 Characteristic difference degree of scheme 2

方案3的比较方式较为特别，即将各节点8种容量比下的暂态有功进行归一化后，两两暂态功率之间的差值（即容量比例20%～10%，30%～20%，…，80%～70%）进行特征差异性比较分析.在仿真实测数据中，之所以在每增加10%容量的风机投入时，功率暂态之间会呈现一定的差值，这是由于风机作为发电机存在于配网中，而配网负荷吸收功率，因此，每投入一定容量的风机于配网中，必然会对综合母线点的功率有所影响.而由图6各差值之间比较结果可知，在相同容量增量下，不同节点下的影响基本一致；在较大的基准值上增加10%容量时，影响略增大，但趋势基本平稳相当，说明增加等量的风机投入时，对负荷特性的影响基本呈线性趋势.

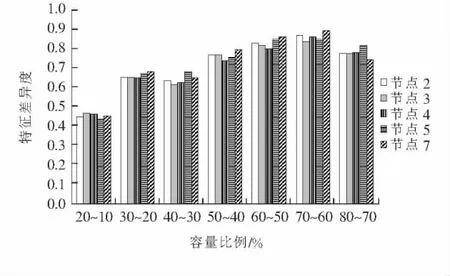
图6 方案3各接入方案特征差异度Figure 6 Characteristic difference degree of scheme 3

5 结语

随着分布式发电技术应用规模的日益扩大，定量准确地评估分布式电源对所接入配网的广义负荷特性的影响，对于负荷建模研究及其工程应用具有重要意义.笔者以分布式发电的影响为研究对象，定义“特征差异度”以衡量分布式风力发电对负荷特性的影响程度，实现其客观定量评估.研究结果表明：分布式风力发电对负荷特性的影响程度，随着其并网点距综合母线距离的增加而减小，随着并网容量比例的增大而增大，二者影响程度的相对大小与并网点所在供电回路负荷水平有关.尤其值得注意的是：接入容量越大，大扰动下的负荷暂态响应过程的功率跃变幅度以及故障切除后的稳态恢复时间显著增加.

笔者所提出的定量指标对于评估其他分布式电源对负荷特性的影响具有借鉴意义.

［1］马志博，刘友波.英国风电发展及其调度概述［J］.电力科学与技术学报，2011，26（1）：53－59.MA Zhi－bo，LIU You－bo.Review of wind power development and dispatching experience in the UK［J］.Journal of Electric Power Science and Technology，2011，26（1）：53－59.

［2］罗如意，林晔，钱野.世界风电产业发展综述［J］.可再生能源，2010，28（2）：14－17.LUO Ru－yi，LIN Ye，QIAN Ye.The development and prospects of world wind power industry［J］.Renewable Energy Resources，2010，28（2）：14－17.

［3］王吉利，贺仁睦，马进.配网侧接入电源对负荷建模的影响［J］.电力系统自动化，2007，31（20）：22－26.WANG Ji－li，HE Ren－mu，MA Jin.Impact of connecting power sources on load modeling in a distribution network［J］.Automation of Electric Power System，2007，31（20）：22－26.

［4］鞠平，何孝军，黄丽，等.广义电力负荷的模型结构与参数确定［J］.电力系统自动化，2006，30（23）：11－13.JU Ping，HE Xiao－jun，HUANG Li，et al.Model structures and parameter estimation of generalized loads［J］.Automation of Electric Power System，2006，30（23）：11－13.

［5］李欣然，惠金华，钱军，等.风力发电对配网侧负荷建模的影响［J］.电力系统自动化，2009，33（13）：89－94.LI Xin－ran，HUI Jin－hua，QIAN Jun，et al.Impact of wind power generation on load modeling of distribution network［J］.Automation of Electric Power System，2009，33（13）：89－94.

［6］张佳佳，陈金富，范荣奇.微网高渗透对电网稳定性的影响分析［J］.电力科学与技术学报，2009，24（1）：25－29.ZHANG Jia－jia，CHEN Jin－fu，FAN Rong－qi.Investigation of the influence of microgrids high large penetration ratios on power network stability［J］.Journal of Electric Power Science and Technology，2009，24（1）：25－29.

［7］高赐威，何叶.考虑风力发电接入的电网规划［J］.电力科学与技术学报，2009，24（4）：19－24.GAO Ci－wei，HE Ye.Research of electric network planning with wind power integration considered［J］.Journal of Electric Power Science and Technology，2009，24（4）：19－24.

［8］周成，贺仁睦，王吉利，等.电力系统元件模型仿真准确度评估［J］.电网技术，2009，33（14）：12－15.ZHOU Cheng，HE Ren－mu，WANG Ji－li，et al.Assessment on simulation accuracy of power system component models［J］.Power System Technology，2009，33（14）：12－15.

［9］柳世考，刘兴堂，张文.利用相似度对仿真系统可信度进行定量评估［J］.系统仿真学报，2002，14（2）：143－145.LIU Shi－kao，LIU Xing－tang，ZHANG Wen.Fixed quantity evaluation to reliability of simulation system with similar degree［J］.Acta Simulata Systematica Sinica，2002，14（2）：143－145.

［10］焦鹏，唐见兵，查亚兵.仿真可信度评估中相似度方法的改进及其应用［J］.系统仿真学报，2007，19（12）：2 658－2 660.JIAO Peng，TANG Jian－bing，ZHA Ya－bing.Amelioration and application of similar degree method for simulation credibility evaluation［J］.Acta Simulata Systematica Sinica，2007，19（12）：2 658－2 660.

［11］马进，盛文进，贺仁睦，等.基于广域测量系统的电力系统动态仿真验证策略［J］.电力系统自动化，2007，31（18）：11－15.MA Jin，SHENG Wen－jin，HE Ren－mu，et al.A simulation validation strategy based on wide area measurement［J］.Automation of Electric Power Systems，2007，31（18）：11－15.

［12］钱军.考虑分布式发电的配电网综合负荷建模方法研究［D］.长沙：湖南大学，2009.

［13］崔凯，房大中，钟德成.电力系统暂态稳定性概率评估方法研究［J］.电网技术，2005，29（1）：44－49.CUI Kai，FANG Da－zhong，ZHONG De－cheng..Study on probabilistic assessment method for power system transient stability［J］.Power System Technology，2005，29（1）：44－49.

［14］周成，贺仁睦.电力系统仿真模型有效性的动态评估［J］.电网技术，2010，34（3）：61－64.ZHOU Cheng，HE Ren－mu.Dynamic evaluation of effectiveness of power system simulation models［J］.Power System Technology，2010，34（3）：61－64.

［15］储敏.层次分析法中判断矩阵的构造问题［D］.南京：南京理工大学，2005.